Opengl图形几何变换的模式

当我们对一个图形进行一个较为复杂的变换时，我们并不直接去计算这个变换，而是将其分解为多个基本变换，再依次作用于图形。对于复合变换：

$$ P^{,} = M_{n} \cdots M_{3} \bullet M_{2} \bullet M_{1} \bullet P$$

先作用的变换放在连乘式右边，后作用的变换放在连乘式左边。由于矩阵乘法不满足交换律，因此变换合成矩阵的顺序不同，产生的结果也不同。

 

1. 固定坐标系模式

在变换合成或者复合变换时，先调用的变换先执行，后调用的变换后执行，体现在矩阵相乘时，先调用的变换矩阵放在连乘式的右边，后调用的变换放在连乘式的左边。这种变换模式成为固定坐标模式，也称为图形模式。他的特点是在连续执行几次变换时，每一次变换均可看成相对于原始（固定）坐标系进行的。

（1）先把图形绕z轴旋转90度，然后再平移距离7.

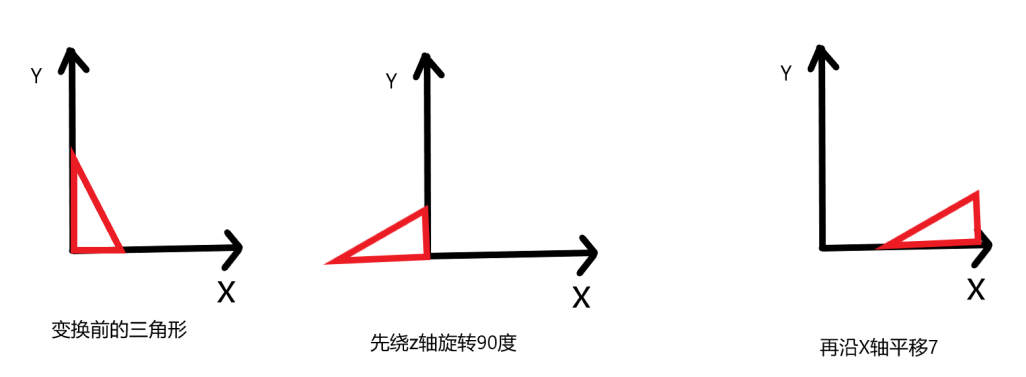
（2）先把图形沿x轴平移7，再绕z轴旋转90度。

显然，两种变换方案的结果不同，但都是相对于原坐标oxy坐标系进行的，先调用的变换先执行。

 

2.活动坐标系模式

活动坐标系模式，又称空间模式。在这种模式下，连续执行几个变换时，变换矩阵的合并方式恰好和固定坐标系模式相反。即先调用的变换在连乘式的左边，后调用的变换在连乘式的右边。体现在程序执行上，先调用的变换后执行，后调用的变换先执行，它非常适合堆栈结构实现，也是OpenGL图形库采用的方式。

我们重新来考虑上面的两种变换。

（1）将图形与坐标系一起旋转90度；在新坐标系中，将图形与坐标系一起沿x轴平移7.

图形在它局部坐标系中的位置是不变的，这样变换事实上是作用于坐标系而非图形本身。

（2）将图形与坐标系沿x轴平移7；再将图形与坐标系一起旋转90度。

 

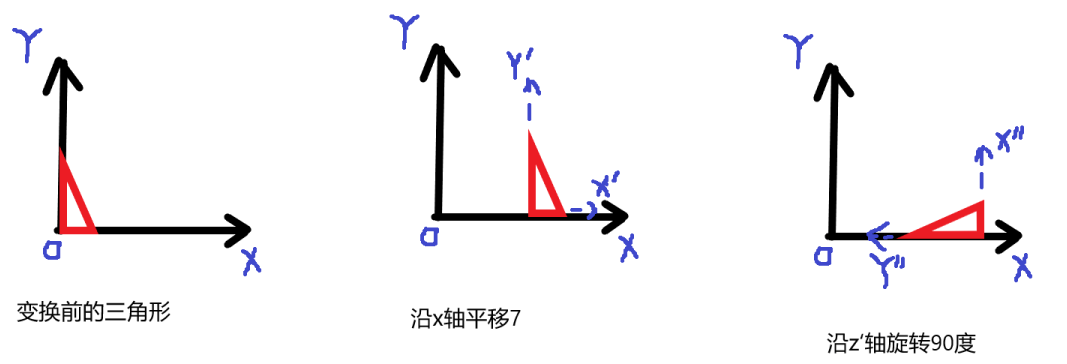
我们使用程序来看一下效果。

首先我们画一个三角形。

    float vertices[] = {
        //位置坐标      颜色属性
        0.0, 0.0, 0.0, 1.0, 0.0, 0.0,
        0.1, 0.0, 0.0, 1.0, 0.0, 0.0, 
        0.0, 0.2, 0.0, 1.0, 0.0, 0.0
    };

我们看一下原始图形：

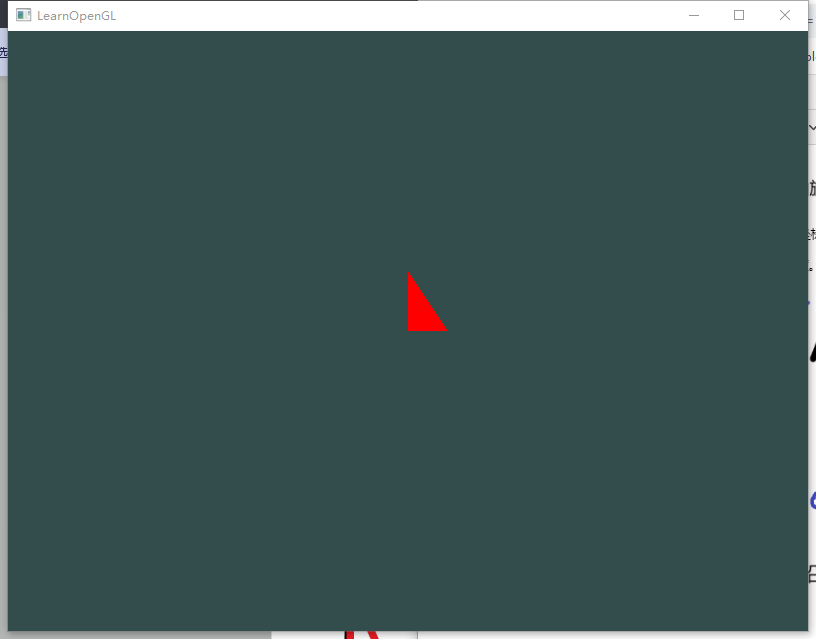
（1）首先我们绕Z轴旋转90度，然后再沿X平移0.5：

    glm::mat4 transform(1.0f);
    transform = glm::rotate(transform, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0f));
    transform = glm::translate(transform, glm::vec3(0.5, 0, 0));
    ourShader.use();
    ourShader.setMat4("transform", transform);

（2）先沿x轴平移0.5，再沿z轴旋转90度：

glm::mat4 transform(1.0f);
transform = glm::translate(transform, glm::vec3(0.5, 0, 0));
transform = glm::rotate(transform, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0f));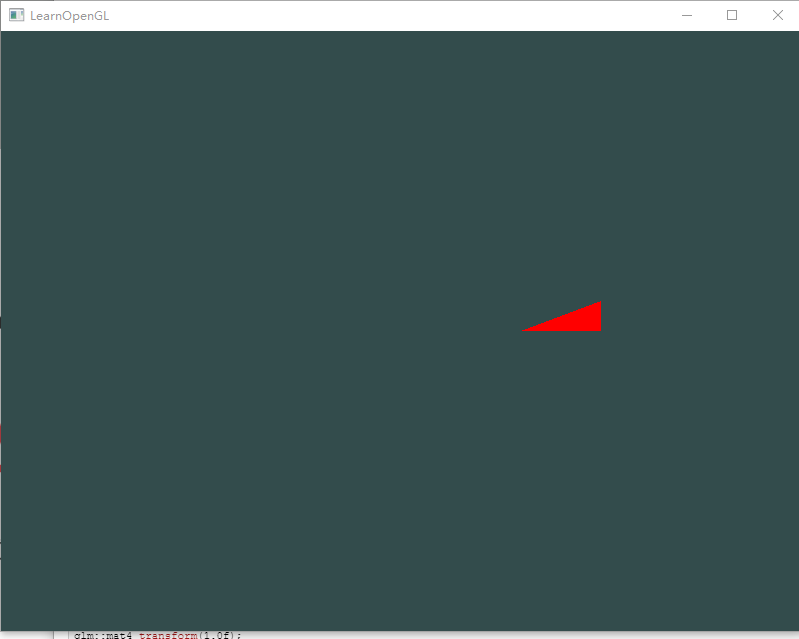

从两个不同的结果看出，opengl使用的是活动坐标系，其实是对图形的局部坐标系进行的变换。

 

不同的应用要用不同的变换模式。在绘图的情况下多用固定坐标系模式，因为比较容易估计变换后的后果。整体变换的基础上再作一些较为独立的局部变换时，常用活动坐标系模式。例如机械手变换到适当位置后，手腕和手指的运动是相对于手臂的，如果在手臂上建立一个坐标系，那么手指手腕的运动就简单多了。