对主定理(Master Theorem)的理解

前言

虽说在学OI的时候学到了非常多的有递归结构的算法或方法，也很清楚他们的复杂度，但更多时候只是能够大概脑补这些方法为什么是这个复杂度，而从未从定理的角度去严格证明他们。因此借着这个机会把主定理整个梳理一遍。

介绍

主定理（Master Theorem)提供了用于分析一类有递归结构算法时间复杂度的方法。这种递归算法通常有这样的结构：

def solve(problem):
    solve_without_recursion()
    for subProblem in problem:
        solve(subProblem)

我们可以用一种表示方式来概括这些结构的算法：对于一个规模为\(n\)的问题，我们把它分为\(a\)个子问题，每个子问题规模为\(\frac nb\)。那么这种方法的复杂度\(T(n)\)可以表示为：

\[T(n)=a\,T\Big(\frac nb\Big)+f(n) \]

其中\(a\ge 1,b>1\)为常数，\(\frac{n}{b}\)指\(\lfloor \frac{n}{b}\rfloor\)或\(\lceil \frac{n}{b}\rceil\)，\(f(n)\)为创造这些递归或者将这些子问题结果整合的函数。对这个方法我们可以建一个递归树：

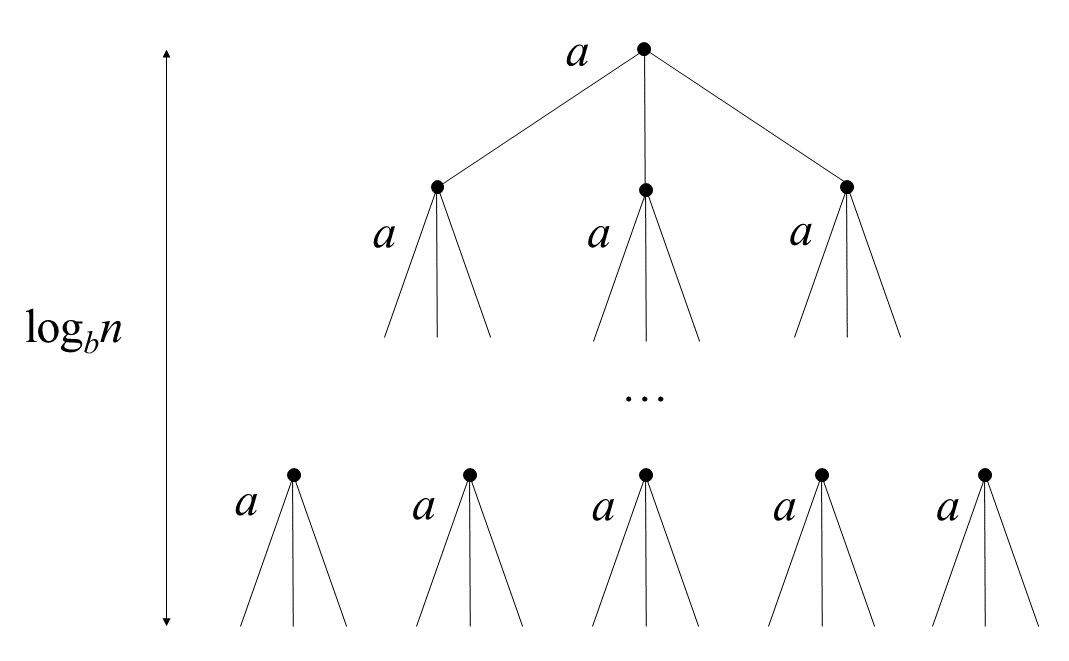
其中树高为\(\log_bn\)，树的第\(i\)层有\(a^i\)个节点，每个节点的问题规模为\(\frac{n}{b^i}\)。则这棵树有\(a^{\log_bn}=n^{\log_ba}\)个叶子节点。因此这种方法的复杂度也可以表示为：

\[T(n)=\Theta(n^{\log_ba})+\sum_{i=0}^{\log_bn-1}a^if\Big(\frac{n}{b^i}\Big) \]

从中我们可以看出，整个方法的复杂度取决于\(f(n)\)的复杂度。主定理对\(f(n)\)分了三种情况：

1. \(\exist \varepsilon>0\ s.t.\ f(n)=O(n^{\log_ba-\varepsilon})\)。此时\(T(n)=\Theta(n^{\log_ba})\)。
2. \(f(n)=\Theta(n^{\log_ba})\)。此时\(T(n)=\Theta(n^{\log_ba}\lg n)\)。
3. \(\exist \varepsilon>0\ s.t.\ f(n)=\Omega(n^{\log_ba+\varepsilon})\)，且\(\exist c<1\)，当\(n\)足够大时，有\(a\, f(\frac{n}{b})\le c\, f(n)\)。此时\(T(n)=\Theta(f(n))\)。

\(f(n)\)含\(\log\)的情况类似，待补充。

证明

Case 1

令\(g(n)=\sum_{i=0}^{\log_bn-1}a^if(\frac{n}{b^i})\)，由\(f(n)=O(n^{\log_ba-\varepsilon})\)，得：

\[g(n)=O\Big(\sum_{i=0}^{\log_bn-1}a^i\Big(\frac{n}{b^i}\Big)^{\log_ba-\varepsilon}\Big) \]

之后就是对后面式子的化简：

\[\begin{aligned} \sum_{i=0}^{\log_bn-1}a^i\Big(\frac{n}{b^i}\Big)^{\log_ba-\varepsilon} &= n^{\log_ba-\varepsilon}\sum_{i=0}^{\log_bn-1}\Big(\frac{ab^\varepsilon}{b^{\log_ba}}\Big)^i\\ &= n^{\log_ba-\varepsilon}\sum_{i=0}^{\log_bn-1}(b^\varepsilon)^i\\ &= n^{\log_ba-\varepsilon}\Big(\frac{(b^\varepsilon)^{\log_bn}-1}{b^\varepsilon-1}\Big)^i\\ &= n^{\log_ba-\varepsilon}\Big(\frac{n^\varepsilon-1}{b^\varepsilon-1}\Big)^i \end{aligned} \]

因此\(g(n)=O(\sum_{i=0}^{\log_bn-1}a^i(\frac{n}{b^i})^{\log_ba-\varepsilon})=O(n^{\log_ba})\)。所以有：

\[T(n)=\Theta(n^{\log_ba})+O(n^{\log_ba})=\Theta(n^{\log_ba}) \]

Case 2

同Case 1。令\(g(n)=\sum_{i=0}^{\log_bn-1}a^if(\frac{n}{b^i})\)得：

\[g(n)=\Theta\Big(\sum_{i=0}^{\log_bn-1}a^i\Big(\frac{n}{b^i}\Big)^{\log_ba}\Big) \]

继续化简：

\[\begin{aligned} \sum_{i=0}^{\log_bn-1}a^i\Big(\frac{n}{b^i}\Big)^{\log_ba} &= n^{\log_ba}\sum_{i=0}^{\log_bn-1}\Big(\frac{a}{b^{\log_ba}}\Big)^i\\ &= n^{\log_ba}\log_bn \end{aligned} \]

因此可得\(g(n)=n^{\log_ba}\log_bn=n^{\log_ba}\lg n\)。所以有：

\[T(n)= \Theta(n^{\log_ba})+\Theta(n^{\log_ba}\lg n)=\Theta(n^{\log_ba}\lg n) \]

Case 3

还是令\(g(n)=\sum_{i=0}^{\log_bn-1}a^if(\frac{n}{b^i})\)。但Case 3这里有一个条件：\(a\, f(\frac{n}{b})\le c\, f(n)\)。我们对这个条件做一下处理：

\[\begin{aligned} a\, f\Big(\frac{n}{b}\Big) &\le c\, f(n)\\ \Rightarrow f\Big(\frac{n}{b}\Big) &\le \frac{c}{a}f(n)\\ \Rightarrow f\Big(\frac{n}{b^2}\Big) &\le \frac{c}{a}f\Big(\frac nb\Big)\le\Big(\frac{c}{a}\Big)^2f(n)\\ &\vdots\\ f\Big(\frac{n}{b^i}\Big) &\le\Big(\frac{c}{a}\Big)^if(n)\\ \Rightarrow a^i\, f\Big(\frac{n}{b^i}\Big) &\le c^i\, f(n)\\ \end{aligned} \]

由此我们可以很轻易的向下化简：

\[\begin{aligned} \sum_{i=0}^{\log_bn-1}a^i\Big(\frac{n}{b^i}\Big)^{\log_ba} &\le \sum_{i=0}^{\log_bn-1}c^i\,f(n)+O(1)\\ &\le f(n)\sum_{i=0}c^i+O(1)\\ &=f(n)\Big(\frac{1}{1-c}\Big)+O(1)\\ &=f(n) \end{aligned} \]

得\(g(n)=O(f(n))\)。又因为\(g(n)=\sum_{i=0}^{\log_bn-1}a^if(\frac{n}{b^i})\ge f(n)\)，得\(g(n)=\Omega(f(n))\)。因此\(g(n)=\Theta(f(n))\)。
所以有：

\[T(n)=\Theta(n^{\log_ba})+\Theta(f(n))=\Theta(f(n)) \]

证毕。

应用

二叉树建树

\[T(n)=2T\Big(\frac{n}{2}\Big)+O(1),\ T(n)=O(n) \]

此时\(\log_ba<1\)，满足Case 1。

BFPRT(Median of Medians)

\[T(n)\le T\Big(\frac{n}{5}\Big)+\Big(\frac{7n}{10}\Big)+O(n),\ T(n)=O(n) \]

此时\(\log_ba>1\)，即划分之后总规模减小（\(1/5+7/10<1\)），满足Case 2。

归并排序

\[T(n)=2T\Big(\frac{n}{2}\Big)+O(n),\ T(n)=O(\lg n) \]

此时\(\log_ba=1\)，满足Case 3。