浅谈伸展树
みなさん、こんにちは。今天我们来讲解伸展树。
0.原题
(来自LuoGu P3369 【模板】普通平衡树)
题目描述
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
插入 x 数
删除 x 数(若有多个相同的数,因只删除一个)
查询 x 数的排名(排名定义为比当前数小的数的个数 +1 )
查询排名为 x 的数
求 x 的前驱(前驱定义为小于 x,且最大的数)
求 x 的后继(后继定义为大于 x,且最小的数)
输入格式
第一行为 n,表示操作的个数,下面 n 行每行有两个数 opt 和 x 表示操作的序号( 1≤opt≤6 )
输出格式
对于操作 3,4,5,6 每行输出一个数,表示对应答案
输入输出样例
输入 #1
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
输出 #1
106465
84185
492737
说明/提示
【数据范围】
对于 100% 的数据, 1≤n≤105,∣x∣≤107 。
1.分析
Q1:我们需要那些准备呢?
A1:编程基础的语法,二分答案的思想(二叉搜索树)和手写4K的勇气。(别怕,怕你就输了)
Q2:我们需要用什么算法?
A2:没错,就是标题——伸展树。至于为什么叫Splay,个人理解是这样的。
Q3:Splay的思想是什么?
A3:当然是伸展啦。qwq
Q4:Splay一下子学不会怎么办?
A4:正常,请保持耐心,本人打了5遍的Splay还可以打出WA和TLE。我在学Splay的时候适当的背了一点代码(因为有些代码真的较难理解)。
01).定义重要
#include<bits/stdc++.h>
#define Root T[0].Ch[1]//Root为0结点的右儿子(左儿子也没事,但后面代码的时候稍微注意一下)
struct Floor{//用T来表示伸展树结点的基本信息
int Val;//结点的值
int Fa;//结点的父亲
int Ch[2];//结点的左右儿子
int Size;//以此结点为根的子树的大小
int Recy;//关键,结点的重复次数
}T[MAXN];
int N;//操作个数
int NodeNum;//申请的结点个数
int TSize;//伸展树的大小
02).更新函数(Update)
void Update(int X){
T[X].Size=T[T[X].Ch[0]].Size+T[T[X].Ch[1]].Size+T[X].Recy;//当前的结点为根的子树大小为左右儿子的大小加上自己的重复次数
}
03).父子关系函数(Relation)
int Relation(int X){//求X为它父亲的什么儿子(左/右)
return T[T[X].Fa].Ch[0]==X? 0:1;//0为左儿子,1为右儿子
}
04).连接函数(Connect)
void Connect(int X,int Y,int Son){//Y当父亲,X当儿子,Son表示X要成为Y的什么儿子(左/右)(千万别把第三个参数忘记)
T[X].Fa=Y;//X认Y做父亲
T[Y].Ch[Son]=X;//Y认X做(左/右)儿子
}
05).旋转函数(Rotate)关键
我相信许多同学(包括我自己),都被旋转搞晕过。其实这都要靠套路。
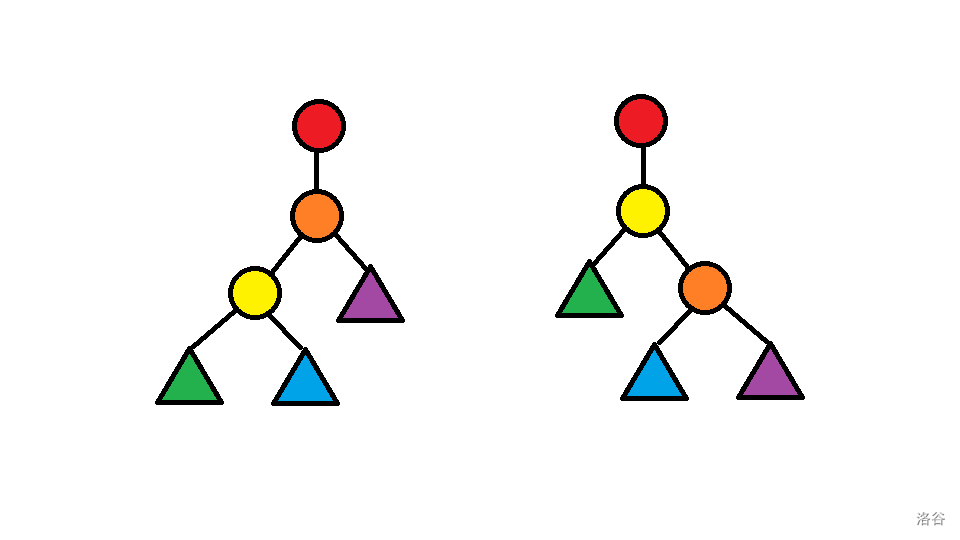
我们旋转的时候是以黄色作为我们的旋转点的。
而我们的目标是让黄色上去。
观察如上图片,我们可以发现,只有结点红,橙,黄,蓝的父子关系发生变化。只有结点橙,黄的Size发生变化。
我们看到,蓝色的位置是处于黄色与橙色相夹的位置,一旦黄色向上旋转,必然从黄色的左(右)儿子变成橙色的右(左)儿子。
第一步,我们先让黄色把蓝色吸过来,吸过来占据原来黄色在橙色当儿子的位置。
然后我们要把黄色转上去,所以让黄色吸来占据原来蓝色在黄色当儿子的位置。
最后,我们要让红色认黄色这个儿子,所以让黄色来占据原来橙色在红色当儿子的位置。
这就是旋转三板斧,理清楚之后就非常的简单了。
void Rotate(int X){
int Y=T[X].Fa;
int YSon=Relation(X);
int R=T[Y].Fa;
int RSon=Relation(Y);
int XSon=YSon^1;
int B=T[X].Ch[XSon];
Connect(B,Y,YSon);//旋转三板斧
Connect(Y,X,XSon);
Connect(X,R,RSon);
Update(Y);//别忘了哦
Update(X);
}
06).伸展函数(Splay)关键
伸展树最关键的来啦
我们在旋转伸展树时,会有一些结点深度变浅,但是也会有一些结点深度变深。貌似双旋可以让树的深度更加平均。
void Splay(int From,int To){//表示结点From转到To的位置
To=T[To].Fa;//问题交给大家Q5:为什么要写这一步
while(T[From].Fa!=To){//如果From未到To
int Up=T[From].Fa;
if(T[Up].Fa==To){
Rotate(From);
}else if(Relation(Up)==Relation(From)){
Rotate(Up);
Rotate(From);
}else{
Rotate(From);
Rotate(From);
}
}
}
A5->Q5:当From为To的儿子时,Rotate操作会把To给转下去。
07).查找结点函数(Find)
int Find(int Value){
int Now=Root;//从根节点开始
while(Now){//Now=0表示没有这个结点了
if(Value==T[Now].Val){
Splay(Now,Root);//这一步千万别忘,不然会像我一样光荣WA
return Now;//返回结点编号
}
int Next=Value<T[Now].Val? 0:1;//Q6:这一步能看懂吗
Now=T[Now].Ch[Next];
}
return 0;
}
A6->Q6:如果Value<T[Now].Val就往左走,否则往右走。如果忘了,可以翻上去再看一下 1).定义哦。
08).创造结点(CreNode)
void CreNode(int Value,int Father){
NodeNum++;//结点数量加1
T[NodeNum].Fa=Father;//认父亲
T[NodeNum].Val=Value;//赋值
T[NodeNum].Size=T[NodeNum].Recy=1;//注意:不要忘记给Recy赋值为1哦
}
09).创造结点(Insert)重要
int Insert(int Value){
if(TSize==0){
TSize++;
Root=NodeNum+1;//别忘这一步!!!
CreNode(Value,0);//创造结点
return NodeNum;//Q7:返回值,至于为什么返回,下一个函数解答
}else{
TSize++;
int Now=Root;//从根节点开始
while(1){
T[Now].Size++;//别忘这一步,每一次Now走到的地方必然是新加结点的长辈或是它自己
if(Value==T[Now].Val){//如果找到值一样的,就Recy加一
T[Now].Recy++;
return Now;//返回结点编号
}
int Next=Value<T[Now].Val? 0:1;//还记得Q6吗,现在理解了吗,如果没有,就再向前翻一下 07).查找结点函数
if(!T[Now].Ch[Next]){//发现不存在结点
T[Now].Ch[Next]=NodeNum+1;//这一步别忘,父子关系要认清
CreNode(Value,Now);//创造结点
return NodeNum;//返回结点编号
}
Now=T[Now].Ch[Next];//移动Now
}
}
}
10).创造结点(Push)
void Push(int Value){
int AddNode=Insert(Value);
Splay(AddNode,Root);
}
A7->Q7:别忘了还要Splay呀。当然也可以不写这个函数,直接用Splay(NodeNum,Root);代替09).创造结点的return NodeNum;
11).破坏结点(Destroy)
void Destroy(int X){
T[X].Val=T[X].Fa=T[X].Ch[0]=T[X].Ch[1]=T[X].Size=T[X].Recy=0;//完全把这个结点去除
}
12).破坏结点(Pop)重要
void Pop(int Value){
int KillNode=Find(Value);//还记得Find里面有一句Splay(Now,Root);所以现在KillNode是整个伸展树的根,或没有这个结点
if(!KillNode) return;//没有这个结点就退
TSize--;//别忘记把整个树的大小减一
if(T[KillNode].Recy>1){//
T[KillNode].Recy--;
T[KillNode].Size--;//别漏哦,X的Size是它左右儿子的Size加上Recy。如果忘了,可以向前翻 02).更新函数
return;
}
if(!T[KillNode].Ch[0]){如果没有左子树,直接右子树的根代替
Root=T[KillNode].Ch[1];
T[Root].Fa=0;//别漏哦,父子关系要认清
}else{//如果有左子树
int LMAX=T[KillNode].Ch[0];//在左子树找最大的结点来代替
while(T[LMAX].Ch[1]){
LMAX=T[LMAX].Ch[1];
}
Splay(LMAX,T[KillNode].Ch[0]);//把它转到左子树的根
int R=T[KillNode].Ch[1];//右子树的根
Connect(R,LMAX,1);//连接,R是LMAX的右儿子
Connect(LMAX,0,1);//连接,如果最开始写Root为T[0].Ch[0],这边就写Connect(LMAX,0,0);
Update(LMAX);//这一步也别忘记
}
Destroy(KillNode);//破坏这个结点
}
13).查找值为X的排名(Rank)困难
int Rank(int Value){
int Now=Root;//从根开始
int Ans=1;//它应该至少是第一名吧
while(Now){
if(Value==T[Now].Val){//找到了
Ans=Ans+T[T[Now].Ch[0]].Size;//别忘这一步,它会大于左边的所有结点值
Splay(Now,Root);//旋转到根上
return Ans;//返回排名
}else
if(Value<T[Now].Val){//向左
Now=T[Now].Ch[0];
}else
if(Value>T[Now].Val){//向右
Ans=Ans+T[T[Now].Ch[0]].Size+T[Now].Recy;//关键,向右时Ans要加上左边的Size和当前的Recy,Q8:为什么要这么加?
Now=T[Now].Ch[1];
}
}
return 0;
}
A8->Q8:因为根据二叉排序树的性质,如果Value>T[Now].Val,它会大于所有左边的结点值,同时也大于T[X].Recy所代表的值。
14).查找排名为X的值(Atrank)困难
int Atrank(int X){
if(X>TSize){//如果排名大于整个树的大小,就意味着没有这个值
return 0;
}
int Now=Root;//从根开始
while(Now){
if(T[T[Now].Ch[0]].Size<X && X<=T[Now].Size-T[T[Now].Ch[1]].Size){//解释:T[Now].Size-T[T[Now].Ch[1]].Size等同于T[T[Now].Ch[0]].Size+T[Now].Recy表示小于等于T[Now].Val的结点总个数。Q9:为什么这么比较
Splay(Now,Root);//旋转到根
return T[Now].Val;//返回结点值
}
if(X<=T[T[Now].Ch[0]].Size){//比左边的Size还要小,就往左走
Now=T[Now].Ch[0];
}else
if(T[Now].Size-T[T[Now].Ch[1]].Size<X){//翻译:排名X的值比T[Now].Val大,则向右走
X=X-(T[Now].Size-T[T[Now].Ch[1]].Size);//一定要减,千万别忘
Now=T[Now].Ch[1];
}
}
}
A9->Q9:因为X大于当前左子树的所有值,但X小于等于小于等于T[Now].Val的结点总个数。所以X的值就是T[Now].Val。(这个是真的难讲,如果真的不会,可以先暂时背一下代码)
15).查找值为X的前驱(Lower)(与13相似)
int Lower(int Value){
int Now=Root;
int Ans=-INF;//找最大值,Ans为负无穷
while(Now){
if(Value>T[Now].Val && T[Now].Val>Ans){//符合比Value小,而且比当前答案大,就更新
Ans=T[Now].Val;
}
if(Value>T[Now].Val){//重要,这容易写错。如果Value==T[Now].Val,就要向左走
Now=T[Now].Ch[1];
}else
if(Value<=T[Now].Val){
Now=T[Now].Ch[0];
}
}
return Ans;//返回前驱
}
16).查找值为X的后继(Upper)(与12相似)
int Upper(int Value){
int Now=Root;
int Ans=INF;//找最小值,Ans为正无穷
while(Now){
if(Value<T[Now].Val && T[Now].Val<Ans){//符合比Value大,而且比当前答案小,就更新
Ans=T[Now].Val;
}
if(Value<T[Now].Val){//重要,这容易写错。如果Value==T[Now].Val,就要向右走
Now=T[Now].Ch[0];
}else
if(Value>=T[Now].Val){
Now=T[Now].Ch[1];
}
}
return Ans;//返回后继
}
17).主程序(Main)
int main(){
scanf("%d",&N);//输入N
while(N--){
scanf("%d%d",&Opt,&X);//输入指令和值
if(Opt==1){//分指令进行操作
Push(X);//添加结点操作。
}else if(Opt==2){
Pop(X);//删除结点操作。
}else if(Opt==3){
printf("%d\n",Rank(X));//输出值为X的排名。
}else if(Opt==4){
printf("%d\n",Atrank(X));//输出第X小的数。
}else if(Opt==5){
printf("%d\n",Lower(X));//输出值为X的前驱。
}else{
printf("%d\n",Upper(X));//输出值为X的后继。
}
}
return 0;//结束
}
悄悄说一句话,把上面所有的代码拼接起来就可以过洛谷平衡树模板题。


