线性代数学习笔记(十二)
即使是实数矩阵,其特征值也可能为复数。所以我们也需要考虑矩阵元素为复数的情况。
复数
以下各小节可概括为一句话:将复数向量/矩阵转置时,记得同时对其取共轭!
向量的模长平方
假如向量z=[z1 z2 ... zn]T, 每个分量都可能是复数,那么\( \left \| z \right \| ^2 \) 就不再是zTz,而是\( \bar{z}^Tz \)。
“共轭再转置”有个简化标记:\( \bar{z}^T=z^H \),H表示Hermitian
Review:在复平面上理解复数a和复数b相乘,结果的模长是a和b模长的乘积,结果的角度是a和b角度之和。当a与b共轭时,角度正好为2pi。
向量的内积
和模长类似,向量y 与 向量x 的内积=\( \bar{y}^Tx = y^Hx \)
Note:内积的结果有可能是复数(但模长只能为实数)。
复数矩阵的对称性
为什么要定义对称复数矩阵?我们希望对称矩阵的特性(1.特征值都是实数;2. 特征向量互相垂直)在复数矩阵上也成立。
在证明对称矩阵的特征值都是实数时,关键一步是:\( \bar{x}^TAx=\bar{x}^T\lambda x=\bar{x}^T\bar{A}^Tx \)(参见上一节笔记),我们需要 \( A=\bar{A}^T=A^H \)才能保证复数矩阵特征值依然为实数。
因此,复数矩阵的对称性:\( A=\bar{A}^T=A^H \),可知主对角线必为实数,且对称元素共轭。这和直观感觉的不是很一样,比如下面这个复数矩阵是对称的(感受一下):
\( \begin{bmatrix}2 & 3-3i\\ 3+3i & 5\end{bmatrix} \)
酉矩阵(Unitary Matrix)
实对称矩阵的特征向量相互垂直,将所有单位特征向量按列向量拼凑,得到正交矩阵Q,有:\( Q^TQ=I \)
复对称矩阵的(复数)特征向量也相互垂直,其单位特征向量组成的正交矩阵(称之为酉矩阵)Q,有:\( \bar{Q}^TQ=Q^HQ=I \)
PS:第一次见到“酉”这么奇怪的翻译,百度为什么这么翻译得到的结果是:“酉”是Unitary的音译,据说是华罗庚的建议。中英文都有“一”和“元”的意思。
傅里叶变换
傅里叶矩阵
形式见下,并且满足:
- \( w^N=1 \),也就是:
![\omega]() 是1的
是1的![n]() 次方根的主值(primitive nth root of unity),大小为
次方根的主值(primitive nth root of unity),大小为![\exp(-2\pi i/N)]() ,这里这个负号是依据惯例加的
,这里这个负号是依据惯例加的 - 将矩阵除以根号下N是依据惯例而加,目的是将列向量的模长变成1,从而成为单位正交基

- 这个矩阵在传统意义上对称,但不是Hermitian对称(1.主对角线元素不是实数;2.共轭转置不等于原矩阵)。
- 但是,这个矩阵是酉矩阵(unitary matrix),其不同列的列向量内积=0,也就是WHW=I(待解决:为什么W的列向量是一组正交基?)
- 由上可知,WT=WH,也就是 傅里叶逆矩阵 同样具有 傅里叶矩阵 的性质(什么性质?似乎就是:1. 列是基;2. 可用FFT)
快速傅里叶变换(Fast Fourier Transform)
我们需要将F或者F-1与向量相乘,常规方法需要n2次乘法,FFT利用矩阵的周期性,将复杂度降为O(n*log n),这个方法加速了众多工业领域的运算。
FFT的关键在于下面这个分解:

这部分讲的比较简略,没涉及到具体的例子,理解复杂度和应用还需要深入进去。BTW傅里叶变换在网易上也有一门专门的公开课。



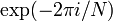 ,这里这个负号是依据惯例加的
,这里这个负号是依据惯例加的

 浙公网安备 33010602011771号
浙公网安备 33010602011771号