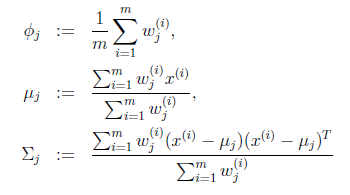哲学与算法——高斯混合模型算法

GMM这是图像处理，模式识别和深度学习领域一个百嚼不烂的话题。很多人被一堆数学公式，迭代求和和看似毫无联系的likehood EM算法搞得糊里糊涂。

其实就算羡慕着很多牛气哄哄的学霸炫耀公式推理的IT普工们，我们有没有问过自己，我们真的知道GMM吗？于是有些人和我一样有了如下的思考和疑问：

1.到底什么是高斯混合模型？最好能一句话或者简单的话说明白，至少让我一辈子也忘不掉这个该死的算法。。。

2.GMM是如此复杂有效，能让GMM算法向富士康的iphone流水线一样，虽然精密庞杂但却能完整直观的展现在我们面前吗？

3.可以再详细一点吗？

4.为什么会有这个算法模型？GMM存在的意义是什么，能解决什么问题？

5.GMM真的是万能的吗？它有什么问题，我如何避免或修正他们？

6.。。。。

为了彻底解决这些看似简单原生态的问题，我拜读了很多大牛的文章，写了代码做了实验，只为一睹GMM芳颜：

1.到底什么是高斯混合模型？最好能一句话或者简单的话说明白，至少让我一辈子也忘不掉这个该死的算法。。。

一句话，就一句话：GMM——道生一一生二二生三三生万物。（我相信很多中国人，至今都不会断句这句话。。。）

是的，我说GMM来自与哲学，而老子则直接告诉你他就是"道"。GMM是人们认识自然万物相生相克的规律，是大脑对自然认识后的长时间归纳与沉淀。GMM的核心思想就是任意的形态（不管是可见的光，图像，还是抽象的多维度变量模型，比如经济金融危机模型），都来可以用高斯核函数来累积加权得到，经管这些核可能不止一个，有不同的维度，不一的中心，甚至相差很大的波动。这都不妨碍他们谦卑的遵循高斯概率模型的函数性质，都能分解成为那个迷人的公式：

公式（1）

再后来我们拥有了计算机，而且当离散数学这一学科方法的出现，连续Gauss模型要完成计算机的模拟，所以离散化的概率密度函数就表示成这样了：

公式（2）

相信这里学渣们又开始烦了，神马意思？又一坨！

相信我，这是你后面降妖除魔的朱砂，就算你不认同这坨东东，那我告诉你，即使他是一坨，那也是一坨可遇不可求的『狗黄金』，只能这样解释了，我已词尽xx!

解释一下，x是样本变量，p(x)是样本之与你大GMM模型的概率（真实的叫法是概率密度，其实概率即是概率密度的积累积分，打住，渣爷们，这个括号你当没看见），K是你要最终分的类别个数（这个有讲究，后书分解），很多paper里讲K is compenents of GMM。后面的是指x由第k个高斯模型生成的概率，那么是什么？paper中多叫『reponse matrix』,我们叫他第k类的权重，就是这个高斯model在所有model里的对样本x属于k类的一个贡献大小，简单讲就是江湖里老k入会时的股份，以后牛叉了，股份可以增加哦。。。，接下来，就是那句名言：有人的地方就是江湖。苦逼的GMM为了形成强大的黑客帝国，不断迭代进步，这一的进步的同时，各帮派的上位斗争也开始惊心动魄地上演：

1）对于GMM最终的那个强大model来说，我不关心你们的争斗，只要你们都能上交最多的利润p(x)，我就高兴（这里就是gmm的一个bug，paper上叫局部最优缺陷），如果各帮派能在自己最大利润的情况下，和谐相处达到平衡，那就最好不过了，说明老大的公司已经开启印钞模式，走上迎娶白富美的大道啦。。。于是，江湖规矩变因运而生！！！

公式（3），但是老大是台machine啊，离散的p(xi)是很小的，计算机无法存储有些太小的浮点值，怎么办？数学就像股票界的"狗庄"一样，猥琐的出现了——Log()函数！又一幕气死学渣，乐死学霸的戏剧上演了。于是规矩就成了：

公式（4），其实我可以再详细一点的，否则学霸要鄙视了，

于是规矩终归这里（Champions belong to here eventually）：

公式（5），这里的N(xxx)函数就是上面的概率密度的数学规范表示。这就是大名鼎鼎的log-likehood function，如果能求出他，找到最大值，那么这时对应的高斯模型就是最终的模型，每个model对样本的作用加权出的p(xi)自然就可以完成分类（这里涉及一个量化标准，自己找paper，到这个时候还敢做『伸手党』，估计你是到不了双十一了，直接剁了双爪，哈哈）。下面的核心任务就是最精彩的空手套白狼的游戏了——如何解出这个最大似然函数，揭开屌丝们朝思暮想的GMM妹妹真容了！

至此，第一个问题算是憋完了，各位就这么看吧！再说，估计得便秘了。。。

 

2.GMM是如此复杂有效，能让GMM算法向富士康的iphone流水线一样，虽然精密庞杂但却能完整直观的展现在我们面前吗？

我想说：能！大部分说GMM复杂，无非是因为怕公式，不明所以。不是庖丁，不知牛之大概，牛何解邪？要有个直观的呈现，无非就是要准备的了输入，下得去流水线，搞懂制造工艺流程，最后还能装箱出厂，完成iphone般高大上的输出。那么接下来就让我们看看GMM算法的整个工序流程:

首先是训练样本N个，每个样本xi中含有D维的变量，最终想要分到K个结果类中，每个维度变量对应上面概率密度函数中的一个均值中心u，和一个该高斯核生成这个xi的"模型权重wi"。用矩阵表示应该更易理解：样本X（N*D），均值U（D*K），权重wi（N*K）.这是第一步输入问题和输入的简单矩阵模型，下面就是到底要最什么？这个问题在问题1中有讲诉，就是求能使GMM模型达到利益最大化的那个max likehood function的极值。

于是第二步制造工艺就是求极值，众所周知求极值，那肯定是要用到导数啦，但是你仔细翻翻高数的课本，你会发现maxlikehood function与课本里乘积的概率形式又有些差别，好像总差点什么，没关系让数学来做，既然求导复杂难度大，不利于计算设计解耦，那么是否有另外的解决方法？真有，EM算法！（渣爷们估计又一片骂声。。。）ok，我来解释一下，为什么想到EM，这得从EM的本质和特点来讲，EM来自与假设验证的收敛思想。讲简单一点就是，如果一个来源与真实情况（你可以理解为来自真实样本）的假设，只要有个验证模型（我们这里就是指高斯模型）存在，我就可以验证你刚才的假设与模型的输出结果的差异，然后再通过这个差异来建立新的假设，再输入模型继续验证。当你连续的假设差异（这里应该准确的讲是正向差异）足够小时，是否意味着这时的假设和模型的吻合度足够高？系统足够稳定？当然！

这里其实有些坑，比如我的验证模型为什么是高斯，其实只要能证明模型在你关心的中心附近收敛，波动有限，你也可以选取。

由于这种收敛和验证都是来源与样本假设，那问题来了，这种假设是否真的准确？答案是否定的，你EM得到的稳定模型只是个局部样本最优。为什么，原因很简单：你的样本是抽样采集的，你无法保证你的实验样本（海中一粟）能反应真实事件的各种复杂情况，最大的保证只能说尽量代表真实情况。

那么问题又来了，我如何保证我的样本，如果没有办法，那GMM就没有应用价值了？答案是有的，还记得你信号与系统中不起眼的地方有个抽样定理吗？抽样的频率要至少为样本频率的2倍，否则采样结果不能保证反应样本的主要信息。

so，。。。这个你该懂了吧。

3.可以再详细一点吗？（学覇自动忽略这一节，这是抽取JerryLead大神的思路说给学渣听的，谢谢~）

天空飘来8个字：秒杀学霸不是事儿！当然可以，学渣们现在开始——带你装逼带你飞！

大EM算法：前面做了一个逻辑分析，为什么引入EM算法来求极值。其实这是缺少数学论证的，本身就是一种假设上的假设验证，因此有必要从数学角度来论证这个问题确实可以用数学的方法去解决。

首先，你要理解一些数学概念，比如jensen不等式（凹函数f(E(x))>=E[f(x)]），高数上的凹凸函数(log是一个凹函数)。现在我们可以把maxlikehood函数写的更数学一些，这里就是做了个空手用来套『白狼』，这个空手就是隐含类别z,这是个什么东东？在数学上我们认为它也是各分布，只不过是简单的多项式分布，就是为了描述某个样本样列xi属于类k的表示，就是zi=k,就是上面说的wi=p(zi=j|xi,u,sigma,类权重)，就是满足『样列属于类k的一个权重』。这里有个逻辑要说一下，只有我们确定了这个隐含分类zi（空手）之后，我们的样列xi才能说符合某个高斯分布，即。由此可以得到联合分布，看到没这就是公式（2）。（这里有些数学条件限制，后面附上链接，各位愿意了解的可以仔细看看JerryLead的推导，这里只做必要解释）ok，下面再对maxlikehood function做细化：

公式（6）

这时候就是Jenssen和log凹函数的作用了，上面的公式就变成了这样：

公式（7）log()移到了里面，乘积被分解为和。

这个时候对上式分布求导，对和进行求导得到：

公式（8），下面解释一下：

第一个就是我们上面问题里的Wk，不是wi。上面3各公式，分别表示类j的权重，中心，与方差波动。OK，至此一个EM循环就over了。

最后大牛jerryLead的一张图来显示一下EM loop：

循环下面步骤，直到收敛： {

      （E步）对于每一个i和j，计算

                  

      （M步），更新参数：

                  

}

这里不想再贴别人的图了，因为我觉得该解释的地方都解释了。。。。，再说，估计学霸们要说我恶心抄袭了（虽然只是几个占地方的公式，但确实对不住JerryLead大神，愿神保佑！哈哈）

至此GMM算法就抡完了。。。。下面是一些提后话

4.为什么会有这个算法模型？GMM存在的意义是什么，能解决什么问题？

1）前面这个问题，有点扯，真的，就像你问为什么有人类一样？而且我也并不想像学霸那样翻历史书，告诉你在xxx时间背景下，他就诞生了！

当你看到了一下现象，认识一下事物，特别是一些人后，我们总按照千百年的进化惯性，去有意无意的分解总结事物，以期望认识新的事物。比如你认识阳光，你又用三棱镜分解了他成不同频率的七色光，然后你有用计算机模拟出组成他们的RGB三原色。于是一天你看到了一种从未见过的花，你会很自信的说我可以把它的颜色存储下来。但是事实上事物中蕴含太多的未知，只是鉴于人类对未来的恐惧的一种惯性反应——分解它，用最小的元素去理解他，这样你就不会害怕。。。。

2）GMM的意义，在于我们可以尝试用一种正态分布的模型去模拟一些独立元素组成的事物与其事物的区别。

就比如在米缸里找出大豆一样，但前提是这两者用可量化的不同，比如形状，密度。。。。

5.GMM真的是万能的吗？它有什么问题，我如何避免或修正他们？

1）前面其实都有提到，比如极值的局部最优问题？模型的个数真的就只需要compent个吗？，输入的样本维度如果不独立怎么办（估计上帝都不敢肯定这个问题）？

2）避免和修正：可以用有监督学习来初始化zi，可以尽量提高采样频率，可以量化样本维度，可以改进输出量化方法。。。。等等。。。

6.感谢很多愿意分享的人，下面附录一下我还记得和参考过的大神blog：

1）http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html

2）http://blog.csdn.net/zouxy09/article/details/9982495

3）。。。对不起忘记了。。。。

也许精彩才刚刚开始。。。。