关于凸包算法
前言
今日的困难题,属于会凸包算法就可套模板,不会凸包算法自己不容易推出来的类型。
所以借此机会补一下凸包算法。
凸包简介

计算凸包的算法
Jarvis算法
基本思想:首先必须要从凸包上的某一点开始,比如从给定点集中最左边的点开始,例如最左的一点 A1。然后选择 A2点使得所有点都在向量 A1A2的左方或者右方,我们每次选择左方,需要比较所有点以 A1为原点的极坐标角度。然后以 A2为原点,重复这个步骤,依次找到 A3,A4,…,Ak。
具体实现:给定原点 p,如何找到点 qq,满足其余的点 r 均在向量 pq的左边,我们使用「向量叉积」来进行判别。
- 我们可以知道两个向量 pq、qr的叉积大于 0 时,则两个向量之间的夹角小于 180°,两个向量之间构成的旋转方向为逆时针,此时可以知道 r一定在 pq的左边;
- 叉积等于 0 时,则表示两个向量之间平行,p,q,r在同一条直线上;
- 叉积小于 0 时,则表示两个向量之间的夹角大于 180°,两个向量之间构成的旋转方向为顺时针,此时可以知道 r 一定在 pq的右边。
为了找到点 q,我们使用函数 cross() ,这个函数有 3 个参数,分别是当前凸包上的点 p,下一个会加到凸包里的点 q,其他点空间内的任何一个点 r,通过计算向量 pq,qr的叉积来判断旋转方向,如果剩余所有的点 r均满足在向量 pq的左边,则此时我们将 q加入凸包中。要注意共线的情况。
复杂度分析:
- 时间复杂度:O(n2)
- 空间复杂度:O(n)
1 class Solution { 2 public: 3 //计算向量叉积 4 int cross(vector<int>p,vector<int>q,vector<int>r){ 5 return (q[0]-p[0])*(r[1]-q[1])-(q[1]-p[1])*(r[0]-q[0]); 6 } 7 vector<vector<int>> outerTrees(vector<vector<int>>& trees) { 8 int n=trees.size(); 9 if(n<4) 10 return trees; 11 int leftMost=0; 12 for(int i=0;i<n;i++){ 13 if(trees[i][0]<trees[leftMost][0]) 14 leftMost=i; 15 } 16 vector<vector<int> >result; 17 vector<bool>visited(n,false); 18 int p=leftMost; 19 do { 20 int q=(p+1)%n; 21 //找到此时边上的 22 for(int r=0;r<n;r++){ 23 if(cross(trees[p],trees[q],trees[r])<0) 24 q=r; 25 } 26 //寻找同一条线上的 27 for(int i=0;i<n;i++){ 28 if(visited[i]||i==p||i==q) 29 continue; 30 if(cross(trees[p],trees[q],trees[i])==0){ 31 result.push_back(trees[i]); 32 visited[i]=true; 33 } 34 } 35 if(!visited[q]){ 36 result.push_back(trees[q]); 37 visited[q]=true; 38 } 39 p=q; 40 } while(p!=leftMost); 41 return result; 42 } 43 };
Graham算法
基本思想:首先选择一个凸包上的初始点 bottom。我们选择 y坐标最小的点为起始点,我们可以肯定 bottom一定在凸包上,将给定点集按照相对的以 bottom为原点的极角大小进行排序。
具体实现:函数 cross。极角顺序更小的点排在数组的前面。如果有两个点相对于点 bottom的极角大小相同,则按照与点 bottom的距离排序。我们还需要考虑另一种重要的情况,如果共线的点在凸壳的最后一条边上,我们需要从距离初始点最远的点开始考虑起。所以在将数组排序后,我们从尾开始遍历有序数组并将共线且朝有序数组尾部的点反转顺序,因为这些点是形成凸壳过程中尾部的点,所以在经过了这些处理以后,我们得到了求凸壳时正确的点的顺序。
现在我们从有序数组最开始两个点开始考虑。我们将这条线上的点放入栈中。然后我们从第三个点开始遍历有序数组 trees。如果当前点与栈顶的点相比前一条线是一个「左拐」或者是同一条线段上,我们都将当前点添加到栈顶,表示这个点暂时被添加到凸壳上。
检查左拐或者右拐使用的还是 cross函数。对于向量 pq,qr,计算向量的叉积 cross(p,q,r)=pq×qr
- 如果叉积小于 0,可以知道向量 pq,qr顺时针旋转,则此时向右拐;
- 如果叉积大于 0,可以知道向量 pq,qr逆时针旋转,表示是左拐;
- 如果叉积等于 0,则 p,q,r在同一条直线上。
如果当前点与上一条线之间的关系是右拐的,说明上一个点不应该被包括在凸壳里,因为它在边界的里面,所以我们将它从栈中弹出并考虑倒数第二条线的方向。重复这一过程,弹栈的操作会一直进行,直到我们当前点在凸壳中出现了右拐。这表示这时凸壳中只包括边界上的点而不包括边界以内的点。在所有点被遍历了一遍以后,栈中的点就是构成凸壳的点。
复杂度分析:
- 时间复杂度:O(nlogn),
首先需要对数组进行排序,时间复杂度为 O(nlogn),每次添加栈中添加元素后,判断新加入的元素是否在凸包上,因此每个元素都可能进行入栈与出栈一次,最多需要的时间复杂度为 O(2n),因此总的时间复杂度为 O(nlogn)。
- 空间复杂度:O(n)
1 class Solution { 2 public: 3 //计算向量叉积 4 int cross(vector<int>p,vector<int>q,vector<int>r){ 5 return (q[0]-p[0])*(r[1]-q[1])-(q[1]-p[1])*(r[0]-q[0]); 6 } 7 //计算向量距离 8 int distance(vector<int>p,vector<int>q){ 9 return (q[0]-p[0])*(q[0]-p[0])+(q[1]-p[1])*(q[1]-p[1]); 10 } 11 vector<vector<int>> outerTrees(vector<vector<int>>& trees) { 12 int n=trees.size(); 13 if(n<4) 14 return trees; 15 int bottom=0; 16 for(int i=1;i<n;i++){ 17 if(trees[i][1]<trees[bottom][1]) 18 bottom=i; 19 } 20 swap(trees[bottom],trees[0]); 21 //以bottom为原点,按照极坐标的极角大小进行排序 22 sort(trees.begin()+1,trees.end(),[&](const vector<int>&a,const vector<int>&b){ 23 int diff=cross(trees[0],a,b)-cross(trees[0],b,a); 24 if(diff==0) 25 return distance(trees[0],a)<distance(trees[0],b); 26 else 27 return diff>0; 28 }); 29 //对凸包最后且在同一条直线上的元素按照距离从小到大进行排序 30 int r=n-1; 31 while(r>=0&&cross(trees[0],trees[n-1],trees[r])==0) 32 r--; 33 for(int l=r+1,h=n-1;l<h;l++,h--){ 34 swap(trees[l],trees[h]); 35 } 36 //用栈考察线的左拐右拐 37 stack<int>st; 38 st.push(0); 39 st.push(1); 40 for(int i=2;i<n;i++){ 41 int top=st.top(); 42 st.pop(); 43 /* 如果当前元素与栈顶的两个元素构成的向量顺时针旋转,则弹出栈顶元素 */ 44 while(!st.empty()&&cross(trees[st.top()],trees[top],trees[i])<0){ 45 top=st.top(); 46 st.pop(); 47 } 48 st.push(top); 49 st.push(i); 50 } 51 vector<vector<int> >result; 52 while(!st.empty()){ 53 result.push_back(trees[st.top()]); 54 st.pop(); 55 } 56 return result; 57 } 58 };
Andrew算法
基本思想:Andrew 使用单调链算法,该算法与 Graham扫描算分类似。它们主要的不同点在于凸壳上点的顺序。与 Graham 扫描算法按照点计较顺序排序不同,我们按照点的 x 坐标排序,如果两个点又相同的 x 坐标,那么就按照它们的 y 坐标排序。显然排序后的最大值与最小值一定在凸包上,而且因为是凸多边形,我们如果从一个点出发逆时针走,轨迹总是「左拐」的,一旦出现右拐,就说明这一段不在凸包上,因此我们可以用一个单调栈来维护上下凸壳。最大值与最小值一定位于凸包的最左边与最右边,从左向右看,我们将凸壳考虑成 2 个子边界组成:上凸壳和下凸壳。下凸壳一定是从最小值一直「左拐」直到最大值,上凸壳一定是从最大值「左拐」到最小值,因此我们首先升序枚举求出下凸壳,然后降序求出上凸壳。
具体实现:
我们首先将最初始的两个点添加到凸壳中,然后遍历排好序的 trees数组。
对于每个新的点,我们检查当前点是否在最后两个点的逆时针方向上,轨迹是否是左拐。
- 如果是的话,当前点直接被压入凸壳 hull中,cross返回的结果为正数;
- 如果不是的话,cross返回的结果为负数,我们可以知道栈顶的元素在凸壳里面而不是凸壳边上。我们继续从 hull 中弹出元素直到当前点相对于栈顶的两个点的逆时针方向上。
这个方法中,我们不需要显式地考虑共线的点,因为这些点已经按照 x 坐标排好了序。所以如果有共线的点,它们已经被隐式地按正确顺序考虑了。通过这样,我们会一直遍历到 x 坐标最大的点为止。但是凸壳还没有完全求解出来。目前求解出来的部分只包括凸壳的下半部分。现在我们需要求出凸壳的上半部分。
我们继续找下一个逆时针的点并将不在边界上的点从栈中弹出,但这次我们遍历的顺序是按照 x 坐标从大到小,我们只需要从后往前遍历有序数组 trees 即可。我们将新的上凸壳的值添加到之前的 hull数组中。最后 hull数组返回了我们需要的边界上的点。需要注意的是,由于我们需要检测上凸壳最后加入的点是否合法,此时需要再次插入最左边的点 textithull[0]进行判别。
复杂度分析:
- 时间复杂度:O(nlogn),其中 n 为数组的长度。首先需要对数组进行排序,时间复杂度为 O(nlogn),每次添加栈中添加元素后,判断新加入的元素是否在凸包上,因此每个元素都可能进行入栈与出栈一次,最多需要的时间复杂度为 O(2n),因此总的时间复杂度为 O(nlogn)
- 空间复杂度:O(n)
1 class Solution { 2 public: 3 //计算向量叉积 4 int cross(vector<int>p,vector<int>q,vector<int>r){ 5 return (q[0]-p[0])*(r[1]-q[1])-(q[1]-p[1])*(r[0]-q[0]); 6 } 7 vector<vector<int>> outerTrees(vector<vector<int>>& trees) { 8 int n=trees.size(); 9 if(n<4) 10 return trees; 11 sort(trees.begin(),trees.end(),[](const vector<int>&a,const vector<int>&b){ 12 if(a[0]==b[0]) 13 return a[1]<b[1]; 14 else 15 return a[0]<b[0]; 16 }); 17 vector<int>hull; 18 vector<bool>visited(n,false); 19 //hull[0]需要入栈两次,所以不标记 20 hull.push_back(0); 21 //求出凸包的下半部分 22 for(int i=1;i<n;i++){ 23 while(hull.size()>1&&cross(trees[hull[hull.size()-2]],trees[hull.back()],trees[i])<0){ 24 visited[hull.back()]=false; 25 hull.pop_back(); 26 } 27 visited[i]=true; 28 hull.push_back(i); 29 } 30 int m=hull.size(); 31 //求出凸包的上半部分 32 for(int i=n-2;i>=0;i--){ 33 if(!visited[i]){ 34 while(hull.size()>m&&cross(trees[hull[hull.size()-2]],trees[hull.back()],trees[i])<0){ 35 visited[hull.back()]=false; 36 hull.pop_back(); 37 } 38 visited[i]=true; 39 hull.push_back(i); 40 } 41 } 42 /* hull[0] 同时参与凸包的上半部分检测,因此需去掉重复的 hull[0] */ 43 hull.pop_back(); 44 vector<vector<int> >result; 45 for(auto v:hull) 46 result.push_back(trees[v]); 47 return result; 48 } 49 };
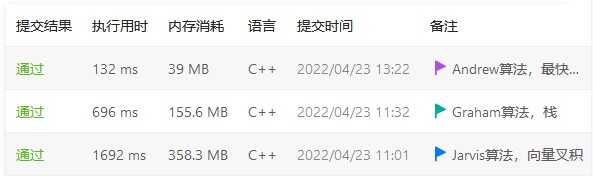
三种算法的运行效率比较




 浙公网安备 33010602011771号
浙公网安备 33010602011771号