深度学习神经网络模型原理基础

参考博客

https://www.zybuluo.com/hanbingtao/note/433855，零基础入门，讲的非常详细易懂

https://blog.csdn.net/qq_38150441/article/details/80533891，随机梯度下降

https://zhuanlan.zhihu.com/p/76772734，手推反向传播，梯度问题

西瓜书，第五章

神经网络

神经网络时机器学习的一类算法，由神经元组成。层与层之间的神经元有连接，层内之间的神经元没有连接。一个完整的神经网络有三种层：输入层、隐藏层、输出层。

感知器

感知器就是神经元。

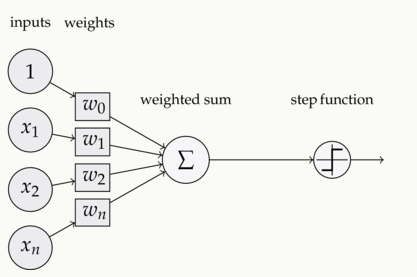
 一个神经元有如下组成部分：

• 输入权值：可以接收多个输入，每个输入对应一个权值，此外还有一个偏置项b，就是上图中的w₀
• 激活函数，根据不同的任务有不同的选择
• 输出，要传到下一个神经元

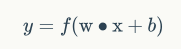
权值和偏置是神经元需要训练的参数，激活函数是固定的。

单个神经元的训练：

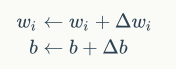
 其中：此时的激活函数是阶跃函数（大于0就是1）

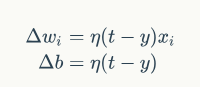
上式中，t是训练样本的实际值，也就是label。y是神经元的输出，η是学习率，控制调整参数的幅度。

编程实现见：https://www.zybuluo.com/hanbingtao/note/433855

梯度下降优化算法

为了让神经元趋向于实际值，一步一步的试出极值，参数更新需要注意激活函数、损失函数和更新的方向，以使损失函数最小。

为了向损失函数最小值的方向前进，需要向梯度的相反方向来修改参数。步幅就是学习率。

梯度是一个向量，它指向函数值上升最快的方向。显然，梯度的反方向当然就是函数值下降最快的方向了。我们每次沿着梯度相反方向去修改x的值，当然就能走到函数的最小值附近。之所以是最小值附近而不是最小值那个点，是因为我们每次移动的步长不会那么恰到好处，有可能最后一次迭代走远了越过了最小值那个点。步长的选择是门手艺，如果选择小了，那么就会迭代很多轮才能走到最小值附近；如果选择大了，那可能就会越过最小值很远，收敛不到一个好的点上。

梯度下降算法的公式：

那个倒三角是梯度算子，f(x)是损失函数，X是参数，η是学习率。

批量梯度下降算法（BGD）

针对的是整个数据集，通过对所有的样本的计算来求解梯度的方向。

优点：全局最优解；易于并行实现；

缺点：当样本数据很多时，计算量开销大，计算速度慢

小批量梯度下降算法（MBGD）

把数据分为若干个批，按批来更新参数，这样，一个批中的一组数据共同决定了本次梯度的方向，下降起来就不容易跑偏，减少了随机性

优点：减少了计算的开销量，降低了随机性

随机梯度下降算法（SGD）

在SGD算法中，每次更新w的迭代，只计算一个样本。这样对于一个具有数百万样本的训练数据，完成一次遍历就会对w更新数百万次，效率大大提升。由于样本的噪音和随机性，每次更新w并不一定按照E（损失函数）减少的方向。然而，虽然存在一定随机性，大量的更新总体上沿着E减少的方向前进的，因此最后也能收敛到最小值附近。

优点：计算速度快

缺点：收敛性能不好

 

下图展示了SGD和BGD的区别：

如上图，椭圆表示的是函数值的等高线，椭圆中心是函数的最小值点。红色是BGD的逼近曲线，而紫色是SGD的逼近曲线。我们可以看到BGD是一直向着最低点前进的，而SGD明显躁动了许多，但总体上仍然是向最低点逼近的。

反向传播算法（Back Propagation,BP）

关键在于链式求导法则。如果激活函数不同、误差计算方式不同、网络连接结构不同、优化算法不同，则具体的训练规则也会不一样。但是无论怎样，训练规则的推导方式都是一样的，应用链式求导法则进行推导即可。

首先是一个直观的三层全连接神经网络的例子：

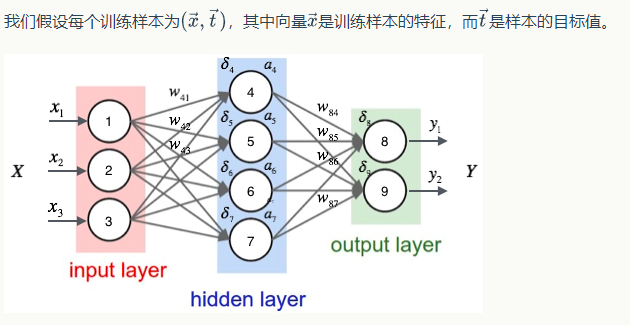
用样本的特征，计算出神经网络中每个隐藏层节点的输出，以及输出层每个节点的输出，如上图。使用的激活函数是sigmoid，损失函数是平方和损失/2.

接下来计算每个节点的误差项：

 

 

 

 

注意这里，上一层的误差随着上一层的权重传过来。前面乘上这一层的导数。

最后，更新每个连接上的权值：

 

 

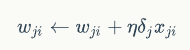
上面这个式子是由下面这个式子推导出来的。推导过程见https://www.zybuluo.com/hanbingtao/note/476663

 

 

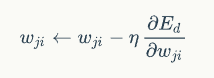
梯度消失问题

原因：多个小于1的数连乘之后，那将会越来越小，导致靠近输入层的层的权重的偏导几乎为0，也就是说几乎不更新。sigmoid可能出现，导数最大值也只能是0.25，权重初始化在01之间。梯度爆炸和梯度消失问题都是因为网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应。

解决方案：

• 改变激活函数：relu（tanh导数也小于1），但会出现dead relu
• batchnorm：批规范化，通过规范化操作将输出信号x规范化到均值为0，方差为1保证网络的稳定性。使权值w落在激活函数敏感的区域，梯度变化大，避免梯度消失，同时加快收敛。

详细解释：batchnorm就是通过对每一层的输出做scale和shift的方法，通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到接近均值为0方差为1的标准正态分布，即严重偏离的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，使得让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

• 残差结构：求导时总有1在

梯度爆炸问题

原因：大于1的数连乘下来就会导致梯度过大，导致梯度更新幅度特别大，可能会溢出，导致模型无法收敛。初始权重过大可能会导致。梯度爆炸和梯度消失问题都是因为网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应

解决方案：

• 截断，也叫做梯度剪切。其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。
• 正则化，通过对网络权重做正则限制过拟合，仔细看正则项在损失函数的形式。

 

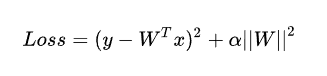
 其中，  是指正则项系数，因此，如果发生梯度爆炸，权值的范数就会变的非常大，通过正则化项，可以部分限制梯度爆炸的发生。

BP神经网络过拟合

由于其强大的表示能力，BP神经网络经常遭遇过拟合，其训练误差持续降低但测试误差可能上升。有两种策略常用来缓解BP网络的过拟合问题，第一种测量是早停（Early stopping）；第二种策略是正则化（Regularization）

全连接网络

上一层的每个节点和下一层每个节点都有连接。简称FC（Fully Connected）。只需一个包含足够多神经元的隐层，FC就能以任意精度逼近任意复杂度的连续函数。

全连接神经网络不太适合图像识别任务，主要有以下几个方面的问题：

• 参数数量太多，图像只扩大一点，参数指数级扩充。
• 没有利用像素之间的位置信息。一个神经元和上一层所有神经元相连，那么就相当于对于一个像素来说，把图像的所有像素都等同看待。学习了大量不重要的权重，学习是低效的。
• 网络层数限制。全连接神经网络的梯度很难传递超过3层。

解决这些问题的思路：

• 局部连接，只和一小部分神经元相连，减少参数。
• 权值共享，一组连接共享同一个权重。
• 下采样，使用pooling来减少每层的样本数，进一步减少参数数量，同时提高鲁棒性。

由此引出了卷积神经网络。

正则化相关

目标：为了防止过拟合

• L1、L2正则化
• Batch Normalization
• Weight Decay
• Data augmentation