1191：棋盘分割，考点：递归条件

原题：http://bailian.openjudge.cn/practice/1191/

描述

将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

 

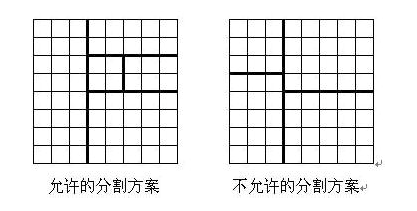
 原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的均方差最小。
均方差，其中平均值，xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n，求出O'的最小值。

输入

第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出

仅一个数，为O'（四舍五入精确到小数点后三位）。

样例输入

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

样例输出

1.633

解法

首先对均方差的公式进行分析，简化要算的内容。

 

设置递归函数func(n,x1,y1,x2,y2)表示以(x1,y1)为左上角，（x2，y2）为右下角的棋盘分割成n份后的最小平方和。从n-1份到n份有横着切、竖着切两种。

横着切：上半部分的左上角仍为(x1,y1)，右下角为(i,y2)；下半部分的左上角为(i+1,y1)，右下角为(x2,y2)。n-1份可以在上半部分，也可以在下半部分。

竖着切：左半部分的左上角仍为(x1,y1)，右下角为(x2,j)；右半部分的左上角为(x1,j+1)，右下角为(x2,y2)。n-1份可以在左半部分，也可以在右半部分。

递归边界：无法继续切的时候

 

 为了避免TLE，用一个表fval来记录中间结果。（动规）

坑：算平均值的时候用double而不是int，不然会WA

#include <iostream>
#include <cstring>
#include <iomanip>
#include <cmath>
#define INF 1<<30
using namespace std;
int chess[8][8];
int fval[15][8][8][8][8];
int func(int n, int x1, int y1, int x2, int y2) {
    if (fval[n][x1][y1][x2][y2] != -1)
        return fval[n][x1][y1][x2][y2];
    if (x2 - x1 + y2 - y1 < n - 1) {
        fval[n][x1][y1][x2][y2] = INF;
        return INF;
    }
    if (n == 1) {
        int sum = 0;
        for(int i=x1;i<=x2;i++)
            for (int j = y1; j <= y2; j++) {
                sum += chess[i][j];
            }
        fval[n][x1][y1][x2][y2] = sum * sum;
        return sum * sum;
    }
    int mmin = INF;
    for (int i = x1; i < x2; i++) {
        int temp = func(n - 1, x1, y1, i, y2) + func(1, i + 1, y1, x2, y2);
        if (temp < mmin)mmin = temp;
        temp = func(1, x1, y1, i, y2) + func(n - 1, i + 1, y1, x2, y2);
        if (temp < mmin)mmin = temp;
    }
    for (int j = y1; j < y2; j++) {
        int temp = func(n - 1, x1, y1, x2, j) + func(1, x1, j + 1, x2, y2);
        if (temp < mmin)mmin = temp;
        temp = func(1, x1, y1, x2, j) + func(n - 1, x1, j + 1, x2, y2);
        if (temp < mmin)mmin = temp;
    }
    fval[n][x1][y1][x2][y2] = mmin;
    return mmin;
}
int main()
{
    int n;
    int sum = 0;
    cin >> n;
    for (int i = 0; i < 8; i++)
        for (int j = 0; j < 8; j++)
        {
            cin >> chess[i][j];
            sum += chess[i][j];
        }
    memset(fval, -1, sizeof(fval));
    int square = func(n, 0, 0, 7, 7);
    double avg = (double)sum / n;//注意这里一定要转换成double，不然会WA
    double result = square - n * avg*avg;
    cout << fixed << setprecision(3) << sqrt(result / n) << endl;
    return 0;
}