Codeforces Round #815 (Div. 2) A-D2
https://codeforces.ml/contest/1720
A:思维 fst了。。分数,分子分母改变多少次,变一样
题意:给a / b,c / d两个分数,问分子父母各乘多少次可以得到相同的数
思路很简单,将所有数的分母变成一样,比较分子就可以了
特判:if(a == 0&& c == 0) {cout<<0<<endl;rt;} else if(a == 0 || c == 0) {cout<<1<<endl;rt;}
如果 一开始第一个数就是第二个数的约分,也只用0次。if(a * c == b * d) {cout<<0<<endl;rt;}
将所有分母变成一个数,lcm就可以,然后相应地把分子改成倍数
如果两个分子 相% = 0 ,1次就可以
//#define int ll const int N = 1e5+10; int n,m; int a,b,c,d; void solve() { // cin>>n>>m; cin>>a>>b>>c>>d; if(a == 0&& c == 0) {cout<<0<<endl;rt;} else if(a == 0 || c == 0) {cout<<1<<endl;rt;} if(a * d == b * c) { cout<<0<<endl; rt; } ll l = b / gcd(b,d) * d; a *= l / d; b *= l / d; if(a < c) swap(a,c); if(a % c == 0) { cout<<1<<endl; } else { cout<<0<<endl; } }
B:思维 最小的次大值次小值区间,不影响最大值最小值区间
题意:找一个区间[l,r],使区间内的最大值减去最小值 加上 区间外的最大值减去最小值最大
直接找出两个最大值, 两个最小值 相加再相减就可以了
为什么是对的?因为,不管数组是怎么分配的,区间可以从 某一个最大值到某一个最小值,保证区间内只有一队最大最小。
void solve() { // cin>>n>>m; cin>>n; int mx1 = 0,mx2 = 0; int mn1 = inf,mn2 = inf; fo(i,1,n) { int x;cin>>x; if(mx1 == 0 || mx1 <= x) mx2 = mx1,mx1 = x; else if(mx2 == 0 || mx2 <= x) mx2 = x; if(mn1 == inf || mn1 >= x) mn2 = mn1,mn1 = x; else if(mn2 == inf|| mn2 >= x) mn2 = x; } cout<<mx1 + mx2 - mn1 - mn2<<endl; }
C:思维 马蹄形变0,问最大修改次数
题意:每次只能马蹄形修改区间内的所有数为0,问最大修改次数
思考能不能实现每次只删除一个数
如果,一个马蹄形的空间里有两个以上的 0 ,就可以只删除一个数,实现删除次数最多,并且删除了这个1,就又多了连续的0,保证每次都只删除一个数
问题转变成了:有没有一个四边形空间,有两个以上的 0
如果有,就输出 1 的个数
如果没有,如果全是 1,那要预先删除三个 1,答案是 1的个数 -2
如果只有一个0,那预先删除 两个 1,答案是 1的个数 - 1
//-------------------------代码---------------------------- //#define int ll const int N = 600; int n,m; int a,b,c,d; char mp[N][N]; void solve() { cin>>n>>m; int num = 0; fo(i,1,n) { fo(j,1,m) { char c;cin>>c; if(c == '1') num ++ ; mp[i][j] = c; } } bool f = 0; fo(i,1,n-1){ fo(j,1,m-1) { int nn = (mp[i][j] == '1') + (mp[i+1][j+1] == '1') + (mp[i+1][j] == '1') + (mp[i][j+1] == '1'); if(nn <= 2) f = 1; } } if(f) cout<<num<<endl; else if(num == n * m) cout<<num - 2<<endl; else cout<<num-1<<endl; } void main_init() {} signed main(){ AC();clapping();TLE; cout<<fixed<<setprecision(12); main_init(); // while(cin>>n,n) // while(cin>>n>>m,n,m) int t;cin>>t;while(t -- ) solve(); // {solve(); } return 0; } /*样例区 */ //------------------------------------------------------------
D1. Xor-Subsequence (easy version) 最长上升子序列
主要是被bp,bp+1迷惑了,还以为必须是a数组里面的子序列
原来不是a数组里面的也行
可以把 bp看成 j bp+1看成 i
满足条件的时候是 bp+1 ^ a(bp) < bp ^ a(bp+1)
另外我们要知道^是怎么运算的。
a数组的值,最大只有 200,所以 a最长有 7位,对它影响最大的是 全变0或者全变 1操作,也就是±256,这个对a没什么影响,但是对b数组有影响,所以j 要从当前-256开始遍历
所以只需要枚举 i 从1到n,j 从 i - 256 到 i - 1,然后看看有没有满足条件的就可以了
也就是求最长上升子序列
dp[j] 表示 从第 1 个 到第 j 个,最长的满足条件的上升子序列长度
注意!!!! bp从0开始
//-------------------------代码---------------------------- //#define int ll const int N = 3e5+10; int n,m; int a[N]; int f[N]; void solve() { // cin>>n>>m; cin>>n; int mx = 1; f[0] = 1; fo(i,0,n-1) { cin>>a[i]; f[i] = 1; } // fo(i,1,n) cout<<f[i]<<' ';cout<<endl; for(int i = 0;i<n;i++){//bp+1 for(int j = max(0,i-256);j<i;j++) //bp if((a[j] ^ i) < (a[i] ^ (j)) ) { // dbb((a[j] ^ i),(a[i] ^ j)); f[i] = max(f[i],f[j] + 1); } mx = max(f[i],mx); } // fo(i,1,n) { // cout<<f[i]<<' '; // }cout<<endl; cout<<mx<<endl; } void main_init() {} signed main(){ AC();clapping();TLE; cout<<fixed<<setprecision(12); main_init(); // while(cin>>n,n) // while(cin>>n>>m,n,m) int t;cin>>t;while(t -- ) solve(); // {solve(); } return 0; } /*样例区 */ //------------------------------------------------------------
D2. Xor-Subsequence (hard version)
题意:找到满足 a[j] ^ i < a[i] ^ j 的最大上升子序列
小于号,要是改成等于号,左右两边同时异或 ^ i ^ j 就可以写成 a[j] ^ j = a[i] ^ i
位运算,先给 a[i] ^ i 写个trie树 :tr[p][0 / 1] 表示 编号为 p 的序列 再加一个 位置,该位置是 0/1 生成的序列的编号
要找到 比 a[i] ^ j 小的最大值,也就是 从大到小遍历 在[1,k] 位内,a[i] ^ j 和 a[j] ^ i 完全相等,这时候就用上了等于号 <=> a[i] ^ i == a[j] ^ j
第 k+1 位就会出现不相等,a[i] ^ j 在 第 k 位是1,a[j] ^ i 在第 k 位是0。当它们不相等的时候 理所当然 : 在第k位,a[i] ^ j != a[j] ^ i 。a[i] ^ j 和 a[i] ^ i 的相等关系完全等价
设 f[p][0/1] 表示 到了 trie 树的 p 编号,该位置的 i 的第k+1位 是 1或者 0时,它的最长上升子序列
状态转移:f[p][0/1] = max(maxv,f[p][0/1])
注意:当改变 某一个位置的dp值的时候,是该位置 整个trie树全部被更改成更大的值,小的值就自动被删去了。
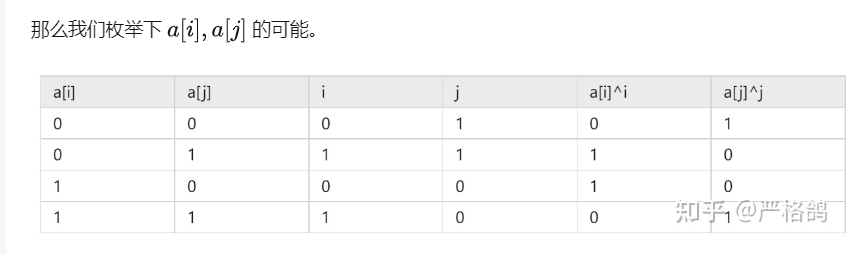
根据这张表, i 在第 k + 1 位 ,j 在第 k 位
假设 a[i] ^ i == 0 并且 i == 1 。
那就是第四种情况。如果 a[j] ^ j == 1 存在 ,即跟当前 a[i] ^ j 和 a[j] ^ i 不相等的 tr[p][1] 情况存在,同时 将 最大上升子序列 更新成 a[j] ^ j == 1 且 j == 0 的最大值 :mx = max( f[tr[p][1]][0] , mx);
//-------------------------代码---------------------------- #define int ll const int N = 3e5+10; int tr[N * 40][2]; int f[N * 40][2]; int n,m,a[N],idx; //构建 a[i] ^ i trie树 void insert(int x,int y) { int p = 0; of(i,30,0) { int u = x >> i & 1,v = y >> i & 1; if(u == v) { if(!tr[p][0]) tr[p][0] = ++ idx; p = tr[p][0]; } else { if(!tr[p][1]) tr[p][1] = ++ idx; p = tr[p][1]; } } } int query(int x,int y) { int p = 0,maxv = 0; of(i,30,0) { int u = x >>i & 1,v = y >> i & 1; if(u != v) { if(tr[p][0]) { if(u == 1) maxv = max(maxv,f[tr[p][0]][1]); else maxv = max(maxv,f[tr[p][0]][0]); } if(!tr[p][1]) break; p = tr[p][1]; } else { if(tr[p][1]) { if(u == 1) maxv = max(maxv,f[tr[p][1]][0]); else maxv = max(maxv,f[tr[p][1]][1]); } if(!tr[p][0]) break; p = tr[p][0]; } } return maxv + 1; } //更新 i ^ a[i] 每一位的最长上升子序列 ,并标记 i 在这一位的值 void dp(int x,int y,int maxv) { int p = 0; of(i,30,0) { int u = x >> i & 1,v = y >> i & 1; if(u == v) p = tr[p][0]; else p = tr[p][1]; if(u == 1) f[p][1] = max(f[p][1],maxv); else f[p][0] = max(f[p][0],maxv); } } void solve() { // cin>>n>>m; cin>>n; int res = 0; fo(i,0,n-1) { cin>>a[i]; int maxv = query(i,a[i]); res = max(res,maxv); insert(i,a[i]); dp(i,a[i],maxv); } cout<<res<<endl; fo(i,0,idx) { tr[i][0] = tr[i][1] = 0; f[i][0] = f[i][1] = 0; } idx = 0; } void main_init() {} signed main(){ AC();clapping();TLE; cout<<fixed<<setprecision(12); main_init(); // while(cin>>n,n) // while(cin>>n>>m,n,m) int t;cin>>t;while(t -- ) solve(); // {solve(); } return 0; } /*样例区 */ //------------------------------------------------------------



 浙公网安备 33010602011771号
浙公网安备 33010602011771号