洛谷 P6242 【模板】线段树 3 吉司机线段树 区间取最小值 维护历史最大值和区间和
题目背景
本题是线段树维护区间最值操作与区间历史最值的模板。
题目描述
给出一个长度为 nn 的数列 AA,同时定义一个辅助数组 BB,BB 开始与 AA 完全相同。接下来进行了 mm 次操作,操作有五种类型,按以下格式给出:
1 l r k:对于所有的 i\in[l,r]i∈[l,r],将 A_iAi 加上 kk(kk 可以为负数)。2 l r v:对于所有的 i\in[l,r]i∈[l,r],将 A_iAi 变成 \min(A_i,v)min(Ai,v)。3 l r:求 \sum_{i=l}^{r}A_i∑i=lrAi。4 l r:对于所有的 i\in[l,r]i∈[l,r],求 A_iAi 的最大值。5 l r:对于所有的 i\in[l,r]i∈[l,r],求 B_iBi 的最大值。
在每一次操作后,我们都进行一次更新,让 B_i\gets\max(B_i,A_i)Bi←max(Bi,Ai)。
输入格式
第一行包含两个正整数 n,mn,m,分别表示数列 AA 的长度和操作次数。
第二行包含 nn 个整数 A_1,A_2,\cdots,A_nA1,A2,⋯,An,表示数列 AA。
接下来 mm 行,每行行首有一个整数 opop,表示操作类型;接下来两个或三个整数表示操作参数,格式见【题目描述】。
输出格式
对于 op\in\{3,4,5\}op∈{3,4,5} 的操作,输出一行包含一个整数,表示这个询问的答案。
输入输出样例
5 6 1 2 3 4 5 3 2 5 1 1 3 3 4 2 4 2 3 4 1 5 1 5 3 1 4
14 6 6 11
说明/提示
样例说明 #1
| 操作次数 | 输入内容 | 操作 | 数列 | 输出结果 |
|---|---|---|---|---|
| 0 | 1,2,3,4,51,2,3,4,5 | |||
| 1 | 3 2 5 |
求出 [2,5][2,5] 所有数的和 | 1,2,3,4,51,2,3,4,5 | 14 |
| 2 | 1 1 3 3 |
将 [1,3][1,3] 内所有数加 33 | 4,5,6,4,54,5,6,4,5 | |
| 3 | 4 2 4 |
求出 [2,4][2,4] 所有数的最大值 | 4,5,6,4,54,5,6,4,5 | 6 |
| 4 | 2 3 4 1 |
将 [3,4][3,4] 所有数与 11 取最小值 | 4,5,1,1,54,5,1,1,5 | |
| 5 | 5 1 5 |
求出 [1,5][1,5] 所有位置历史最大值的最大值 | 4,5,1,1,54,5,1,1,5 | 6 |
| 6 | 3 1 4 |
求出 [1,4][1,4] 所有数的和 | 4,5,1,1,54,5,1,1,5 | 11 |
数据规模与约定
- 对于测试点 1,21,2,满足 n,m\leq 5000n,m≤5000;
- 对于测试点 3,43,4,满足 op\in\{1,2,3,4\}op∈{1,2,3,4};
- 对于测试点 5,65,6,满足 op\in\{1,3,4,5\}op∈{1,3,4,5};
- 对于全部测试数据,保证 1\leq n,m\leq 5\times 10^51≤n,m≤5×105,-5\times10^8\leq A_i\leq 5\times10^8−5×108≤Ai≤5×108,op\in[1,5]op∈[1,5],1 \leq l\leq r \leq n1≤l≤r≤n,-2000\leq k\leq 2000−2000≤k≤2000,-5\times10^8\leq v\leq 5\times10^8−5×108≤v≤5×108。
提示
本题输入量较大,请使用合理高效的读入方法。
分析
https://www.luogu.com.cn/problem/solution/P6242
mx:最大值。mx_:历史最大值。se:次大值。cnt:最大值个数。sum:区间和。add1:加法懒标记。add1_:历史最大加。add2:次大值加法懒标记。add2_:次大值历史最大加。
条件1:维护区间和,并且维护加法懒标记即可实现区间加法
条件2:使区间每个值变成min(当前值,v)。懒标记比较难实现精准的单点取最小值,但是如果仅是查询区间求和,可以通过维护最大值,次大值,最大值的个数,区间和,加法懒标记这几个元素来实现
首先对于区间取最小值,有三种情况:
1. 当前最大值 比 v 小。不用修改任何值
2. 当前区间次大值 比 v 小,最大值比v 大,sum += cnt * (最大值 - v)
3. 次大值比v 大,无法直接得到sum,需要往下传递,进行修改,然后push_up上去,直接修改当前的sum为左右子树的加和
为什么不能直接维护单个最大值,然后直接找到满足条件的位置并且传递上去呢?
这样要遍历到叶子节点,维护最大值和次大值减小时间复杂度。
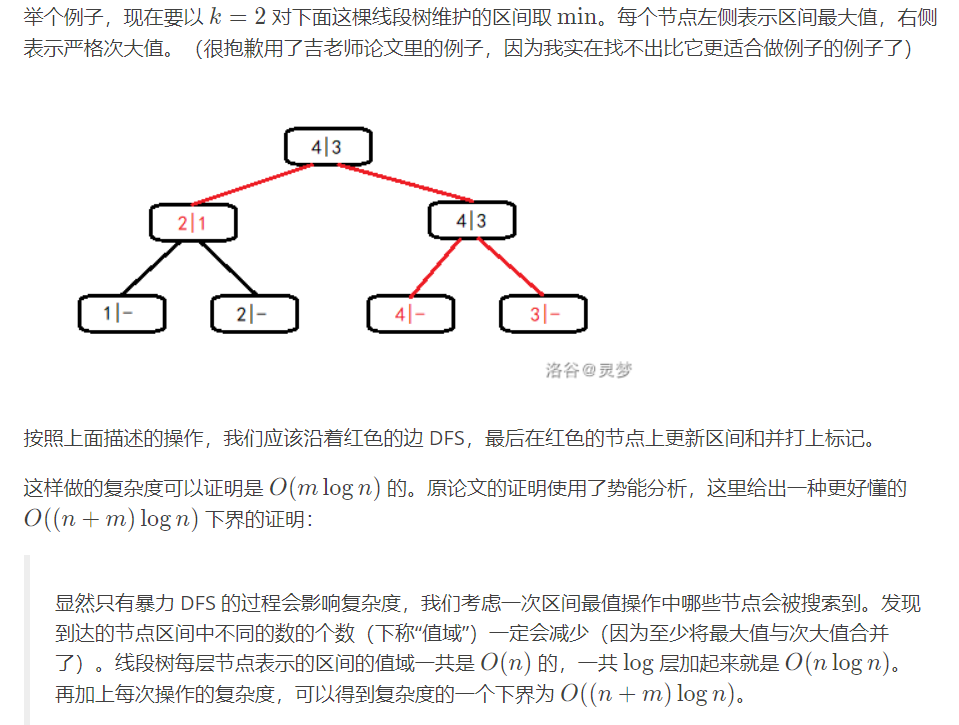
不是很懂。但是nlogn可以理解,查询复杂度变成nlogn了。

感觉意思就是,当前代码既有历史最大值,也有最大值,还维护了一堆值,就说它是logn了。最终复杂度也变成了mlog^2
条件3:区间求和,维护sum。
条件4:区间求最大值,维护mx
条件5:区间求历史最大值
维护mx_历史最大值,add1_最大值的历史最大加法懒标记,add2_次大值的历史最大加法懒标记。
push_down操作时,设当前节点为u ,子节点为v。
v.add1_ = max(v.add1_,v.add1 + u.add1_)
v.mx_ = max(v.mx_,v.mx + u.add1_)
//-------------------------代码---------------------------- #define int ll const int N = 5e5+10; int n,m; struct node { int l,r; int mx,mx_,se,cnt;ll sum; int add1,add1_,add2,add2_; }tr[N<<2]; int a[N]; #define root tr[u] #define lt tr[ul] #define rh tr[ur] void push_up(int u) { if(root.l == root.r) rt; tr[u].sum = lt.sum + rh.sum; root.mx_ = max(tr[ul].mx_,rh.mx_); if(lt.mx == rh.mx) { root.mx = lt.mx; root.se = max(rh.se,lt.se); root.cnt = rh.cnt + lt.cnt; } else if(lt.mx > rh.mx) { root.mx = lt.mx; root.se = max(rh.mx,lt.se); root.cnt = lt.cnt; } else if(rh.mx > lt.mx) { root.mx = rh.mx; root.se = max(rh.se,lt.mx); root.cnt = rh.cnt; } } void upt(int u,int k1,int k1_,int k2,int k2_) { //区间和更新,最大值更新了多少,除了最大值之外的值更新了多少 root.sum += 1ll * k1 * root.cnt + 1ll * k2 * (root.r - root.l + 1 - root.cnt); root.mx_ = max(root.mx_,root.mx + k1_);//历史最大值更新 root.add1_ = max(root.add1_,root.add1 + k1_);//历史最大增加值更新 root.mx += k1,root.add1 += k1;//最大值增加k1// root.add2_ = max(root.add2_,root.add2 + k2_);//厉害次大增加值更新 if(root.se != -INF) root.se += k2;//次大值如果有的话更新 root.add2 += k2;//次大增加值更新 } void push_down(int u) { int tmp = max(lt.mx,rh.mx); if(lt.mx == tmp) { upt(ul,root.add1,root.add1_,root.add2,root.add2_); } else upt(ul,root.add2,root.add2_,root.add2,root.add2_); if(rh.mx == tmp) { upt(ur,root.add1,root.add1_,root.add2,root.add2_); } else upt(ur,root.add2,root.add2_,root.add2,root.add2_); root.add1 = root.add1_ = root.add2 = root.add2_ = 0; } void build(int u,int l,int r) { tr[u].l=l, tr[u].r=r; tr[u].add1=tr[u].add1_=tr[u].add2=tr[u].add2_=0; if(l == r) { root.sum = tr[u].mx_ = tr[u].mx = a[l]; tr[u].se = -INF,tr[u].cnt = 1;rt; } build(ul,l,tr_mid);build(ur,tr_mid+1,r); push_up(u); } void modify1(int u,int l,int r,int k) { if(l <= tr[u].l && tr[u].r <= r) { upt(u,k,k,k,k);rt; } if(r < tr[u].l || l > tr[u].r) rt; push_down(u); modify1(ul,l,r,k);modify1(ur,l,r,k); push_up(u); } void modify2(int u,int l,int r,int k) { if(root.l > r || root.r < l || k >= root.mx) rt; if(l <= root.l && root.r <= r && k > root.se) { upt(u,k-root.mx,k-root.mx,0,0);rt; } push_down(u); modify2(ul,l,r,k);modify2(ur,l,r,k); push_up(u); } ll query3(int u,int l,int r) { if(l > root.r || r < root.l) return 0; if(tr[u].l >= l && root.r <= r) return root.sum; push_down(u); return query3(ul,l,r) + query3(ur,l,r); } ll query4(int u,int l,int r) { if(l > root.r || r < root.l) return -INF; if(tr[u].l >= l && root.r <= r) return root.mx; push_down(u); return max(query4(ul,l,r) , query4(ur,l,r)); } ll query5(int u,int l,int r) { if(l > root.r || r < root.l) return -INF; if(tr[u].l >= l && root.r <= r) return root.mx_; push_down(u); return max(query5(ul,l,r) , query5(ur,l,r)); } void solve() { read(n);read(m); fo(i,1,n) read(a[i]); build(1,1,n); while(m--) { int op,l,r,k;read(op); if(op == 1) { read(l);read(r);read(k); modify1(1,l,r,k);; } if(op == 2) { read(l);read(r);read(k); modify2(1,l,r,k); } if(op == 3) { read(l);read(r); cout<<query3(1,l,r);cout<<endl; } if(op == 4) { read(l);read(r); cout<<query4(1,l,r);cout<<endl; } if(op == 5) { read(l);read(r); cout<<query5(1,l,r)<<endl;; } } } void main_init() {} signed main(){ AC();clapping();TLE; cout<<fixed<<setprecision(12); main_init(); // while(cin>>n,n) // while(cin>>n>>m,n,m) // int t;cin>>t;while(t -- ) solve(); // {solve(); } return 0; } /*样例区 */ //------------------------------------------------------------


 浙公网安备 33010602011771号
浙公网安备 33010602011771号