1014 Accumulation Degree 换根DP变式

 链接：https://ac.nowcoder.com/acm/problem/51180
来源：牛客网

题目描述

Trees are an important component of the natural landscape because of their prevention of erosion and the provision of a specific ather-sheltered ecosystem in and under their foliage. Trees have also been found to play an important role in producing oxygen and reducing carbon dioxide in the atmosphere, as well as moderating ground temperatures. They are also significant elements in landscaping and agriculture, both for their aesthetic appeal and their orchard crops (such as apples). Wood from trees is a common building material.

Trees also play an intimate role in many of the world's mythologies. Many scholars are interested in finding peculiar properties about trees, such as the center of a tree, tree counting, tree coloring. A(x) is one of such properties.

A(x) (accumulation degree of node x) is defined as follows:

1. Each edge of the tree has an positive capacity.
2. The nodes with degree of one in the tree are named terminals.
3. The flow of each edge can't exceed its capacity.
4. A(x) is the maximal flow that node x can flow to other terminal nodes.

Since it may be hard to understand the definition, an example is showed below:

A(1)=11+5+8=24
Details:	1->2	11
	1->4->3	5
	1->4->5	8(since 1->4 has capacity of 13)
A(2)=5+6=11
Details:	2->1->4->3	5
	2->1->4->5	6
A(3)=5
Details:	3->4->5	5
A(4)=11+5+10=26
Details:	4->1->2	11
	4->3	5
	4->5	10
A(5)=10
Details:	5->4->1->2	10

The accumulation degree of a tree is the maximal accumulation degree among its nodes. Here your task is to find the accumulation degree of the given trees.

输入描述:

The first line of the input is an integer T which indicates the number of test cases. The first line of each test case is a positive integer n. Each of the following n - 1 lines contains three integers x, y, z separated by spaces, representing there is an edge between node x and node y, and the capacity of the edge is z. Nodes are numbered from 1 to n.
All the elements are nonnegative integers no more than 200000. You may assume that the test data are all tree metrics.

输出描述:

For each test case, output the result on a single line.

示例1

输入

复制 1 5 1 2 11 1 4 13 3 4 5 4 5 10

1
5
1 2 11
1 4 13
3 4 5
4 5 10

输出

复制 26

26

分析

流量：1->4 时权值为13 ，1->4->5权值为10可以把13分配10给它，1->4->3权值为5，目前只剩下13-10=3的流量所以只能分配3点流量给它。

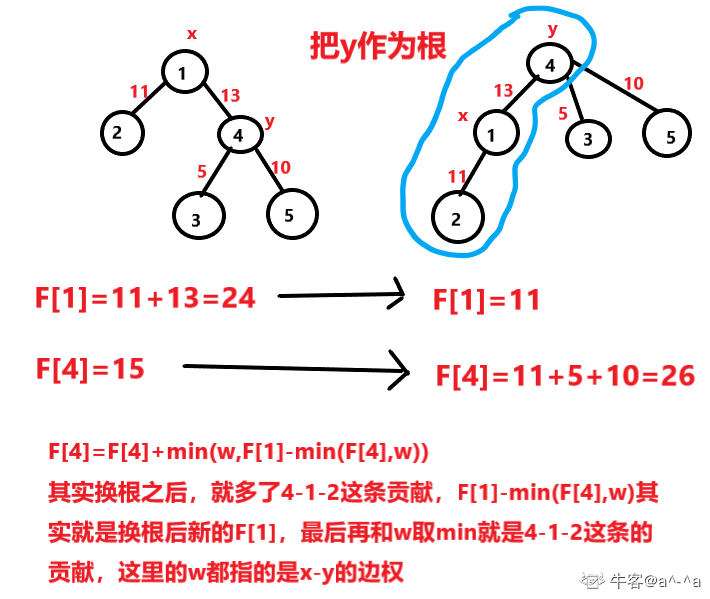
设f[v] 为当前节点能够向下传递的最大流量。 f[1] 就是13。f[4] 就是10 + 5 = 15（它的叶子节点没有流量限制）。可以看出f[1] = min(w ，f[4])；

这题题意就是选择那个根，能够使向下流的流量最大化。所以肯定是换根DP

先跑一边dfs，算出每个节点的流量。如果是叶子节点，流量f = 0。如果子节点是叶子节点，f += f[son]。如果子节点不是叶子节点，f += min(f[son],w)

然后考虑换根，如果换叶子节点为根，f[son] += w，

 

 

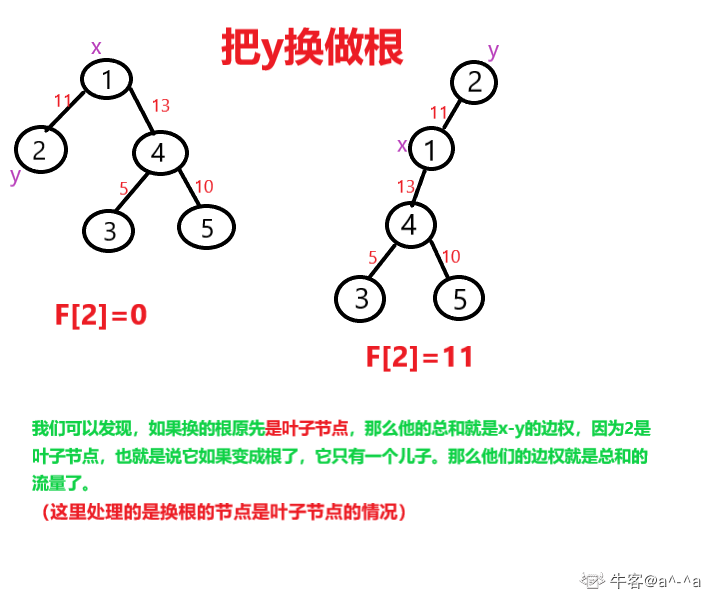
如果换普通的节点为根，f[son] = min(w,f[u] - min(w,f[son]))

 

 

 

//-------------------------代码----------------------------

#define int ll
const int N = 400010;
int e[N],f[N],w[N],ne[N],h[N],idx;
int n,m,d[N],g[N];

void add(int a,int b,int c) {
    e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx ++ ;
}

void dfs1(int u,int fa) {
    for(int i = h[u];~i;i=ne[i]) {
        int son = e[i];
        if(son == fa) continue;
        dfs1(son,u);
        if(d[son] == 1) f[u] += w[i];
        else f[u] += min(w[i],f[son]);
    }
}

void dfs2(int u,int fa) {
    for(int i=h[u];~i;i=ne[i]){
        int v=e[i];
        if(v==fa)continue;
        if(d[u]==1) g[v]=f[v]+w[i];
        else g[v]=f[v]+min(g[u]-min(f[v],w[i]),w[i]);
        dfs2(v,u);
    }
}

void solve()
{
//    cin>>n>>m;
    ms(f,0);
    ms(h,-1);
    ms(d,0);
    idx = 0;
    cin>>n;
    fo(i,1,n-1) {
        int x,y,z;cin>>x>>y>>z;
        add(x,y,z);d[x]++;
        add(y,x,z);d[y]++;
    }
    dfs1(1,0);
    g[1]=f[1];
    dfs2(1,0);
    int ans=-1;
    for(int i=1;i<=n;i++)ans=max(ans,g[i]);
    cout<<ans<<endl;
}

signed main(){
    AC();
    clapping();TLE;

    int t;cin>>t;while(t -- )
    solve();
//    {solve(); }
    return 0;
}

/*样例区


*/

//------------------------------------------------------------