1011 同余方程 扩展欧几里得定理 求逆元总结

链接：https://ac.nowcoder.com/acm/contest/26656/1011
来源：牛客网

题目描述

求关于x的同余方程ax≡1(modb)ax \equiv1 \pmod{b}ax≡1(modb)的最小正整数解。

输入描述:

输入只有一行，包含两个正整数a,b，用一个空格隔开。

输出描述:

输出只有一行，包含一个正整数x0x_0x0​，即最小正整数解。输入数据保证一定有解。

示例1

输入

复制 3 10

3 10

输出

复制 7

7

备注:

对于40%的数据，有2≤b≤1 0002 \leq b \leq 1 \,0002≤b≤1000；
对于60%的数据，有2≤b≤50 000 0002 \leq b \leq 50 \,000 \,0002≤b≤50000000；
对于100%的数据，有2≤a,b≤2 000 000 0002 \leq a,b \leq 2 \,000 \,000 \,0002≤a,b≤2000000000。

分析

1.b是质数：费马小定理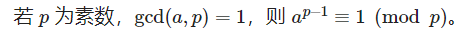    

逆元就是 a^(p-2)

2.a，b互质：欧拉定理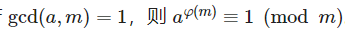     

逆元就是 a^(φ(m)-1)

3.a，b不互质：线性同余方程（二元一次方程）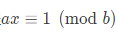 

 

逆元直接套公式代出来

 

这题就是第三种情况

只不过最后如果x 小于0，让它变成最小的情况，就要让它的增量和 b 的减量抵消，那a  * x 的最小增量就是最小公倍数，

x = lcm(a,b) / a = a * b / gcd(a,b) / a = b / gcd(a,b)

然后题解是 x = (x % b + b) % b  

证明：（题解只不过把t 变成了b ）

 

 

#include<bits/stdc++.h>
using namespace std;


// ax + by = 1
// ax + b(y + k) = 1
#define int long long
int gcd_ex(int a,int b,int &x,int &y) {
    if(b == 0) {x = 1,y = 0;return a;}
    int d = gcd_ex(b,a%b,y,x);
    y = y - (a / b) * x;
    return d;
}

signed main() {
    
    int a,b;cin>>a>>b;
    int x,y;
    gcd_ex(a,b,x,y);
    if(x<0)x += b / __gcd(a,b);
    cout<<x<<endl;
}