未来的公式挖掘机？大数据的秘密-符号回归(Symbolic Regressor)-1

符号回归(Symbolic Regressor)

符号回归简介

符号回归是一种机器学习技术，旨在识别一个潜在的数学表达式。它首先建立一个朴素随机公式的总体来表示已知自变量和它们的因变量目标之间的关系，以预测新数据。每一个连续的生成程序从之前的程序进化而来，从种群中选择最适合的个体进行遗传操作。符号回归依托于达尔文的自然选择理论，利用计算机程序间模拟基因复制、交叉和突变等操作，在初始群体较大且交叉、变异概率设置合理的情况下，不会陷入局部最优解，可以基于大量实际数据寻找隐藏在随机数值后的规律，相较于传统回归方法，所得到的拟合函数具有更广泛的适用性和更高的精确度。遗传编程是符号回归的核心算法，通过引入自定义函数以及动态程序服务方法，在机器学习、人工智能、组合优化、自适应系统以及控制技术等领域中的应用都取得了显著的效果。

Genetic Programming（GP）简介

解决符号回归（SR） 问题最常用的算法是 Genetic Programming（GP）。
遗传编程是符号回归的核心算法，通过引入自定义函数以及动态程序服务方法，在机器学习、人工智能、组合优化、自适应系统以及控制技术等领域中的应用都取得了显著的效果。
相较于遗传算法采用固定长度字符串编码的方式，遗传编程则通过使用函数表达式的方法克服无法描述层次化的问题及缺少动态可变性等缺陷。
遗传编程以函数本身特点为基础，采用二叉树（Binary Tree）结构，将函数表达式用于数据结构中，进而把遗传算法中针对二进制为串的遗传操作改进形成针对二叉树的遗传操作。

GP符号回归常用库之Gplearn

Gplearn扩展了scikit学习机器学习库，通过符号回归执行遗传编程(GP)。
相较于遗传算法采用固定长度字符串编码的方式，遗传编程则通过使用函数表达式的方法克服无法描述层次化的问题及缺少动态可变性等缺陷。遗传编程以函数本身特点为基础，采用二叉树（Binary Tree）结构，将函数表达式用于数据结构中，进而把遗传算法中针对二进制为串的遗传操作改进形成针对二叉树的遗传操作。
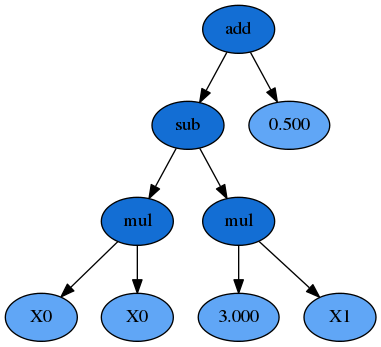
基因编程能够采取一系列完全随机的程序，（未经训练，你可能也想不到的任何给定的目标功能），并使它们繁殖，变异和进化它们的方式走向真相。我们可以把遗传规划看作是一个随机优化的过程。每一个初始种群被构思出来，在这个过程中的每一个选择和进化步骤中，从当前一代的随机个体被选择来经历随机变化以进入下一代。您可以通过使用估计器（estimator）的random_state参数来控制这种随机性。在每一种表示中，我们都有变量、常数和函数的混合。在这种情况下，我们有加、减、乘的函数。我们也有变量𝑋0和𝑋1，常数是3.0和0.5。总的来说，这些变量和常数被称为终端。与函数相结合，可用变量、常量和函数的集合被称为原语集。
我们也可以将这个公式表示为一个语法树，其中函数是内部节点，用深蓝色表示，变量和常量组成了叶子（或终端节点）用浅蓝色表示：

在gplearn中，可用的函数集由一个在初始化估计器时设置的参数控制。默认集是算术运算符：加法、减法、除法和乘法。但是，您也可以添加一些所有内置的转换器、比较函数或三角函数。这些字符串被放到function_set参数中，以便将它们包含在程序中。

符号转换器是一种有监督的转换器，它首先构建一组简单的随机公式来表示一种关系。这些公式用树状结构表示，数学函数递归地应用于变量和常数。每一代程序都是从前一代进化而来，通过从群体中选择最适合的个体进行遗传操作，如交叉、突变或繁殖。最终的种群是寻找最适合的个体，彼此之间的相关性最小。

常用基本函数
• ‘add’ : addition, arity=2.
• ‘sub’ : subtraction, arity=2.
• ‘mul’ : multiplication, arity=2
• ‘div’ : division, arity=2.
• ‘sqrt’ : square root, arity=1.
• ‘log’ : log, arity=1.
• ‘abs’ : absolute value, arity=1.
• ‘neg’ : negative, arity=1.
• ‘inv’ : inverse, arity=1.
• ‘max’ : maximum, arity=2.
• ‘min’ : minimum, arity=2.
• ‘sin’ : sine (radians), arity=1.
• ‘cos’ : cosine (radians), arity=1.
• ‘tan’ : tangent (radians), arity=1.

总结

符号回归是一种估计器，它首先建立一组简单的随机公式来表示一种关系。这些公式用树状结构表示，数学函数递归地应用于变量和常数。每一代程序都是从前一代进化而来，通过从群体中选择最适合的个体进行遗传操作，如交叉、突变或繁殖。
符号回归是一种机器学习技术，它通过基本函数可以自动发现数学表达式来拟合给定的数据集。与传统的回归技术不同，符号回归不仅可以找到一个数学模型来拟合数据，还可以生成一个解析式，从而提供更深入的理解。符号回归的核心思想是使用遗传算法或其他优化技术来搜索数学表达式空间，以找到与训练数据最匹配的表达式。这些表达式可以是任何形式的数学公式，包括加减乘除、三角函数、对数函数等。这些表达式在不同的数据集上可以有不同的形式。符号回归可以用于多种应用，如函数逼近、系统辨识、特征选择、时间序列预测等。在某些领域，符号回归已经被证明比传统的回归技术更有效。然而，符号回归的计算复杂度往往比传统的回归技术更高，因为它需要搜索更广的表达式空间。因此，在实际应用中，需要权衡精度和计算资源之间的折衷。