微分方程概述
微分方程简介：
- 包含连续变化的自变量、未知函数及其导数的 方程
- 常微分方程、偏微分方程
- 微分方程的阶
- 微分方程的解、通解、特解、初始条件，解析 解、数值解
微分方程模型：
什么时候需要建立微分方程模型？
- 研究对象涉及某个运动过程 或物体随时间连续变化的规律
- 可归结为研究函数变化规律的问题
- 工程、经济管理、人口、环境、生态、交通等 众多领域有广泛应用
怎样建立微分方程模型？
- 机理分析方法 如研究对象为数学、物理等领域的问题，利 用该领域定律、规律 对其它领域（如经济、医药等）问题，具体 分析领域机理，找出规律
- 微元法：寻找一些微元之间的关系式，经常 需要对微元应用已知定律、规律
- 模拟近似法
犯罪嫌疑人问题：
某公安局于晚上19:30发现一具尸体，当 天20:20，法医测得尸体温度为32.6℃， 一个小时后又测得尸体温度为31.4 ℃。假 定在这几个小时内室温一直为21.1 ℃。根 据案情线索警方确定张某为主要嫌疑人， 但张某矢口否认，并有证人称：“下午张 某一直在办公室，下午5点打了一个电话 后才离开。”从办公室到案发现场步行需 要5分钟。能否排除张某的嫌疑？
分析：
- 排除张某作案嫌疑的主要依据 是看张某是否有作案时间，这需要知道被害人死亡的时间
- 所以需要根据现在已有的线索，推测出被害人的死亡时间
- 尸体温度随时间变化符合牛顿冷却定律，据此可以建立微分方程模型
假设：
-
被害人遇害前体温为37 ℃
-
符号说明：
T(t)表示t时刻尸体的温度
k表示散热系数
T0=21.1 ℃表示环境温度
t=0表示晚上20:20这一刻，所以 T(0)= 32.6 ，T(1)=31.4
\[\frac{dT}{dt}=k(T-T_0)
\]
这是一个可分离变量的一阶线性微分方程
\[解为:T(t)=T_0+C_e{^{kt}}
\]
把T（0）=32.6，T（1）=31.4代入T（t）可得：
\[\begin{cases}
T(0)=21.1+c=32.6\\
T(1)=21.1+C_e{^k}=31.4
\end{cases}\\
\Downarrow
\\C=11.5,k=-0.1102\\
令21.1+11.5_{e^{-0.1102t}}=37\\
\Downarrow\\
t=-2.9399
\]
2.9399小时约为2小时56分，可知被害人遇害 时间大约为：下午8点20分-2小时56分=下午5 点24分 • 可见张某不能摆脱嫌疑！
容器漏水问题：
有一个半球形容器，高为1m，水从其底部 的小孔流出。小孔横截面积为1cm2 。开始时 容器内盛满水，分析水从小孔流出过程中容 器中水面高度h(水面与孔口中心的距离)随时 间t如何变化。
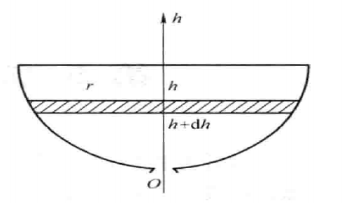
分析：
由流体力学可知，通过孔口横截面的水的体积V 对时间t的变化率可由以下公式计算
\[\frac{dV}{dt}=0.62S\sqrt{2gh}
\]
其中0.62为流量系数，S为孔口横截面积，此处 S=1cm2 。
而由微元法，设在时间间隔[t, t+dt]内，水面高度由h下降到h+dh（dh<0），可得
\[dV=-\pi r^2dh\\
又\quad r=\sqrt{100^2-(100-h)^2}=\sqrt{200h-h^2}
\]
所以：
\[dV=-\pi(200h-h^2)dh
\]
结合流体力学公式和微元法，可得：
\[0.62S\sqrt{2gh}dt=-\pi (200h-h^2)dh\\
初始条件为：h|_{t=0}=100
\]
解此方程，得到水面高度h与时间t的关系
\[t=\frac{\pi}{4.65\sqrt{2g}}(7\times10^5-10^3h^{\frac{3}{2}}+3h^{\frac{3}{2}})
\]
