整数线性规划

现在有一个厂家打算用集装箱托运甲乙两种货物，每箱的体积、重量、可 获利润以及托运所受限制如下表所示：

其中，货物甲每箱 5 立方米，重 200 斤，托运一箱可获利 2 千元，也就是 20 个百元；

货物乙每箱 4 立方米，重 500 斤，托运一箱可获利 1 千元，也就是 10 个百元；

由于集装箱的大小及承载量有限，只能托运不大于 24 立方米且重量不超过 13 个百斤的货物。

问两种货物各托运多少箱，可使获得利润为最大？

显然这是一个最优化问题，目的是获取最大利润。决策变量是托运甲、乙 两种货物的箱数，为此，我们设甲乙两种货物分别托运x1箱和x2箱，于是目标就 是求𝑥1和𝑥2，使得20x1 + 10x2最大。

注意到托运限制体积是 24 立方米，因此5x1 + 4x2 ≤ 24；

托运限制重量是 13，所以2x1 + 5x2 ≤ 13

此外，我们还需要注意到托运的箱数必须非负；不仅如此，由于本题托运货 物按箱计算，所以x1和x2还必须为整数。

因此本题的数学模型是：目标函数20𝑥1 + 10𝑥2取最大值，并且它受到 4 个约 束条件的限制

\[max\quad z=20x_1+10x_2\\ s.t. \begin{cases} 5x_1+4x_2\le 24\\ 2x_1+5x_2\le 13\\ x_1,x_2\ge 0,x_1,x_2\in Z \end{cases} \]

这个模型和的线性规划非常像，唯一的区别是增加了对自变量是 整数的限制，这类规划问题属于整数规划。

决策变量（全部或部分）限制为整数的规划称为整数规划。整数规划的英文 翻译是 integer program, 简称 IP。

若在线性模型中，变量限制为整数，则称为整数线性规划，即 ILP。目前所 流行的求解整数规划的方法往往只适用于整数线性规划。

整数规划又分以下四类：

1. 纯整数规划：所有决策变量均要求为整数
2. 混合整数规划：部分决策变量要求为整数
3. 纯 0－1 规划：所有决策变量均要求为 0 或者 1
4. 混合 0－1 规划：部分决策变量要求为 0 或者 1

整数规划与线性规划不同这处在于增加了整数约束。如果不考虑整数约束， 那么对应的线性规划称为整数规划的线性松弛模型。

Matlab 在求解整数规划时，调用函数 intlinprog (), 其具体格式为:

[x,favl]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)

该函数的使用和 linprog 函数的使用十分相似，区别在于，intlinprog ()函数在 linprog 函数的基础上多了一个参数——intcon。

intcon 的意义为整数约束变量的位置，这个位置是按照目标函数和约束条件 中变量位置来排列的。

以引例来说，它的数学模型是:

\[max\quad z=20x_1+10x_2\\ s.t. \begin{cases} 5x_1+4x_2\le 24\\ 2x_1+5x_2\le 13\\ x_1,x_2\ge 0,x_1,x_2\in Z \end{cases} \]

M文档如下：

c=[-20,-10];
intcon=[1,2];
A=[5,4;2,5];
b=[24;13];
vlb=zeros(2,1);
[x,fval]=intlinprog(c,intcon,A,b,[],[],vlb,[])

在程序的第二行中，语句 intcon=[1,2]表明𝑥1和𝑥2都为整数。

得到结果如下：

x =
 3.9205
 0.2291
 26.0000
fval =
 2.0584

也就是托运 4 箱 A 货物和 1 箱 B 货物，可以获得最大利润，最大利润为 90 个百 元单位，即 9000 元。

接下来我们通过一个例子来看看混合整数规划问题的求法。

超市里有 3 种食品，玉米，牛奶和面包，单价，所含的维他命 A 和卡路里 的信息如下。

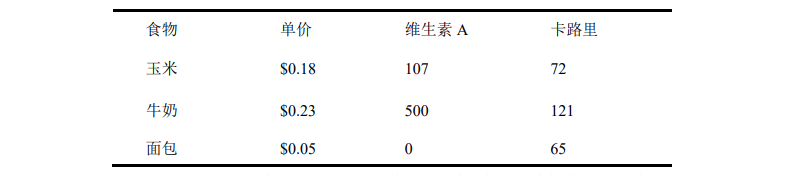
问题是买多少份的玉米，牛奶，面包，使得总价格最低，而维他命 A 的总摄取 量不小于 500 但不大于 50000，卡路里的总摄取量不小于 2000 但不大于 2250， 面包的份数必须是整数。

模型如下：

\[min \quad z=0.18x_1+0.23x_2+0.05x_3\\ s.t.\begin{cases} 500\le 107x_1+500x_2\le 50000\\ 2000\le 72 x_1+121x_2+65x_3\le 2250\\ x_1,x_2,x_3\ge 0,x_1\in Z \end{cases} \]

编程如下：

c=[0.18,0.23,0.05];
intcon=3; % intcon=3 代表𝑥3是整数。
A=[107,500,0;72,1212,65;
 -107,-500,0;-72,-121,-65];
b=[5000;2250;-500;-2000];
vlb=zeros(3,1);
[x,fval]=intlinprog(c,intcon,A,b,[],[],vlb,[])

结果如下：

x =
 3.9205
 0.2291
 26.0000
 
 
fval =
 2.0584