【笔记篇】最良心的计算几何学习笔记(五)
如果有一天拥抱的温度可以找到它永远的主人。 如果有一天白色的云与蓝色的苍穹颠倒了颜色。 如果有一天紫罗兰在盛放之前就呈现出它最美的花瓣。 如果有一天世界上没有了风,没有了雨,没有了云,没有了梦,没有了声音,没有了爱恋,没有了你。
github传送门: 在这里~
旋转卡壳
引入
我们之前讨论过了平面最近点对的\(O(nlogn)\)做法, 那我们考虑一下平面最远点对的做法.
首先暴力枚举复杂度是\(O(n^2)\)这个就不用说了.
我们联想到刚刚学习过的凸包.
很显然平面最远点对上的点都是凸包上的点.
我们枚举凸包上的点就能做到\(O(H^2)\)了.
这个在平均情况下是可以过的.
但是刻意卡一卡还是\(O(n^2)\)的.
考虑优化.
很容易发现, 最远点对寻找的是凸包的直径.
我们想象一下, 有一把游标卡尺紧紧卡住这个凸包, 要么贴住边要么卡住顶点, 围着凸包转一圈, 出现过的最大距离就是凸包的直径了. 也就是我们要求的平面最远点对的距离.
我们管这种东西叫旋转卡壳.
四个多音字. 共有\(2*3*2*2=24\)种可能的读音.
可怕的是"旋转"中"转"的读音都不能得到公认...
不过好像是读\(zhu\check an\)的多一些..
所以最后的读法应该是\(xu\acute an\ zhu\check an\ qi\check a\ k\acute e\)???
算了不重要...我们还是应该更关心是怎么个实现法.
分析
其实这个旋转卡壳的gif是很毒的, 我觉得大家都应该看一下, 所以就盗了一张图(滑稽)
我们将被一对卡壳正好卡住的对对应点称为对踵点(Antipodal point).
可以证明对踵点的个数不超过\(\frac3 2\)个, 也就是\(O(n)\)级别的.
那么如何找对踵点呢?
我们发现卡壳的情况有3种
-
卡住凸包的两个点.
-
卡住凸包的一个点和一条边.
-
特殊情况: 卡住凸包的一对平行边.
其中的第一种情况并不好处理, 我们主要考虑第二种, 而第三种则可以视为第二种的一种特殊情况.
我们考虑枚举边, 然后找与这个边距离最远的点. 将这个点与边的两个端点的距离取个最大值即可.
与边的距离我们就考虑三角剖分. 因为底边是定的(要枚举的), 所以高就与面积挂钩, 而面积直接用叉积就可以求了.. 又是凸多边形, 面积一定是正的..
但这看上去还是\(O(n^2)\)的啊..我们就需要考虑凸包优美的性质了.
比如面积是单峰的.
底一样了 高显然是单峰的, 所以面积也就是单峰的了.
所以我们枚举到点\(i\)时, 如果\(i+1\)对应的三角形的面积比\(i\)小, 我们就不需要枚举了.
不过这一分析好像暂时还并没有实质上影响到复杂度.我们继续观察, 枚举下一条边.
我们发现随着边的旋转, 距离最远的点不可能是刚才得到的最远点(绿)前面的点(红). 其实这也挺显然的.. 于是我们只需要从上一次找到的最高点开始枚举即可..
这样复杂度就降下来了.
代码
有一道板子题... Emmmm...
所以就贴一下完整的实现代码 (然而到了poj还是WA不知道为啥...
好吧用C++而不是G++就能AC了QAQ
#include <cmath>
#include <cstdio>
#include <algorithm>
const int N=50101;
const double eps=1e-9;
int dcmp(const double &a){
if(fabs(a)<eps)return 0;
return a<0?-1:1;
}
inline double max(const double &a,const double &b){return dcmp(a-b)>0?a:b;}
struct point{
double x,y;
point(const double &X=0,const double &Y=0):x(X),y(Y){}
}p[N],stk[N];int tp,mi;
point operator -(const point &a,const point &b){
return point(a.x-b.x,a.y-b.y);
}
double operator ^(const point &a,const point &b){
return a.x*b.x+a.y*b.y;
}
double operator *(const point &a,const point &b){
return a.x*b.y-a.y*b.x;
}
double len(const point &a){
return sqrt(a^a);
}
//bool cmpa(const point &a,const point &b){
// point X=point(1,0),A=a-p[0],B=b-p[0];
// double coa=(A^X)/len(A),cob=(B^X)/len(B);
// return dcmp(coa-cob)>0;
//} //按夹角排序(点积版)
bool cmpa(const point &a,const point &b){
point A=a-p[0],B=b-p[0];
if(!dcmp(A*B)) return dcmp(len(A)-len(B))>0;
return dcmp(A*B)>0;
} //叉积版
void grahamScan(point* p,int n){
std::sort(p+1,p+n,cmpa);
stk[++tp]=p[0]; stk[++tp]=p[1];
for(int i=2;i<n;++i){
while(dcmp((p[i]-stk[tp])*(stk[tp]-stk[tp-1]))>=0&&tp>2) --tp; //顺时针就退栈
stk[++tp]=p[i]; //进栈
}
}
double rotatingCalipers(){
int j=2; stk[tp+1]=stk[1]; double ans=-1e9;
for(int i=1;i<=tp;++i){
while(dcmp((stk[j+1]-stk[i])*(stk[i+1]-stk[i])-(stk[j]-stk[i])*(stk[i+1]-stk[i]))<0){ //这里的面积是负的哟~所以用的是小于..
++j; if(j>tp) j=1;
}
ans=max(ans,max(len(stk[j]-stk[i]),len(stk[j]-stk[i+1])));
}
return ans;
}
int main(){
int n; scanf("%d",&n); double my=1e9;
for(int i=0;i<n;++i){
scanf("%lf%lf",&p[i].x,&p[i].y);
if(dcmp(p[i].y-my)<0||
(!dcmp(p[i].y-my)&&dcmp(p[i].x-p[mi].x)<0))
my=p[i].y,mi=i;
} std::swap(p[0],p[mi]);
grahamScan(p,n);
double a=rotatingCalipers();
printf("%.0lf",a*a);
}
看上去非常麻烦读起来也非常麻烦的旋转卡壳写起来却只需要这么几行(说的是rotatingCalipers那个函数), 这就非常厉害了.
当然了, 旋转卡壳不仅仅可以用来求凸多边形的直径, 它的用途非常非常的广泛.
用途
凸多边形直径
分析
可以直接抄上面的求凸包直径...
代码
double diameterOfConvex(point* p,int n){
int j=1; stk[n]=stk[0]; double ans=-1e9;
for(int i=1;i<=tp;++i){
while(dcmp((p[j+1]-p[i])*(p[i+1]-p[i])-(p[j]-p[i])*(p[i+1]-p[i]))<0){
++j; if(j>tp) j=1;
}
ans=max(ans,max(len((p[j]-p[i]),len(p[j]-p[i+1])));
}
return ans;
}
凸多边形宽
分析
凸多边形的宽定义为平行切线的最小距离.
切线的话方向非常多, 但是要求最小的话, 我们不需要每个方向都检测.
很明显的, 如果这组平行线只卡住两个点(红), 我们总可以旋转一个角度, 使其中一条平行线与一条边重合, 从而找到更小的距离.
这很显然就是旋转卡壳的形式.
我们枚举每一条边, 找到距离最远的点时, 计算点到对边的距离, 然后找个最小值即可.
时间复杂度\(O(n)\).
代码
double widthOfConvex(point* p,int n){
double ans=1e9; p[n]=p[0]; int j=1;
for(int i=0;i<n;++i){
while(dcmp((p[j]-p[i])*(p[i+1]-p[i])-(p[j+1]-p[i])*(p[i+1]-p[i]))<0){
++j; if(j==n) j=0;
}
ans=min(ans,fabs((p[j]-p[i])*(p[i+1]-p[i])/len(p[i+1]-p[i])));
}
return ans;
}
凸多边形间最小距离
分析
这道题是有板子题的~戳这里查看..
讲道理
给定两个凸多边形\(A\)和\(B\), 要求找到两个点\(M,N\), 满足\(M\in A,N\in B\),求\(|MN|_{min}\)
当然这个是有前提的, 就是两个凸多边形不连接(比如不相交). 因为两个凸多边形的距离如果小于0的话根据定义最小距离自然就是0了, 这显然没什么意思.
事实上, 这个问题更为常见一些, 比如用来做碰撞检测(距离降为0)之类的, 所以理应有更多的算法. 似乎网上是能找到更多的解决方案的.
而今天的主角是旋转卡壳, 所以我们只说说旋转卡壳的做法.
首先很显然地, 我们可以发现最小距离的点对一定是在多边形的外部, 但并不一定在顶点上.
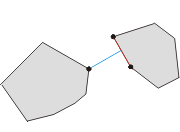
比如这张图上的点对中的一个就不是顶点, 而是红线和蓝线的交点.
我们让旋转的卡壳分别卡两个多边形..
我们枚举一个多边形的边, 然后从另一个多边形中找合适的对应点.
与上面不同的是, 因为要求距离最小, 所以找三角形面积最小的.
不过更新距离的时候要注意, 要分别更新每一条线段两个端点的到另一条线段的距离, 也就是4个距离取最小值防止遗漏. 就是说线段\(AB\)与线段\(CD\)的距离为
\(d=min(dis(A,CD),dis(B,CD),dis(C,AB),dis(D,AB))\).
代码
因为有板子题所以贴完整代码
其实交这个题的过程是很曲折的 而且baidu上有很多题解会WA...
#include <cmath>
#include <cstdio>
#include <algorithm>
const int N=1e4+10;
const double eps=1e-9;
int dcmp(const double &a){
if(fabs(a)<eps) return 0;
return a<0?-1:1;
}
struct point{
double x,y;
point(double X=0,double Y=0):x(X),y(Y){}
}p1[N],p2[N]; int y1min,y2min,y2max;
point operator -(const point &a,const point &b){return point(a.x-b.x,a.y-b.y);}
double operator *(const point &a,const point &b){return a.x*b.y-a.y*b.x;}
double operator ^(const point &a,const point &b){return a.x*b.x+a.y*b.y;}
inline double len(const point &a){return sqrt(a^a);}
inline double max(const double &a,const double &b){return dcmp(a-b)>0?a:b;}
inline double min(const double &a,const double &b){return dcmp(a-b)<1?a:b;}
inline void anticlockwise_sort(point *p,int n) {
for(int i=0;i<n-2;++i) {
double tmp=(p[i+2]-p[i])*(p[i+1]-p[i]);
if(dcmp(tmp)<0) return;
else if(dcmp(tmp)>0){
for(int i=0;i<n/2;++i){
point t=p[i];
p[i]=p[n-1-i];
p[n-1-i]=t;
}
}
}
}
double ptDisSeg(const point &p,const point &a,const point &b){
if(dcmp((p-a)^(b-a))<0) return len(p-a);
if(dcmp((p-b)^(a-b))<0) return len(p-b);
return fabs((p-a)*(b-a))/len(b-a);
}
double minDisSegs(const point &a,const point &b,const point &c,const point &d){
return min(min(ptDisSeg(c,a,b),ptDisSeg(d,a,b)),min(ptDisSeg(a,c,d),ptDisSeg(b,c,d)));
}
double minDistOfConvexs(point* p1,point *p2,int n1,int n2){
int j=0; double ans=1e9;
p1[n1]=p1[0]; p2[n2]=p2[0];
for(int i=0;i<n1;++i){
while(dcmp((p2[j]-p1[i])*(p1[i+1]-p1[i])-(p2[j+1]-p1[i])*(p1[i+1]-p1[i]))>0){
++j; if(j==n2) j=0;
}
ans=min(ans,minDisSegs(p1[i],p1[i+1],p2[j],p2[j+1]));
}
return ans;
}
int main(){
int n,m;
while(~scanf("%d%d",&n,&m)&&(n||m))
{
for(int i=0;i<n;++i)
scanf("%lf%lf",&p1[i].x,&p1[i].y);
for(int i=0;i<m;++i)
scanf("%lf%lf",&p2[i].x,&p2[i].y);
anticlockwise_sort(p1,n);
anticlockwise_sort(p2,m);
printf("%.5f\n",minDistOfConvexs(p1,p2,n,m));
}
}
凸多边形间最大距离
分析
分析完最小距离我们来说一下最大距离.
很明显, 这两个点不可能在凸多边形内.
一种很显然的想法是, 将两个凸包合并成一个大凸包, 然后求直径.
我们现在已经可以用\(O(nlogn)\)的时间复杂度完成这个任务了.
不过凸包的合并(在后面可能会学)好像是可以做到\(O(n)\)复杂度的.
不过好像也是利用了旋转卡壳的做法.
我们考虑能不能直接用旋转卡壳做.
由于可以等价为找大凸包上的对踵点, 所以用普通的旋转卡壳大约就可以做了.
枚举一个多边形的每一条边, 从另一个多边形中找距离最大的点, 然后用两个端点的距离的最大值更新即可.
代码
原理跟上面的都是大同小异的, 稍微拼一拼就出来了, 注意一下细节就ok了.
double maxDistOfConvexs(point* p1,point *p2,int n1,int n2){
int j=0; double ans=-1e9;
p1[n1]=p1[0]; p2[n2]=p2[0];
for(int i=0;i<n1;++i){
while(dcmp((p2[j]-p1[i])*(p1[i+1]-p1[i])-(p2[j+1]-p1[i])*(p1[i+1]-p1[i]))<0){
++j; if(j==n2) j=0;
}
ans=max(ans,max(len(p2[j]-p1[i+1]),len(p2[j]-p1[i])));
}
return ans;
}
这两个用途表示旋转卡壳不仅可以卡一个凸多边形, 还可以卡两个凸多边形, 进而解决一些问题.
最小面积矩形覆盖
分析
有一道板子题, 不过这题并不怎么好写OvO
然而有一种很好写的方法是输出9个nan(不知道是不是必须要看格式)就可以卡掉vfk大爷写的spj....
首先显然是求个凸包, 随便一扫描就行.
有一个看上去就很显然的结论, 也就是我们做这道题的关键, 就是矩形一定有一条边的一段是凸包的边.
所以我们考虑枚举这一条边.
如图所示. 我们现在枚举到了\(P'P\)这条边. 这时候直线\(l_1\sim l_4\)的斜率都已经确定了, 只需要至少确定一个顶点就可以唯一确定直线了.
那么相关的点自然就是\(Q,M,N\).
\(Q\)点我们已经能比较熟练的求出来了, 就是对踵点嘛. 但如何求\(M,N\)呢?
看到了垂直, 我们想到让每个顶点往\(\vec{PP_1}\)上做投影, 我们能很显然地看出投影的长度是单峰的.
我们旋转卡壳卡出最大值找到\(M\), 卡出最小值找到\(N\)就行了. 投影计算方法:
不过这里\(|\vec a|\)是常数, 我们只是比个大小没有必要算.
这样卡完我们就做完了.
然后就是处理题目中要求的各种蛋疼的输出..
- 长(可能是宽) 就是\(M,N\)在\(P'P\)上的投影之差
- 宽(可能是长) 就是\(Q\)到直线\(P'P\)的距离.
- 面积直接一波乘积就做完了, 而且可以化一波式子把平方去掉.
- 然后就是确定矩形的顶点了. 而我不会用计算几何的方式.
- 大约就是解析几何一样讨论一下斜率然后求交点乱搞就完了.
但是细节写起来好tm心态爆炸.
代码
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N=5e4+10;
const double eps=1e-9;
inline int dcmp(const double &a){
if(fabs(a)<eps) return 0;
return a<0?-1:1;
}
inline double max(const double &a,const double &b){return dcmp(a-b)>0?a:b;}
inline double min(const double &a,const double &b){return dcmp(a-b)<1?a:b;}
struct point{
double x,y;
point(double X=0,double Y=0):x(X),y(Y){}
}p[N],stk[N],ot[4]; int tp,n,mi;
inline point operator-(const point &a,const point &b){return point(a.x-b.x,a.y-b.y);}
inline double operator*(const point &a,const point &b){return a.x*b.y-a.y*b.x;}
inline double operator^(const point &a,const point &b){return a.x*b.x+a.y*b.y;}
inline double len(const point &a){return sqrt(a^a);}
bool cmpa(const point &a,const point &b){
point A=a-p[0],B=b-p[0];
if(!dcmp(A*B)) return len(A)>len(B);
return dcmp(A*B)>0;
}
bool cmpb(const point &a,const point &b){
if(!dcmp(a.y-b.y)) return dcmp(a.x-b.x)<0;
return dcmp(a.y-b.y)<0;
}
void scan(){
stk[++tp]=p[0]; stk[++tp]=p[1];
for(int i=2;i<n;++i){
while(dcmp((p[i]-stk[tp])*(stk[tp]-stk[tp-1]))>-1&&tp>2) --tp;
stk[++tp]=p[i];
}
}
double rotatingCalipers(){
int x=2,y=2,z=-1; stk[tp+1]=stk[1]; double ans=1e9,res=0;
for(int i=1;i<=tp;++i){
point edge=stk[i+1]-stk[i];
while(dcmp(edge*(stk[x]-stk[i])-edge*(stk[x+1]-stk[i]))<1){
++x; if(x>tp) x=1;
}
while(dcmp((edge^(stk[y]-stk[i]))-(edge^(stk[y+1]-stk[i])))<1){
++y; if(y>tp) y=1;
}
if(z==-1) z=x;
while(dcmp((edge^(stk[z]-stk[i]))-(edge^(stk[z+1]-stk[i])))>-1){
++z; if(z>tp) z=1;
}
res=edge*(stk[x]-stk[i])*(((stk[y]-stk[i])^edge)-((stk[z]-stk[i])^edge))/(edge^edge);
if(dcmp(res-ans)<0){
//更新答案
ans=res;
if(!dcmp(stk[i+1].x-stk[i].x)||!dcmp(stk[i+1].y-stk[i].y)){ //平行(垂直坐标轴)
double x1=min(min(stk[i].x,stk[x].x),min(stk[y].x,stk[z].x)),
x2=max(max(stk[i].x,stk[x].x),max(stk[y].x,stk[z].x)),
y1=min(min(stk[i].y,stk[x].y),min(stk[y].y,stk[z].y)),
y2=max(max(stk[i].y,stk[x].y),max(stk[y].y,stk[z].y));
ot[0]=point(x1,y1); ot[1]=point(x1,y2); ot[2]=point(x2,y1); ot[3]=point(x2,y2);
}
else{
double k1=(stk[i+1].y-stk[i].y)/(stk[i+1].x-stk[i].x),b1=stk[i].y-stk[i].x*k1,b11=stk[x].y-stk[x].x*k1,
k2=-1.0/k1,b2=stk[y].y-stk[y].x*k2,b22=stk[z].y-stk[z].x*k2,dk=k1-k2;
ot[0].x=(b2-b1)/dk; ot[0].y=ot[0].x*k1+b1;
ot[1].x=(b22-b1)/dk; ot[1].y=ot[1].x*k1+b1;
ot[2].x=(b2-b11)/dk; ot[2].y=ot[2].x*k1+b11;
ot[3].x=(b22-b11)/dk; ot[3].y=ot[3].x*k1+b11;
}
}
}
return ans;
}
int main(){scanf("%d",&n);
for(int i=0;i<n;++i){
scanf("%lf%lf",&p[i].x,&p[i].y);
if(dcmp(p[i].y-p[mi].y)<0||(!dcmp(p[i].y-p[mi].y)&&dcmp(p[i].x-p[mi].x)<0)) mi=i;
} swap(p[0],p[mi]); sort(p+1,p+n,cmpa);
scan();
double ans=rotatingCalipers();
printf("%.5lf\n",ans+eps);
sort(ot,ot+4,cmpb); p[0]=ot[0]; sort(ot+1,ot+4,cmpa);
for(int i=0;i<4;++i) printf("%.5lf %.5lf\n",ot[i].x+eps,ot[i].y+eps);
}
注意事项
这题这么难写所以就这么加了一个注意事项...
- 这个题卡\(N\)点的时候记得要从最高点后面枚举(不然就卡死在\(M\)点了)
- 旋转卡壳判断的时候一定要注意相等是可以的...
- 最后的输出还是有点扯淡.. 我采用了一种看上去很蠢的方式..
- 这个题卡精度(就是说你luogu呢), 输出的时候要加个eps再输出...(因为据说数据都是整数?)
所以说旋转卡壳里面用到了很多的凸包上的单调性, 要细心地找, 找到了还要细心地写..
学习计算几何的过程中也不要忘了解析几何因为保送不了, 高考还要考..
虽然计算繁杂了一点但是实在不知道怎么用向量表达的时候能做出题来啊..
反正数学考试也要写这种东西不是...
其他用途以后再学..


