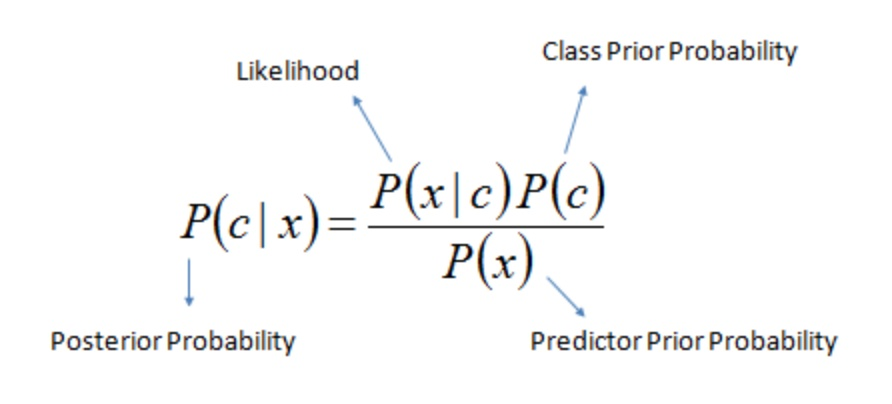
图中,x表示单个样本,c表示预测的类别
参考知乎
- 概率与似然
- 用贝叶斯 计算后验概率
- 机器学习-周志华
一、先验概率,条件概率与后验概率
先验概率是基于背景常识或者历史数据的统计得出的预判概率,一般只包含一个变量,例如,
。
条件概率是表示一个事件发生后另一个事件发生的概率,例如代表
事件发生后
事件发生的概率。
后验概率是由果求因,也就是在知道结果的情况下求原因的概率,例如Y事件是X引起的,那么就是后验概率,也可以说它是事件发生后的反向条件概率。
- 先验概率是由以往的数据分析得到的,而在得到信息后再重新加以修正的概率叫后验概率;
- 后验概率是反向条件概率,如果条件概率是有因求果,那么后验概率就是有果求因;
二、似然
概率模型的训练过程就是参数估计过程。(即估计事件发生的概率)
对于参数估计,统计学界的两个流派分别提供了不同的解决方案:
频率学派认为事件发生的概率是一个确定的值, 但是这个取值我们不知道。 我们可以通过t test 或者 p 值估计这个取值的范围。
贝叶斯学派认为事件的概率是一个分布, 我们通过观测到的数据对这一分布进行更新,从而得到更为准确的估计。
- 频率学派方案为:通过优化似然函数等准则来确定参数值(即未知的固定值)
极大似然估计 MLE
三、生成式模型与判别式模型
机器学习所要实现的是基于有限样本集尽可能准确地估计出后验概率 P(c | x)
大体来说,主要有两种策略:
- 给定x,通过直接建模P(c | x)来预测 c,这样得到的是“判别式模型”,例如:决策树、BP神经网络、SVM;
- 也可先对联合概率分布 P(x, c)建模,然后求得 P(c | x),这样得到的是“生成式模型”,例如:NB、HMM;
对于生成式模型,必然考虑
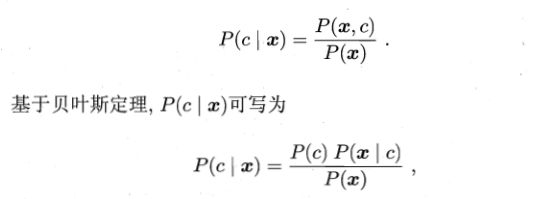

注: P(x)对所有类标记均相同




