向量数量积（点积）
向量内积
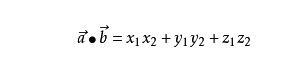
[x,y] = xTy
正交与线性无关
定理：若n维向量a1，a2，...，ar是一组两两正交的非零向量，则a1，a2，...，ar线性无关
基：向量空间中任意一个元素，都可以唯一地表示成基向量的线性组合。
规范正交基：n维向量是向量空间V的一个基，如果其中向量两两正交，且都是单位向量；
规范正交化：为一个基寻找与之等价的规范正交基的过程；方法：（基的规范正交化）施密特Schimidt正交化过程
正交矩阵：
满足 ATA=E 即A-1 = AT ，简称正交阵
A为正交阵的充要条件：A的列向量都是单位向量，且两两正交。
特征值与特征向量
设 A 是n阶方阵，如果存在数m和非零n维列向量 x，使得 Ax=mx 成立，则称 m 是A的一个特征值（characteristic value)或本征值（eigenvalue)。
非零n维列向量x称为矩阵A的属于（对应于）特征值m的特征向量或本征向量，简称A的特征向量或A的本征向量。
相似矩阵
若n阶矩阵A与B相似，则A与B的特征多项式相同，从而A与B的特征值亦相同；
推论：若n阶矩阵A与对角阵[r1 ...r n]相似，则r1 ...r n即是A的n个特征值；
对角化
n阶矩阵A与对角阵相似（A能对角化）的充要条件：A有n个线性无关的特征向量；
推论： 如果n阶矩阵A的n的特征值互不相等，则A与对角阵相似；
