常用模型:BP神经网络,RBF神经网络
一、神经元模型 | 连接权,阈值,激活函数

1. 输入信号通过带权重的连接(connection)进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,
然后通过“激活函数”处理以产生神经元的输出。#“激活函数”对应于图中f(.)
2. 激活函数理想中是阶跃函数,实际中常用连续可微的Sigmoid函数代替——
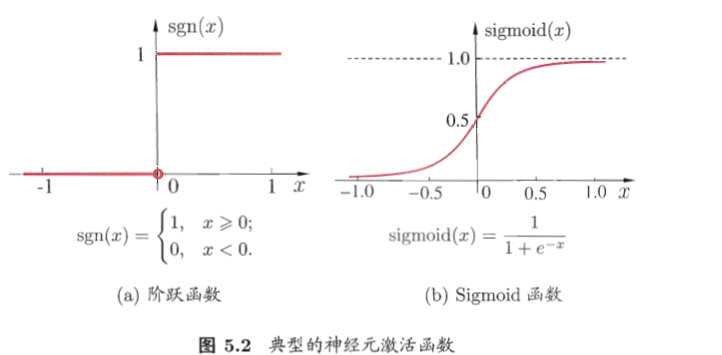
#神经元等价于“对数回归”模型
3. 把许多个神经元按一定的层次结构连接起来,就得到了神经网络。
从数学角度看,神经网络是
![]()
二、感知机与多层网络 | 如何解决非线性可分
1. 感知机由两层神经元组成(即不含隐层,只有输入、输出层)
2. 学习过程中,权重这样调整:

η∈(0, 1)称为学习率,控制每次更新的步长
3. 可以证明,样本若是线性可分的,则感知机的学习过程一定会收敛而求得适当的权重ω;
否则感知机学习过程将会发生振荡,不能求得合适解。
4. 解决非线性可分问题,需使用多层功能神经元,即含有“隐含层”神经元的网络
神经元之间不存在同层连接,也不存在跨层连接
这种结构称为“多层前馈神经网络”,前馈不是指信号不能向后传而是指网络拓扑结构上不存在环或回路;
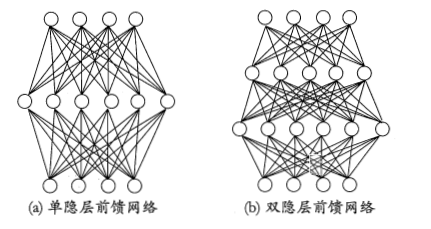
隐层与输出层包含功能神经元,图(a)通常称为“两层网络”
神经网络“学”到的东西,蕴涵在连接权重与阈值中。
#
SVM看成一种特殊的神经元模型:
- L-SVM本质上跟单神经元(即逻辑回归)模型的最大差别,只是代价函数的不同,所以可以将SVM也理解成一种神经元,只不过它的激活函数不是sigmoid函数,而是SVM独有的一种激活函数的定义方法。
- K-SVM只是比起L-SVM多了一个负责用于非线性变换的核函数,这个跟神经网络的隐层的思想也是一脉相承的。所以K-SVM实际上是两层的神经元网络结构:第一层负责非线性变换,第二层负责回归。
- 《基于核函数的SVM机与三层前向神经网络的关系》一文中,认为这两者从表达性来说是等价的。(注:这里的“三层前向神经网络”实际上是带一个隐层的神经网络,说是三层是因为它把网络的输入也看成一个层。
三、误差反向传播算法
BP神经网路,BP算法训练的多层前馈神经网络
1. 算法:通过输出误差(y'-y)反向去调整权重ωi(和阈值)
BP是一个迭代学习算法
1)学习率η控制迭代中的更新步长,太大容易振荡,太小收敛速度过慢;
2)BP算法基于梯度下降策略,对参数ω进行调整,对误差Ek,给定学习率η,有

3)迭代过程循环进行,知道达到某些停止条件,例如训练误差已达到一个很小的值;
2. 如何选择隐层神经元个数?
可以证明,只需一个包含足够多神经元的隐层,多层前馈网络就能以任意精度逼近任意复杂度的连续函数。
如何选择隐层神经元个数仍是未决问题,实际中靠“试错法”
3.缓解BP网络过拟合的策略
1)“early stopping”,将数据分成训练集和验证集,训练集来计算梯度、更新连接权和阈值,验证集用来估计误差,若训练集误差降低但验证集误差升高,则停止训练,同时返回具有最小验证集误差的连接权和阈值
2)“正则化”:在误差目标函数中增加一个用于描述网络复杂度的部分
四、全局最小与局部极小
优化:对于神经网络在训练集上的误差E,调整连接权ω和阈值θ,使得E全局最小
但是基于梯度的搜索,在局部极小值停止
采用以下方法试图“跳出”局部极小,逼近全局最小——
1)以多组不同参宿初始化多个神经网络,训练后取误差最小的解作为最终参数
2)“模拟退火”技术:以逐渐缩小的概率接受“次优解”
3)使用随机梯度下降
4)遗传算法
五、其他常见神经网络
RBF:两层网络,使用径向基/高斯函数作为激活函数,能以任意精度逼近任意连续函数
#优点——非线性拟合能力强;局部逼近;具有唯一最佳逼近的特性,且无局部极小问题存在;收敛速度快;结构简单
RBF: 的神经元是一个以gaussian函数为核函数的神经元。
Radial basis function: .
x 是自变量, b: 是bias,一般为固定常数,决定Gaussian函数的宽度。参数意义(对应于libsvm中的gamma)
w:weight (权重),决定Gaussian 函数的中心点,是一个可变常数。
输出结果: 不再是非0 即1,而是一组很smooth的小数,在特定的weight处具有最大的函数值。

“感知域” —— receptive field.
一个神经元,只负责对某一块局部进行响应。速度当然快得多。
ART
SOM
级联相关网络:结构自适应,网络的结构也当作学习的目标之一
六、深度学习
1.模型:很深层的神经网络
2. 如何训练?——难以直接用经典的BP算法训练
解决:“无监督逐层训练”,也即“预训练+微调”;
或者“权共享”策略,典型是CNN
补充:
神经网络是一种很难解释的“黑箱模型”


