开发库:
SVM难点:核函数选择
一、基本问题
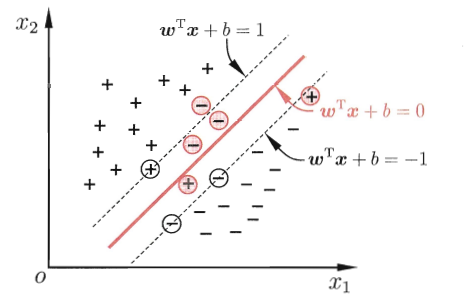
找到约束参数ω和b,支持向量到(分隔)超平面的距离最大;此时的分隔超平面称为“最优超平面”
距离表示为,
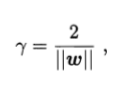
问题表示为,
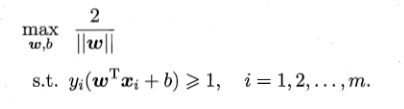
#支持向量机名字的由来:由支持向量得到的分类器
二、问题的求解
上述问题为一个凸二次优化问题,可以由现成的优化计算包求解
高效方法:用拉格朗日乘子法求解其对偶问题,得到问题的解——
SMO算法:在参数初始化后,

![]()
SMO算法之所以高效,由于在固定其他参数后,仅优化两个参数(αi和αj)能做到非常高效。
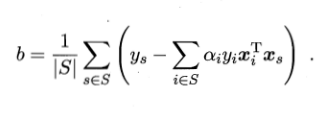
b使用所有支持向量求解的平均值
三、核函数
问题:现实中,样本空间也许并不存在一个能正确划分两类样本的超平面。
如果原始空间是有限维(即属性有限),那么一定存在一个高维特征空间使样本可分。
#核函数:用来等效原始空间到高维空间的映射,为了实现两类样本线性可分
要求样本在特征空间线性可分,则特征空间的好坏对支持向量机的性能至关重要。

假设这样一个函数:
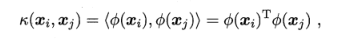
求解后可以得到
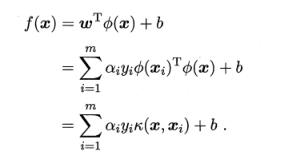
上式称为“支持向量展式”,κ(.,.)就是核函数
通常Φ(.)的具体形式是未知的
在不知道特征映射的形式时,我们并不知道什么样的核函数是合适的,而核函数也仅是隐式地定义了这个特征空间。
于是,“核函数选择”称为支持向量机的最大变数。

此外,还可以通过函数组合得到“核函数”。
四、软间隔与正则化
样本空间或者特征空间中一定线性可分?
1. 很难确定某个核函数使得训练样本在特征空间中线性可分
2. 线性可分的结果是不是由于过拟合造成的
问题的解决——
“软间隔”:允许支持向量机在一些样本上出错
优化目标改写为:
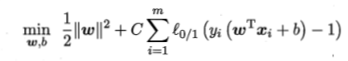
C称为正则化常数(惩罚因子),l0/1表示损失函数,C为有限值时上式允许一些样本不满足约束
正则化可理解为一种“罚函数法”,即对不希望得到的结果施以惩罚,从而使得优化过程趋向于希望目标。
“正则化”regularization问题:
推导发现“软间隔”问题,一方面与用户希望获得何种性质的模型有关;另一方面降低了最小化训练误差的过拟合风险;
五、支持向量回归SVR
SV Regression
f(x)与y之间差的绝对值小于等于ε,则认为被预测正确。
六、核方法
给定训练样本,学得的模型总能表示成核函数的线性组合。
那么,核方法指——引入核函数来将线性学习器拓展为非线性学习器。
“核线性判别分析”
补充阅读:
1. 支持向量机的求解通常借助于凸优化技术
2. 非线性核SVM的时间复杂度理论上不低于O(m^2),研究重点是设计快速近似算法
3. 线性核SVM常用于分析大规模数据
4. 多核学习使用多个核函数并通过学习获得最优凸组合作为最终的核函数,实际是一种集成学习机制
补充++


