一、基本形式
通过属性的线性组合来进行预测,
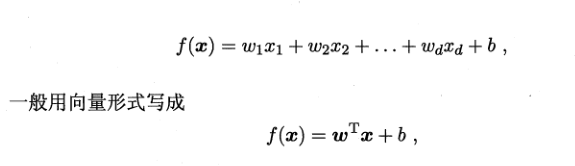
许多非线性模型可以在线性模型的基础上,引入层级结构或高维映射而得。
二、线性回归
最小二乘法:求解ω和b;(即均方误差最小化)
多元线性回归:样本由多个属性描述,即x为多维向量;
若矩阵不满秩产生多个解,解决方法:引入正则化项;(即增加约束)
三、对数/逻辑线性回归
广义线性模型:

g(.)条件:连续且充分光滑(单调可微)
为了预测值连续,引入Sigmoid函数
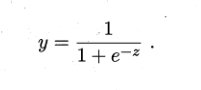
得到,
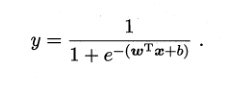
极大似然估计:求解ω和b
四、线性判别分析LDA
也叫“Fisher判别”
将样例投影到一条直线上,使同类样例投影点尽可能接近,异类样例投影点尽可能远离;
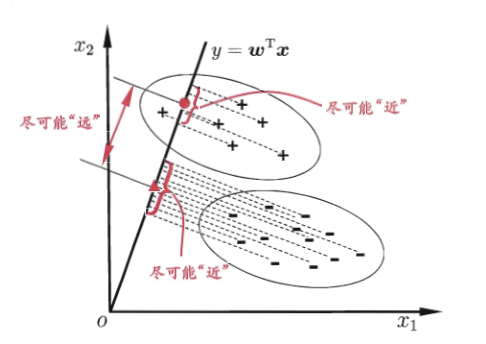
五、多分类策略
“一对一” one vs one 共训练N(N-1)/2个分类器,投票 (其中N为类别数)
“一对其余” one vs rest/ one vs all 共训练N个分类器,投票
“多对多”
六、类别不平衡问题
假设 正例<反例
“再平衡”“再缩放”:根据正、反例比例调节阈值
对反例“欠采样”
对正例“过采样”
注意:这里“欠采样”与“过采样”均有专门算法,不能简单“随机丢弃”或者“随机重复”。
#逻辑回归即LR;
多元回归,若要考虑特征之间的相互关系,著名的有FM模型;


