数字根(digital root)

　　

　　来源：LeetCode 258  Add Dights

　　Question：Given a non-negative integer  num , repeatedly add all its digits until the result has only one digit.

　　For example:

　　　　　Given  num = 38 , the process is like:  3 + 8 = 11 ,  1 + 1 = 2 . Since  2  has only one digit, return it.

　　Follow up:
　　　　　Could you do it without any loop/recursion in O(1) runtime?

 

　　分析：

　　数字根(digital root)是自然数的一种性质，即每个自然数都有一个数字根。数根是将一自然数的各个位数相加(即横向相加)，若加完后的值大于等于10的话，则继续将各位数进行横向相加直到其值小于10为止。例如54817的数根为7，因为5+4+8+1+7=25，25大于10则再加一次，2+5=7，7小于10，则7为54817的数字根。

　　上面问题即是求一个非负整数的数字根。很容易想到下面这种方法解决问题：

#include<stdio.h>
#include<assert.h>

int addDigits(int num) 
{
    int temp=0;
    while(num>=10)
    {
        temp+=(num%10);
        num/=10;
    }
    temp+=num;        //不要忽略最高位数
    num=temp;
    if(num>=10)
    {
        num=addDigits(num);//num仍大于10，则递归调用addDights函数
    }
    return num;
}

int main()
{
    int num;
    scanf("%d",&num);
    assert(num>=0);    //非负整数断言
    printf("%d\n",addDigits(num));
    return 0;
}

 

　　注意题目的延伸：要求我们不使用循环/递归复杂度O(1)

　　这里用到一个求数字根的公式：　　　　

　　　　　　　　　　　　　

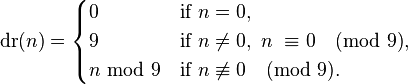
　　上述公式的文字表述为：0的数字根为0，9的倍数的数字根为9，其他自然数的数字根为其除以9的余数。证明过程点击这里

　　

　　上述公式可简单表述为：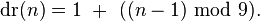

　　

　　所以对于延伸的问题我们可以写出解决方法如下：

#include<stdio.h>
#include<assert.h>

int addDigits(int num) 
{
    return 1+(num-1)%9;        //直接调用公式
}

int main()
{
    int num;
    scanf("%d",&num);
    assert(num>=0);    //非负整数断言
    printf("%d\n",addDigits(num));
    return 0;
}