算法篇——果园里的树

 

　　来源：《算法竞赛入门经典》例题5.4.3

　　题目：果园里的树排列成矩阵。它们的x和y坐标均是1~99的整数。输入若干个三角形，依次统计每一个三角形内部和边界上共有多少棵树

　　样例输入：

　　1.5 1.5　　  1.5 6.8　　 6.8 1.5

　　10.7 6.9　　8.5 1.5　　 14.5 1.5

　　样例输出：

　　15

　　17

　　分析：

　　三角形的有向面积：

double area2(double x0,double y0,double x1,double y1,double x2,double y2)
{
    return x0*y1+x2*y0+x1*y2-x2*y1-x0*y2-x1*y0;
}

 

　　上面得到的是以A(x0,y0)，B(x1,y1)，C(x2,y2)为定点的三角形的有向面积的2倍

　　如果area≥0，则说明ABC三点呈现逆时针排列；

　　如果area=0，则ABC三点共线；

　　如果area≤0，则说明ABC三点呈现顺时针排列。

　　假设输入三角形为ABC，点O在三角形ABC内部或边界上当且仅当S_ABC=S_OAB+S_OBC+S_OCA，所以我们只需遍历坐标系中所有的点判定是否在三角形内部或边界上即可。

　　需要注意的是：在判断两个浮点数a和b是否相等时，请尽量判断fabs(a-b)是否小于一个极小的数（求浮点数的绝对值要用fabs，求整数绝对值用abs），如1e-9（C语言中的浮点数，表示1*10^-9）

　　源码：

#include<stdio.h>
#include<math.h>

double area2(double x0,double y0,double x1,double y1,double x2,double y2)//算出三角形有向面积的2倍
{
    return x0*y1+x2*y0+x1*y2-x2*y1-x0*y2-x1*y0;
}

int main()
{
    double x0,y0,x1,y1,x2,y2,S1,S2,S3,S;
    int x,y,n;            //n表示三角形内部和边界上树的数量
    while(scanf("%lf%lf%lf%lf%lf%lf",&x0,&y0,&x1,&y1,&x2,&y2)==6)
    {
        n=0;
        S=fabs(area2(x0,y0,x1,y1,x2,y2));
        for(x=1;x<=99;x++)
        {
            for(y=1;y<=99;y++)
            {
                S1=fabs(area2(x*1.0,y*1.0,x0,y0,x1,y1));
                S2=fabs(area2(x*1.0,y*1.0,x1,y1,x2,y2));
                S3=fabs(area2(x*1.0,y*1.0,x2,y2,x0,y0));
                if(fabs(S-S1-S2-S3)<1e-9)   //判断树是否在三角形的内部或者边界上
                    n++;
            }
        }
        printf("%d\n",n);
    }

    return 0;
}

 

　　另外，对于上述问题有的人会想到用海伦公式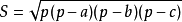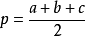：   ，       来计算，但在使用时需要小心浮点误差（前面的area2只有加减法和乘法，而海伦公式中却有除法和开平方）。

　　如果三角形的三个点A，B，C是按照统一方向（顺时针或逆时针）输入的话，我们还可以根据有向面积S_OAB，S_OBC和S_OCA的符号判断O是否在在三角形内部或边界上（三个三角形的有向面积互不异号）。