笔记:红黑树旋转和插入
红黑树
红黑树是每个节点都带有颜色属性的二叉查找树,颜色或红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 性质1. 节点是红色或黑色。
- 性质2. 根节点是黑色。
- 性质3. 每个叶节点(NIL节点,空节点)是黑色的。
- 性质4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
旋转
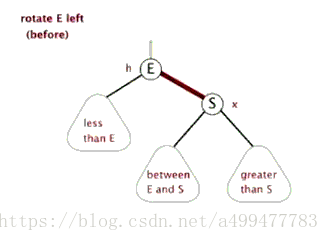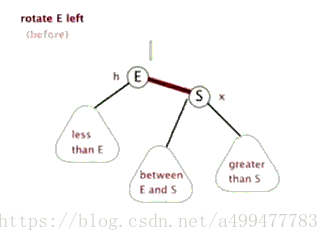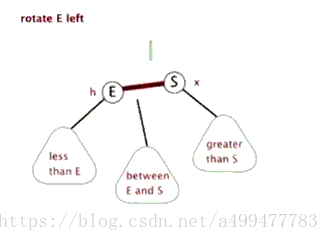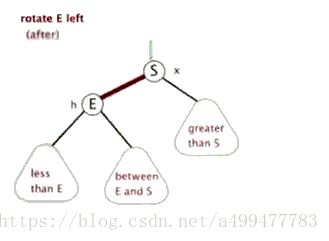
左旋
/**
* 左旋,
* @param current
*/
private void rotateLeft(Node current) {
Node right = current.rightChild;
Node temp = right.leftChild;
right.leftChild = current;
current.rightChild = temp;
}右旋
/**
* 右旋
* @param current
*/
private void rotateRight(Node current) {
Node left = current.leftChild;
Node temp = left.rightChild;
left.rightChild = current;
current.leftChild = temp;
}红黑树的插入
插入过程和二叉树的插入过程相同,先找到插入的节点然后插入。不同的是在插入后,需要通过旋转和着色操作,使红黑树满足规则,即满足黑色平衡。
插入一个节点
/**
* 插入一个节点
* @param node
* @return
*/
public void insertNode(Node node) throws KeyAlreadyExistsException {
if (root == null) {
node.color = NodeColor.BLACK;
root = node;
} else {
Stack<Node> parentStack = new Stack<Node>();
Node current = root;
while (current != null) {
parentStack.push(current);
if (node.isBiggerThan(current)) {
current = current.rightChild;
} else if (node.isSmallerThan(current)){
current = current.leftChild;
} else {
throw new KeyAlreadyExistsException("this key is already exists!!!");
}
}
Node parent = parentStack.peek();
if (node.isBiggerThan(parent)) {
parent.rightChild = node;
} else {
parent.leftChild = node;
}
//调整使树平衡
insertFixUp(parentStack, node);
}
}调整和着色
插入新节点时,默认新节点为红色节点。于是有如下两种情况:
1. 父节点为黑色,满足黑色平衡,不需要进行调整。
2. 父节点为红色,不满足规则,需要进行调整。
当插入节点的父节点为红色时,出现连续红色节点,不满足性质4,因此需要调整。调整时分为如下两种情况:
1. 插入节点的叔叔节点为红色,此时需要通过着色操作,将父节点和叔叔节点变为黑色,并将祖父节点变为红色,将祖父节点作为“当前节点”。并继续对“当前节点”进行调整。
2. 插入节点的叔叔节点为黑色,需要进行旋转,使树满足规则。
针对上面的第二种情况,也就是叔叔节点为黑色时,可分为如下两种情况进行旋转。
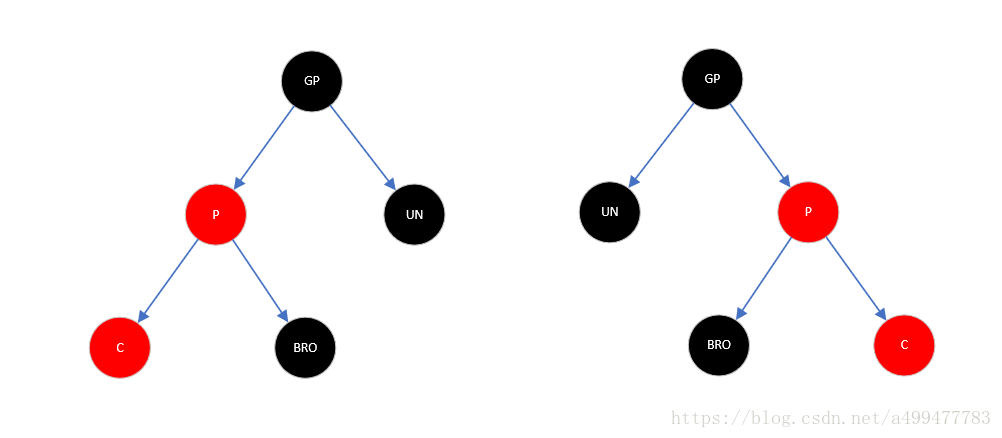
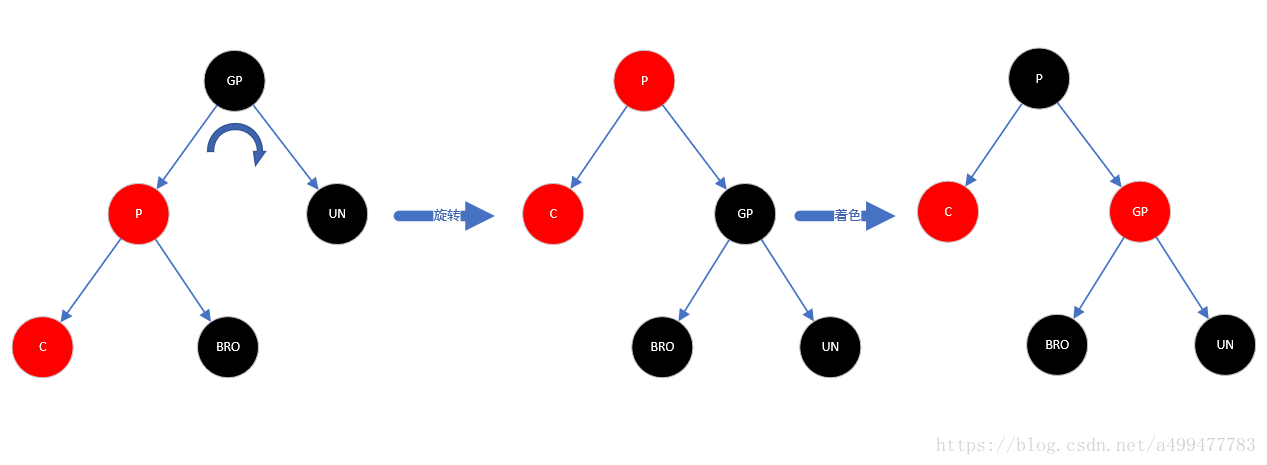
1、插入节点在外侧(插入节点和父节点方向相同:同在左侧、同在右侧),如下图所示:
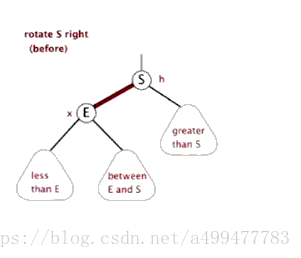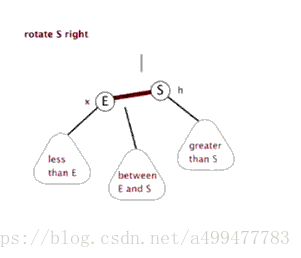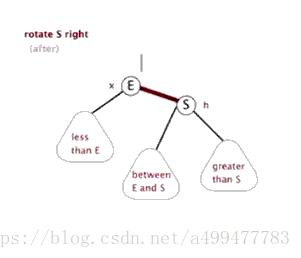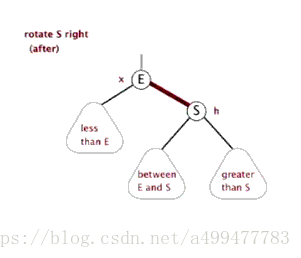
对于这种情况,只需要对祖父节点进行一次旋转即可修正。以祖父节点为轴向插入节点一侧的相反方向旋转一次,然后将原父节点颜色置为黑色,将原祖父节点颜色置为红色。即可满足所有的性质。这里以插入节点在左侧为例,先将祖父节点右旋(插入节点的相反方向),然后将原父节点置为红色,祖父节点置为黑色。调整后,满足所有性质。
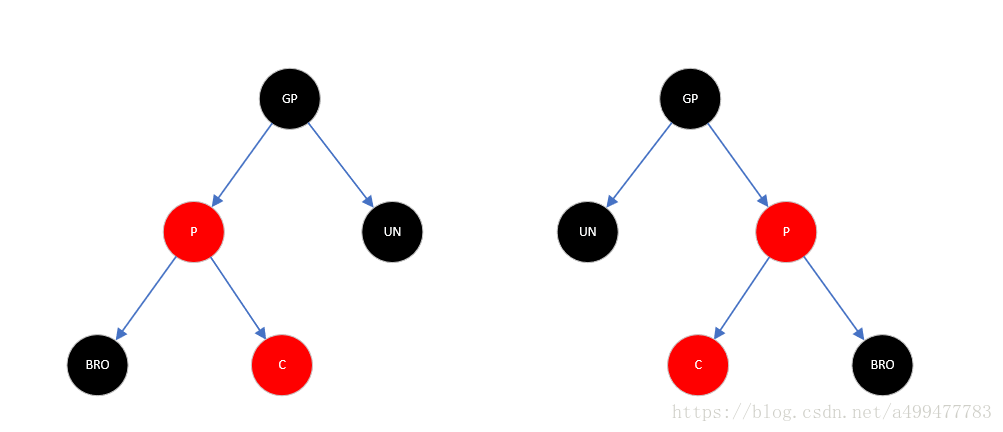
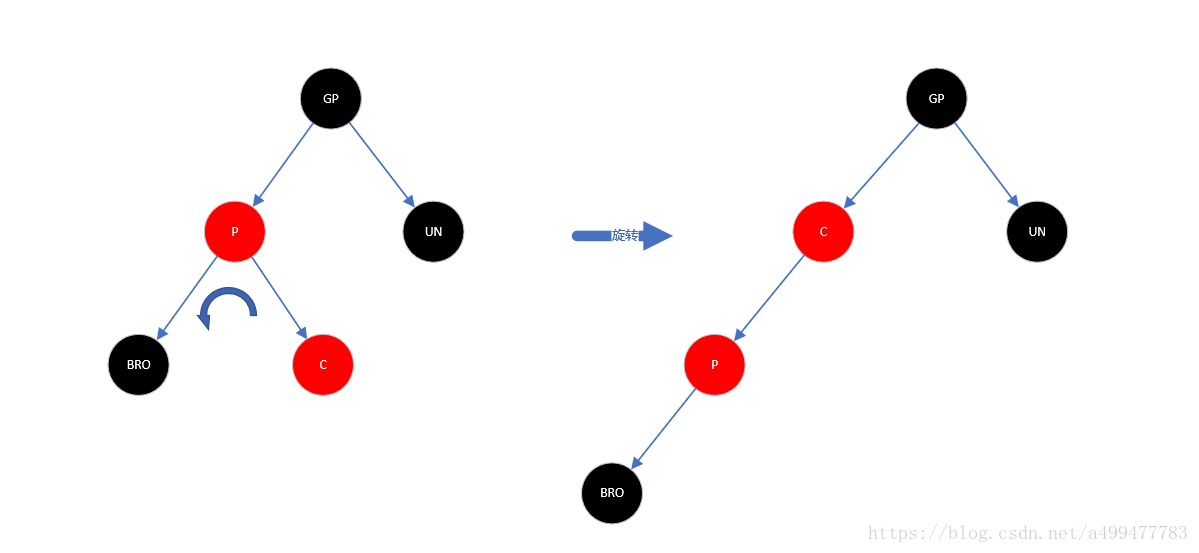
2、 插入节点在内侧(插入节点和父节点方向相反),如下图所示:
对于插入节点在内侧的情况,可以以父节点为轴,向相反方向旋转一次。然后将原父节点作为“当前节点”,于是就变为情况1,进行情况1的操作即可。这里以插入节点在右侧为例,以父节点为轴,左旋一次。然后以父节点为当前节点,变为情况1。
对于以上情况,在旋转时需要用到父节点和祖父节点,将旋转过的子树与原树连接,还需要用到增祖父节点。因此,如果节点中没有存放父节点的信息时,建议将使用栈来存放当前节点的所有祖先节点。调整树的代码如下:
/**
* 调整红黑树,使其满足黑色高度相同
* @param parentStack
* @param newNode
*/
private void insertFixUp(Stack<Node> parentStack, Node newNode) {
Node parent = parentStack.pop();
Node current = newNode;
Node uncle = null;
Node gParent = null;
while (parent != null) {
//父节点黑色
if (parent.isBlack()) {
return ;
}
gParent = parentStack.pop();
uncle = gParent.getAnotherChild(parent);
if (uncle != null && uncle.isRed()) {
uncle.color = NodeColor.BLACK;
parent.color = NodeColor.BLACK;
gParent.color = NodeColor.RED;
current = gParent;
if (parentStack.empty()) {
current.color=NodeColor.BLACK;
parent = null;
} else {
parent = parentStack.pop();
}
} else {
// uncle is null or uncle is black, rotate and break while
//情况1:插入节点在内侧时,反向旋转父节点,使其到外侧,变为情况2
if (parent.isLeftOf(gParent) && current.isRightOf(parent)) {
rotateLeft(parent);
gParent.leftChild = current;
current = parent;
parent = gParent.leftChild;
} else if (parent.isRightOf(gParent) && current.isLeftOf(parent)) {
rotateRight(parent);
gParent.rightChild = current;
current = parent;
parent = gParent.rightChild;
}
//情况2:插入节点在外侧时,反向旋转祖父节点,完成调整
if (parent.isRightOf(gParent) && current.isRightOf(parent)) {
rotateLeft(gParent);
gParent.color = NodeColor.RED;
parent.color = NodeColor.BLACK;
current = parent;
} else if (parent.isLeftOf(gParent) && current.isLeftOf(parent)) {
rotateRight(gParent);
gParent.color = NodeColor.RED;
parent.color = NodeColor.BLACK;
current = parent;
}
parent = null;
}
} // end while
if (parentStack.empty()) {
root = current;
}
if (!parentStack.empty()){
if (gParent.isRightOf(parentStack.peek())){
parentStack.peek().rightChild = current;
} else {
parentStack.peek().leftChild = current;
}
}
}