数据预处理规则
数据预处理在众多深度学习算法中都起着重要作用。实际情况中,将数据做归一化和白化处理后,很多算法能够发挥最佳效果。但是预处理的精确参数并非显而易见,一般需要尝试。
1.数据归一化
数据预处理中标准的第一步是数据归一化。这一步通常视具体情况选择。归一化的一般方法有如下3种:
1.简单缩放 2.逐样本均值消减(也称为移除直流分量) 3.特征标准化(使数据集中所有特征都具有零均值和单位方差)
1.1简单缩放
目的是通过对数据的每一个维度的值进行重新调节(这些维度可能是相互独立的),使得最终的数据向量落在 [0,1]或[ − 1,1] 的区间内(根据数据情况而定)。这对后续的处理十分重要,因为很多默认参数(如 PCA-白化中的 epsilon)都假定数据已被缩放到合理区间。
例如在处理自然图像时,我们获得的像素值在 [0,255] 区间中,常用的处理是将这些像素值除以 255,使它们缩放到 [0,1] 中。
Matlab函数mapminmax: x为向量。[y,ps]=mapminmax(x)。默认映射范围为[-1,1]。ps为映射规则,y为映射结果。可以对ps进行设置 ps.ymin和ps.ymax。然后进行自定义范围映射,当然可以把对本样本的ps规则应用到其他样本,如[y,ps]=mapminmax['apply',x1,ps]。实际映射方程y = (ymax-ymin)*(x-xmin)/(xmax-xmin) + ymin。
其他的缩放机制还有atan,log等。具体参考常见的样本数据归一化。
1.2逐样本均值消减
如果数据平稳(即数据每一个维度的统计都服从相同分布),可以在每个样本上减去数据的统计平均值。
例子:对于图像,这种归一化可以移除图像的平均亮度值 (intensity)。很多情况下我们对图像的照度并不感兴趣,而更多地关注其内容,这时对每个数据点移除像素的均值是有意义的。注意:虽然该方法广泛地应用于图像,但在处理彩色图像时需要格外小心,具体来说,是因为不同色彩通道中的像素并不都存在平稳特性。
Matlab中对应使用mean()函数求均值。
1.3特征标准化
特征标准化指的是(独立地)使得数据的每一个维度具有零均值和单位方差。这是归一化中最常见的方法并被广泛地使用(例如,在使用支持向量机(SVM)时,特征标准化常被建议用作预处理的一部分)。在实际应用中,特征标准化的具体做法是:首先计算每一个维度上数据的均值(使用全体数据计算),之后在每一个维度上都减去该均值。下一步便是在数据的每一维度上除以该维度上数据的标准差。
例子:处理音频数据时,常用 Mel 倒频系数 MFCCs 来表征数据。然而MFCC特征的第一个分量(表示直流分量)数值太大,常常会掩盖其他分量。这种情况下,为了平衡各个分量的影响,通常对特征的每个分量独立地使用标准化处理。、
在Matlab里面,用于归一化的方法有premnmx、postmnmx、tramnmx ;prestd、poststd、trastd。其中premnmx指的是归一到[-1 1],而prestd归一到单位方差和零均值。
2.PCA和ZCA白化
在做完简单的归一化后,白化通常会被用来作为接下来的预处理步骤,它会使我们的算法工作得更好。实际上许多深度学习算法都依赖于白化来获得好的特征。在进行 PCA/ZCA 白化时,首先使特征零均值化是很有必要的,这一步需要在计算协方差矩阵前完成。(唯一例外的情况是已经进行了逐样本均值消减,并且数据在各维度上或像素上是平稳的。)
接下来在 PCA/ZCA 白化中我们需要选择合适的 epsilon(回忆一下,这是规则化项,对数据有低通滤波作用)。选取合适的 epsilon 值对特征学习起着很大作用,下面讨论在两种不同场合下如何选取 epsilon:
2.1基于重构的模型
在基于重构的模型中(包括自编码器,稀疏编码,受限 Boltzman 机(RBM),k-均值(K-Means)),经常倾向于选取合适的 epsilon 以使得白化达到低通滤波的效果。(译注:通常认为数据中的高频分量是噪声,低通滤波的作用就是尽可能抑制这些噪声,同时保留有用的信息。
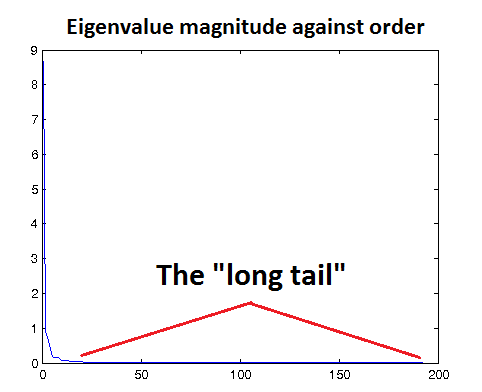
在 PCA 等方法中,假设数据的信息主要分布在方差较高的方向,方差较低的方向是噪声(即高频分量),因此后文中 epsilon 的选择与特征值有关)。一种检验epsilon 是否合适的方法是用该值对数据进行 ZCA 白化,然后对白化前后的数据进行可视化。如果 epsilon 值过低,白化后的数据会显得噪声很大;相反,如果 epsilon 值过高,白化后的数据与原始数据相比就过于模糊。一种直观上得到 epsilon 大小的方法是以图形方式画出数据的特征值,如下图的例子所示,你可以看到一条"长尾",它对应于数据中的高频噪声部分。你需要选取合适的 epsilon,使其能够在很大程度上过滤掉这条"长尾",也就是说,选取的 epsilon 应大于大多数较小的、反映数据中噪声的特征值。
在基于重构的模型中,损失函数有一项是用于惩罚那些与原始输入数据差异较大的重构结果(译注:以自动编码机为例,要求输入数据经过编码和解码之后还能尽可能的还原输入数据)。如果 epsilon 太小,白化后的数据中就会包含很多噪声,而模型要拟合这些噪声,以达到很好的重构结果。因此,对于基于重构的模型来说,对原始数据进行低通滤波就显得非常重要。
提示:如果数据已被缩放到合理范围(如[0,1]),可以从epsilon = 0.01或epsilon = 0.1开始调节epsilon。
2.2基于正交化的ICA模型
对基于正交化ICA(独立主元分析)的模型来说,保证输入数据尽可能地白化(即协方差矩阵为单位矩阵)非常重要。这是因为:这类模型需要对学习到的特征做正交化,以解除不同维度之间的相关性(详细内容请参考 ICA 一节)。因此在这种情况下,epsilon 要足够小(比如 epsilon = 1e − 6)。
提示:我们也可以在PCA白化过程中同时降低数据的维度。这是一个很好的主意,因为这样可以大大提升算法的速度(减少了运算量和参数数目)。确定要保留的主成分数目有一个经验法则:即所保留的成分的总方差达到总样本方差的 99% 以上。(详细内容请参考PCA )
注意: 在使用分类框架时,我们应该只基于练集上的数据计算PCA/ZCA白化矩阵。需要保存以下两个参数留待测试集合使用:(a)用于零均值化数据的平均值向量;(b)白化矩阵。测试集需要采用这两组保存的参数来进行相同的预处理。
3.具体应用注意事项
❶大图像。采用基于 PCA/ZCA 的白化方法是不切实际的,因为协方差矩阵太大。在这些情况下我们退而使用 1/f 白化方法。
❷自然灰度图像。具有平稳特性,我们通常在第一步对每个数据样本分别做均值消减(即减去直流分量),然后采用 PCA/ZCA 白化处理,其中的 epsilon 要足够大以达到低通滤波的效果。
❸彩色图像,色彩通道间并不存在平稳特性。因此我们通常首先对数据进行特征缩放(使像素值位于 [0,1] 区间),然后使用足够大的 epsilon 来做 PCA/ZCA。注意在进行 PCA 变换前需要对特征进行分量均值归零化。
❹音频数据 (MFCC 和频谱图),每一维度的取值范围(方差)不同。例如 MFCC 的第一分量是直流分量,通常其幅度远大于其他分量,尤其当特征中包含时域导数 (temporal derivatives) 时(这是音频处理中的常用方法)更是如此。因此,对这类数据的预处理通常从简单的数据标准化开始(即使得数据的每一维度均值为零、方差为 1),然后进行 PCA/ZCA 白化(使用合适的 epsilon)。
❺MNIST手写数字。数据集的像素值在 [0,255] 区间中。我们首先将其缩放到 [0,1] 区间。实际上,进行逐样本均值消去也有助于特征学习。注:也可选择以对 MNIST 进行 PCA/ZCA 白化,但这在实践中不常用。
4.中英文对照
归一化 normalization 白化 whitening 直流分量 DC component 局部均值消减 local mean subtraction 消减归一化 sparse autoencoder 缩放 rescaling 逐样本均值消减 per-example mean subtraction 特征标准化 feature standardization 平稳 stationary Mel倒频系数 MFCC 零均值化 zero-mean 低通滤波 low-pass filtering 基于重构的模型 reconstruction based models 自编码器 autoencoders 稀疏编码 sparse coding 受限Boltzman机 RBMs k-均值 k-Means 长尾 long tail 损失函数 loss function 正交化 orthogonalization
本文参考:
1.数据预处理 2.数据归一化汇总
其中,参考2给出了ANN中奇异样本预处理的代码。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号