逻辑回归

比较好的逻辑回归博客：逻辑回归

本栏目（Machine learning）包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM（Support Vector Machines 支持向量机）、聚类、降维、异常检测、大规模机器学习等章节。所有内容均来自Standford公开课machine learning中Andrew老师的讲解。（https://class.coursera.org/ml/class/index）

第三讲-------Logistic Regression & Regularization

本讲内容：

Logistic Regression

=========================

(一)、Classification

（二）、Hypothesis Representation

（三）、Decision Boundary

（四）、Cost Function

（五）、Simplified Cost Function and Gradient Descent

（六）、Parameter Optimization in Matlab

（七）、Multiclass classification : One-vs-all

The problem of overfitting and how to solve it

=========================

（八）、The problem of overfitting

（九）、Cost Function

（十）、Regularized Linear Regression

（十一）、Regularized Logistic Regression

本章主要讲述逻辑回归和Regularization解决过拟合的问题，非常非常重要，是机器学习中非常常用的回归工具，下面分别进行两部分的讲解。

第一部分：Logistic Regression

/*************（一）~（二）、Classification / Hypothesis Representation***********/

假设随Tumor Size变化，预测病人的肿瘤是恶性（malignant）还是良性（benign）的情况。

给出8个数据如下：

   

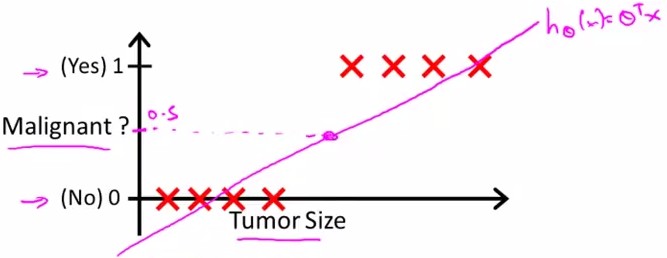
假设进行linear regression得到的hypothesis线性方程如上图中粉线所示，则可以确定一个threshold:0.5进行predict

y=1, if h(x)>=0.5

y=0, if  h(x)<0.5

即malignant=0.5的点投影下来，其右边的点预测y=1;左边预测y=0；则能够很好地进行分类。

那么，如果数据集是这样的呢？

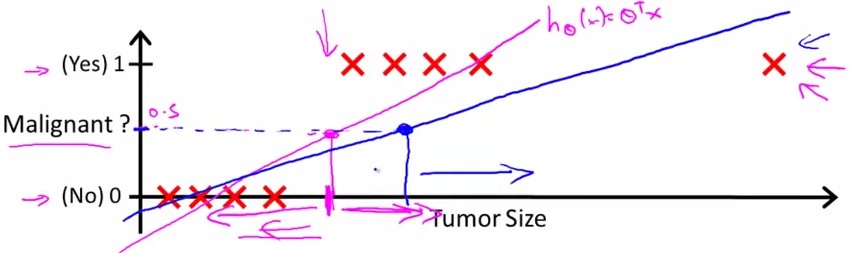
这种情况下，假设linear regression预测为蓝线，那么由0.5的boundary得到的线性方程中，不能很好地进行分类。因为不满足

y=1, h(x)>0.5

y=0, h(x)<=0.5

这时，我们引入logistic regression model：

所谓Sigmoid function或Logistic function就是这样一个函数g(z)见上图所示

当z>=0时，g(z)>=0.5；当z<0时，g(z)<0.5

由下图中公式知，给定了数据x和参数θ，y=0和y=1的概率和=1

/*****************************（三）、decision boundary**************************/

所谓Decision Boundary就是能够将所有数据点进行很好地分类的h(x)边界。

如下图所示，假设形如h(x)=g(θ0+θ1x1+θ2x2)的hypothesis参数θ=[-3,1,1]T, 则有

predict Y=1, if -3+x1+x2>=0

predict Y=0, if -3+x1+x2<0

刚好能够将图中所示数据集进行很好地分类

Another Example:

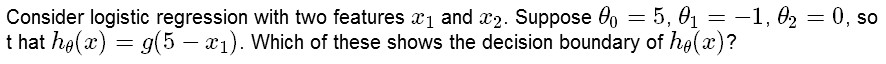
answer:

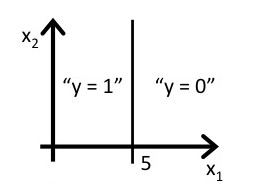
除了线性boundary还有非线性decision boundaries，比如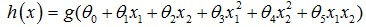

下图中，进行分类的decision boundary就是一个半径为1的圆，如图所示：

/********************（四）~（五）Simplified cost function and gradient descent<非常重要>*******************/

该部分讲述简化的logistic regression系统中how to implement gradient descents for logistic regression.

假设我们的数据点中y只会取0和1, 对于一个logistic regression model系统，有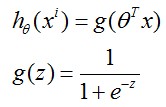，那么cost function定义如下：

由于y只会取0,1，那么就可以写成

不信的话可以把y=0,y=1分别代入，可以发现这个J（θ）和上面的Cost(hθ(x),y)是一样的(*^__^*) ，那么剩下的工作就是求能最小化 J(θ)的θ了~

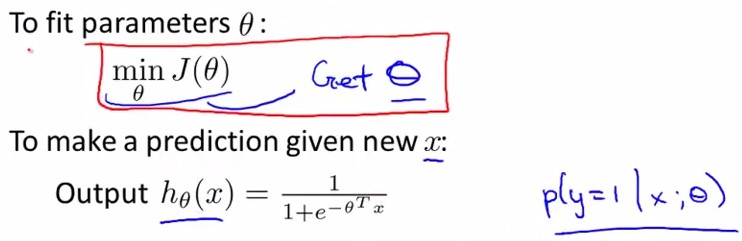
在第一章中我们已经讲了如何应用Gradient Descent, 也就是下图Repeat中的部分，将θ中所有维同时进行更新，而J(θ)的导数可以由下面的式子求得，结果如下图手写所示：

现在将其带入Repeat中：

这是我们惊奇的发现，它和第一章中我们得到的公式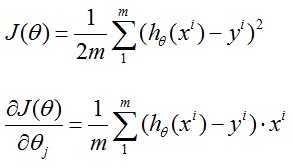是一样滴~

也就是说，下图中所示，不管h(x)的表达式是线性的还是logistic regression model, 都能得到如下的参数更新过程。

那么如何用vectorization来做呢？换言之，我们不要用for循环一个个更新θj，而用一个矩阵乘法同时更新整个θ。也就是解决下面这个问题：

上面的公式给出了参数矩阵θ的更新，那么下面再问个问题，第二讲中说了如何判断学习率α大小是否合适，那么在logistic regression系统中怎么评判呢？

Q：Suppose you are running gradient descent to fit a logistic regression model with parameter θ∈Rn+1. Which of the following is a reasonable way to make sure the learning rate α is set properly and that gradient descent is running correctly?

A：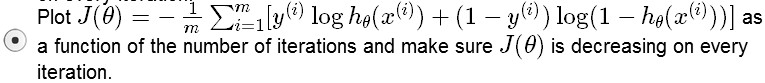

/*************（六）、Parameter Optimization in Matlab***********/

这部分内容将对logistic regression 做一些优化措施，使得能够更快地进行参数梯度下降。本段实现了matlab下用梯度方法计算最优参数的过程。

首先声明，除了gradient descent 方法之外，我们还有很多方法可以使用，如下图所示，左边是另外三种方法，右边是这三种方法共同的优缺点，无需选择学习率α，更快，但是更复杂。

也就是matlab中已经帮我们实现好了一些优化参数θ的方法，那么这里我们需要完成的事情只是写好cost function,并告诉系统，要用哪个方法进行最优化参数。比如我们用‘GradObj’， Use the GradObj option to specify that FUN also returns a second output argument G that is the partial derivatives of the function df/dX, at the point X.

如上图所示，给定了参数θ，我们需要给出cost Function. 其中，

jVal 是 cost function 的表示，比如设有两个点（1,0,5）和（0,1,5）进行回归，那么就设方程为hθ(x)=θ1x1+θ2x2;
则有costfunction J(θ)： jVal=(theta(1)-5)^2+(theta(2)-5)^2;

在每次迭代中，按照gradient descent的方法更新参数θ：θ(i)-=gradient(i),其中gradient(i)是J(θ)对θi求导的函数式，在此例中就有gradient(1)=2*(theta(1)-5), gradient(2)=2*(theta(2)-5)。如下面代码所示：

函数costFunction, 定义jVal=J(θ)和对两个θ的gradient：

function [ jVal,gradient ] = costFunction( theta )
%COSTFUNCTION Summary of this function goes here
%   Detailed explanation goes here

jVal= (theta(1)-5)^2+(theta(2)-5)^2;

gradient = zeros(2,1);
%code to compute derivative to theta
gradient(1) = 2 * (theta(1)-5);
gradient(2) = 2 * (theta(2)-5);

end

编写函数Gradient_descent，进行参数优化

function [optTheta,functionVal,exitFlag]=Gradient_descent( )
%GRADIENT_DESCENT Summary of this function goes here
%   Detailed explanation goes here

 options = optimset('GradObj','on','MaxIter',100);
 initialTheta = zeros(2,1)
 [optTheta,functionVal,exitFlag] = fminunc(@costFunction,initialTheta,options);

end

matlab主窗口中调用，得到优化厚的参数(θ1,θ2)=(5,5),即hθ(x)=θ1x1+θ2x2=5*x1+5*x2

 [optTheta,functionVal,exitFlag] = Gradient_descent()

initialTheta =

     0
     0


Local minimum found.

Optimization completed because the size of the gradient is less than
the default value of the function tolerance.

<stopping criteria details>


optTheta =

     5
     5


functionVal =

     0


exitFlag =

     1

最后得到的结果显示出优化参数optTheta=[5,5], functionVal = costFunction(迭代后) = 0

/*****************************（七）、Multi-class Classification One-vs-all**************************/

所谓one-vs-all method就是将binary分类的方法应用到多类分类中。

比如我想分成K类，那么就将其中一类作为positive，另（k-1）合起来作为negative，这样进行K个h(θ)的参数优化，每次得到的一个hθ(x)是指给定θ和x，它属于positive的类的概率。

按照上面这种方法，给定一个输入向量x，获得最大hθ(x)的类就是x所分到的类。

第二部分：The problem of overfitting and how to solve it

/************（八）、The problem of overfitting***********/

The Problem of overfitting:

overfitting就是过拟合，如下图中最右边的那幅图。对于以上讲述的两类（logistic regression和linear regression）都有overfitting的问题，下面分别用两幅图进行解释：

<Linear Regression>:

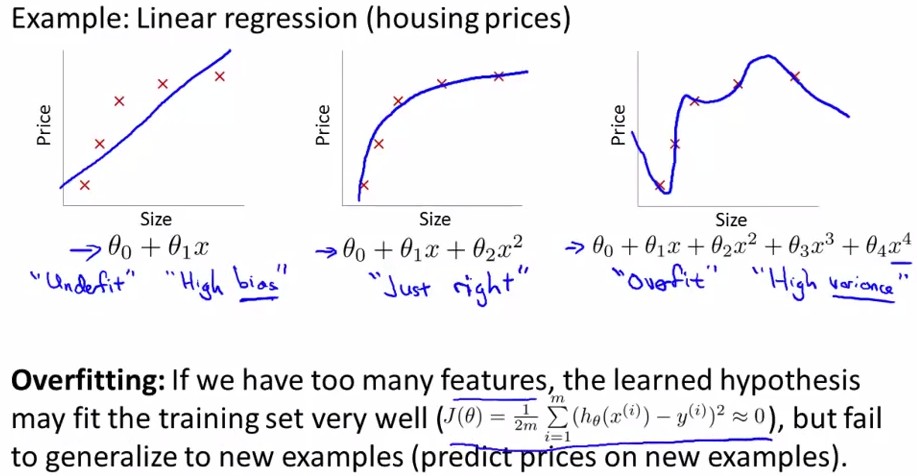
<logistic regression>:

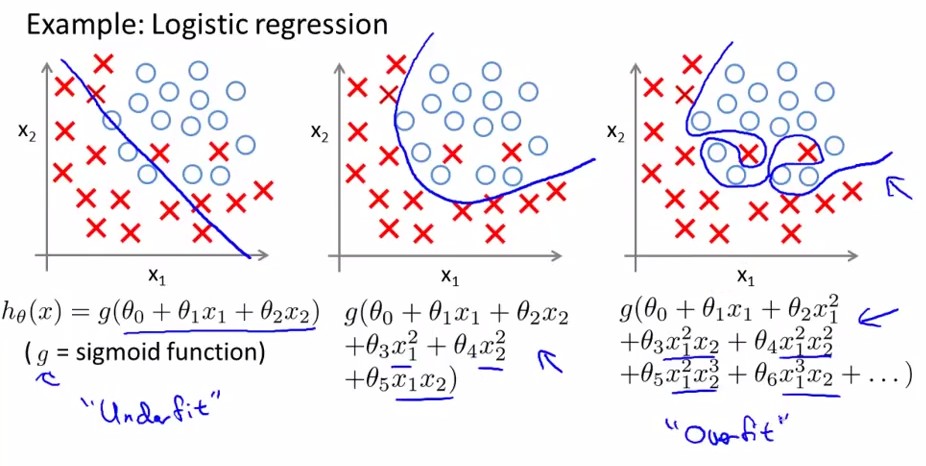
怎样解决过拟合问题呢？两个方法：

1. 减少feature个数（人工定义留多少个feature、算法选取这些feature）

2. 规格化（留下所有的feature，但对于部分feature定义其parameter非常小）

下面我们将对regularization进行详细的讲解。

对于linear regression model, 我们的问题是最小化

写作矩阵表示即

i.e. the loss function can be written as

there we can get:

After regularization, however,we have:

/************（九）、Cost Function***********/

对于Regularization，方法如下，定义cost function中θ3，θ4的parameter非常大，那么最小化cost function后就有非常小的θ3,θ4了。

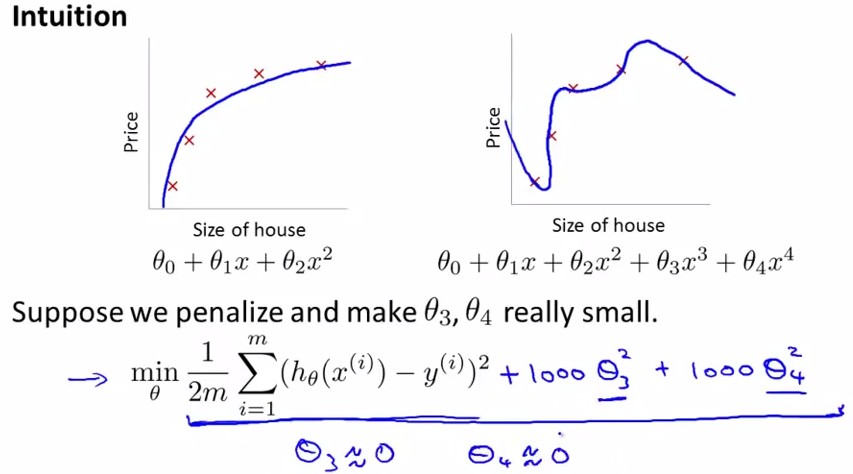
写作公式如下，在cost function中加入θ1~θn的惩罚项：

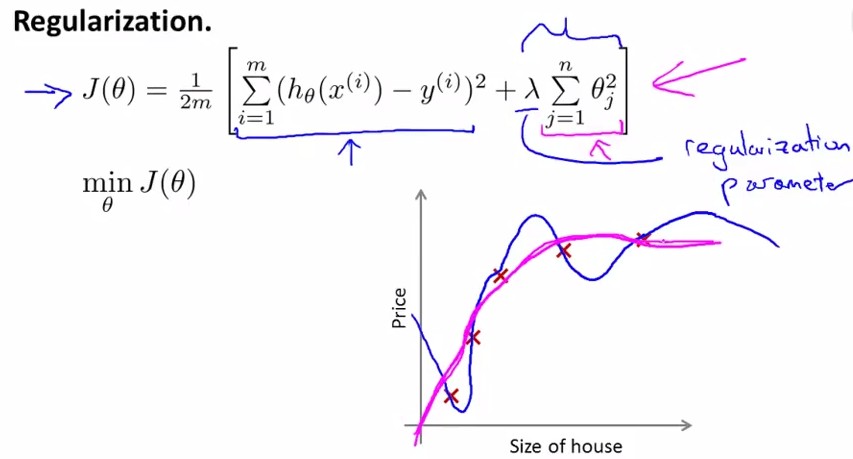
这里要注意λ的设置，见下面这个题目：

Q: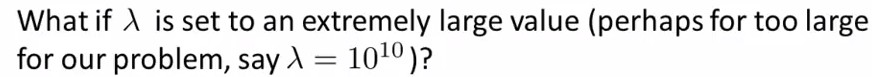

    A:λ很大会导致所有θ≈0

下面呢，我们分linear regression 和 logistic regression分别进行regularization步骤.

/************（十）、Regularized Linear Regression***********/

<Linear regression>:

首先看一下，按照上面的cost function的公式，如何应用gradient descent进行参数更新。

对于θ0，没有惩罚项，更新公式跟原来一样

对于其他θj，J(θ)对其求导后还要加上一项(λ/m)*θj，见下图：

如果不使用梯度下降法（gradient descent+regularization），而是用矩阵计算（normal equation）来求θ，也就求使J(θ)min的θ，令J(θ)对θj求导的所有导数等于0，有公式如下：

而且已经证明，上面公式中括号内的东西是可逆的。

/************（十一）、Regularized Logistic Regression***********/

<Logistic regression>:

前面已经讲过Logisitic Regression的cost function和overfitting的情况，如下图中所示:

和linear regression一样，我们给J(θ)加入关于θ的惩罚项来抑制过拟合：

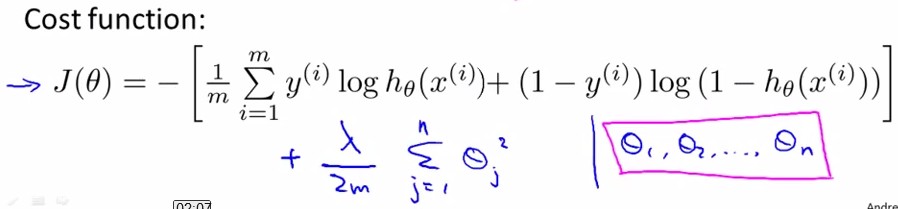
用Gradient Descent的方法，令J(θ)对θj求导都等于0，得到

这里我们发现，其实和线性回归的θ更新方法是一样的。

When using regularized logistic regression, which of these is the best way to monitor whether gradient descent is working correctly?

和上面matlab中调用那个例子相似，我们可以定义logistic regression的cost function如下所示：

图中，jval表示cost function 表达式，其中最后一项是参数θ的惩罚项；下面是对各θj求导的梯度，其中θ0没有在惩罚项中，因此gradient不变，θ1~θn分别多了一项(λ/m)*θj；

至此，regularization可以解决linear和logistic的overfitting regression问题了~