理解 CSS 中 transform matrix矩阵变换

一、概述

css中transform属性中的 translate、scale、rotate、skew变换属性均是通过matrix矩阵变换实现的。直接使用矩阵变换，实现位移、缩放、旋转、倾斜等动画，不够直观；实际开发中还是使用变换属性多一点。但这一点都不影响matrix属性的重要性；理解matrix属性定义的参数，需要一些线性代数的基础。

二、矩阵

1、矩阵的定义

将一些元素排列成若干行，每行放上相同数量的元素，就是一个矩阵。如：

 

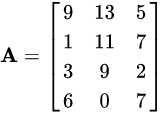
 2、矩阵的基本运算

加（减）法：

两个矩阵的加减法，取每个元素的对应的和（差）

 

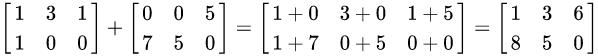
 数乘：

数字与矩阵元素之间的对应的乘积

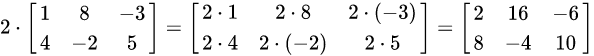
 矩阵乘法：

仅当第一个矩阵的列数(column)和第二个矩阵的行数(row)相等时才能定义。运算规则是，第一个矩阵行元素 与 第二个矩阵中的列元素，分别相乘求和，得到对应元素。例如 第一个矩阵的第一行元素[1 0 2]，与第二个矩阵的第一列元素[3,2,1],分别相乘求和，即：1 x 3 + 0 x 2 + 2 x 1 = 5；得到运算后矩阵的左上第一个元素。

 3、向量

物理学称为矢量，指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。

向量的分解：

直角坐标系中，任意向量可表示为：其中，i、j为单位向量。

 

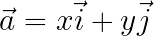
4、矩阵与向量

矩阵中的元素可以看做是一组坐标，而在平面直角坐标系中，一组向量可以使用坐标表示，因此可以使用矩阵表示一组向量，而对矩阵的运算，可以看做是对一组坐标的变换。来看具体的例子。

 三、矩阵变换

1、矩阵缩放

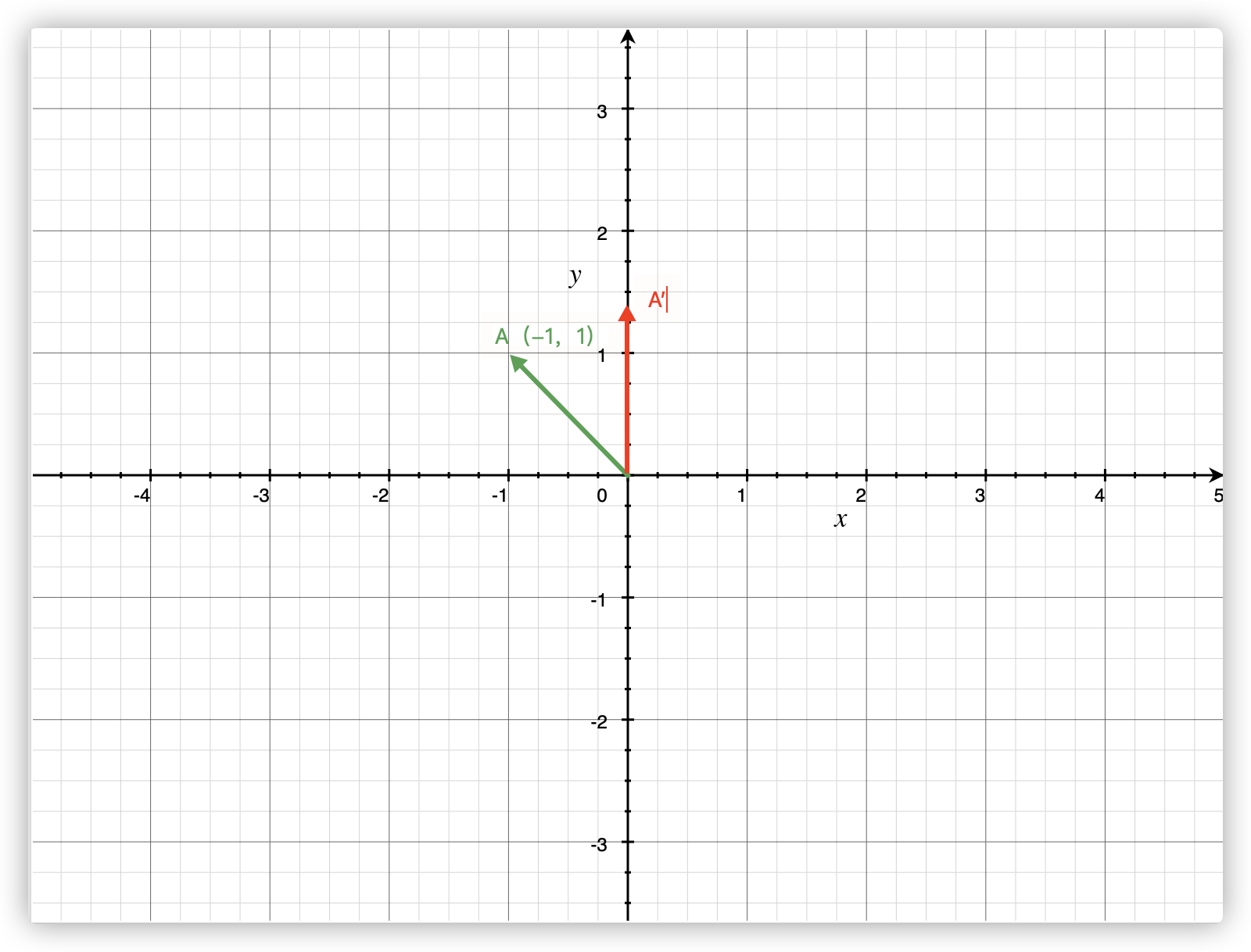
建立一个特殊的平面直角坐标系，坐标系中存在向量A(-1,1);考虑如何将其放大一倍。

 

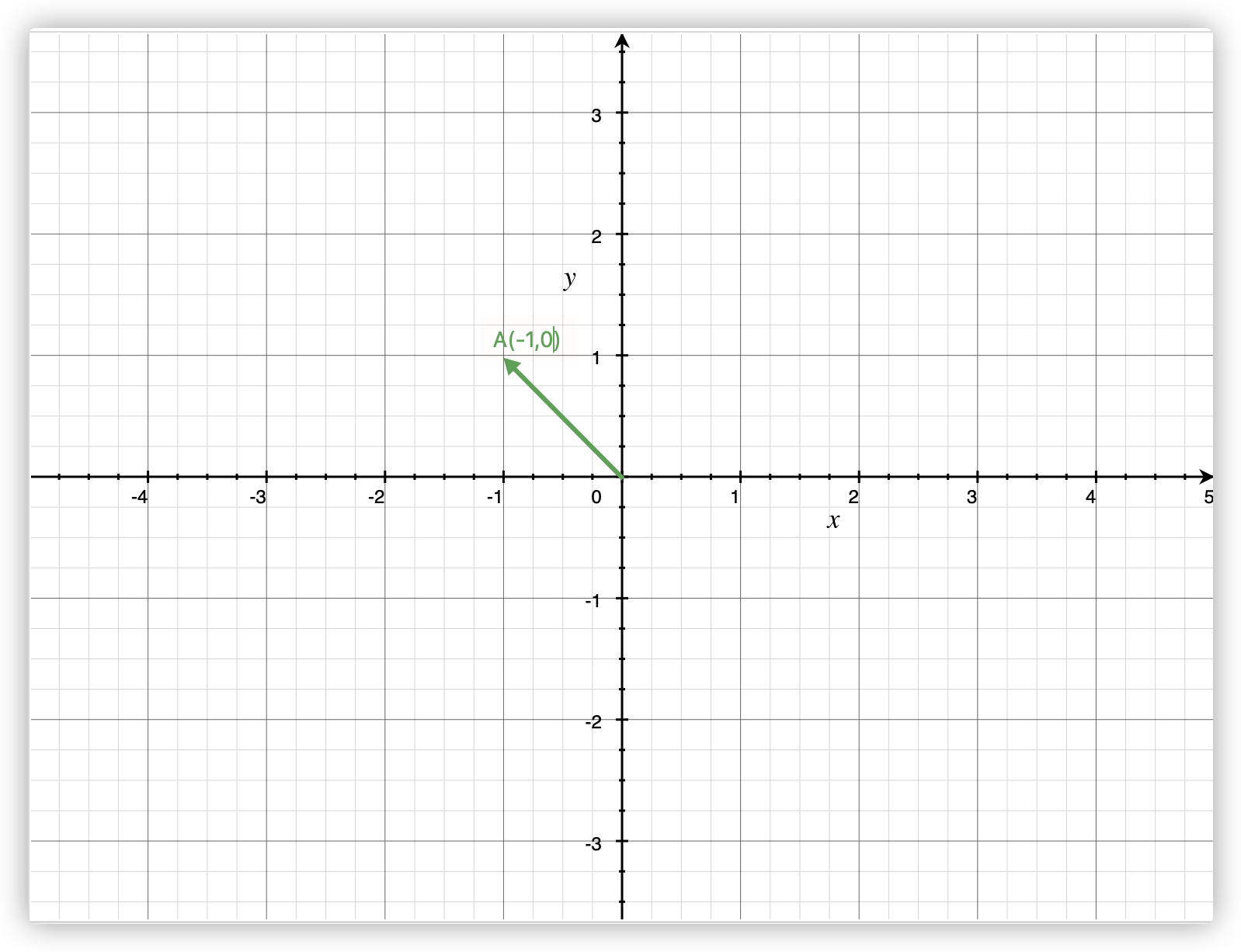
 我们变换基坐标系。根据公式有：

 

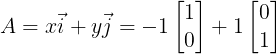
改变的是单位向量后，变换后的向量为：

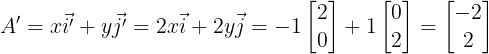
 2、矩阵的旋转

如何使坐标系中的向量发生旋转，考虑将向量A(-1,1),顺时针旋转45度。

 

 很显然需要旋转单位向量。有：

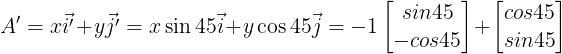
结果：

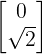
 对A向量旋转可以通过旋转单位向量实现，常见的变换操作，如缩放，旋转，倾斜，都可以通过变换单位向量实现。css matrix函数提供的参数就是描述一组单位向量的矩阵。

四、css中的矩阵变换

css 中 transform matrix 2d变换的参数一共有6个：

matrix(a, b, c, d, e, f)

其中默认参数为：

matrix(1, 0, 0, 1, 0, 0)

其中前4个参数，就是单位向量i(1,0)、j(0,1)。但注意，web页面中的坐标系原点在左上角，向右和向下对应平面直角坐标系的x轴和y轴正向；因此与平面直角坐标系的y轴的方向是相反的。

观察 transform 属性中的scale、rotate、skew是如何通过matrix矩阵来实现。

1、scale

使用scale缩放一个div的css是这样描述的：表示将宽和高同时放大两倍。

transform: scale(2); //同transform: scale(2,2)

使用矩阵达到上述效果，如果使用matrix实现，将单位向量放大两倍即可

transform: matrix(2,0,0,2,0,0);

 2、rotate

使用rotate顺时针旋转div 30deg：

transform: rotate(30deg);

使用matrix实现，只需旋转单位向量即可

transform: matrix(cosa, sina, -sina, cosa);

//transform: matrix(cos30°, sin30°, -sin30°, cos30°, 0, 0);

  //transform: matrix(0.866, 0.5, -0.5, 0.886 ,0 , 0);

3、skew

使用skew 倾斜30度：

transform: skew(30deg, 0);

使用matrix实现：

transform: matrix(1,tan(ay),tan(ax),1,0,0);  // matrix(1,0,0.5773502691896257,1,0,0);

 4、translate

上述3中变换均通过变换单位向量产生，原点都未发生变化。位移变化需要增加矩阵元素，和函数的参数，也是 matrix(a, b, c, d, e, f)中，e、f参数的作用，矩阵的形式可以变现为以下形式：

 如，坐标[-1,-1]，向右向上平移2个单位，得到变换后的坐标[1, 1]。

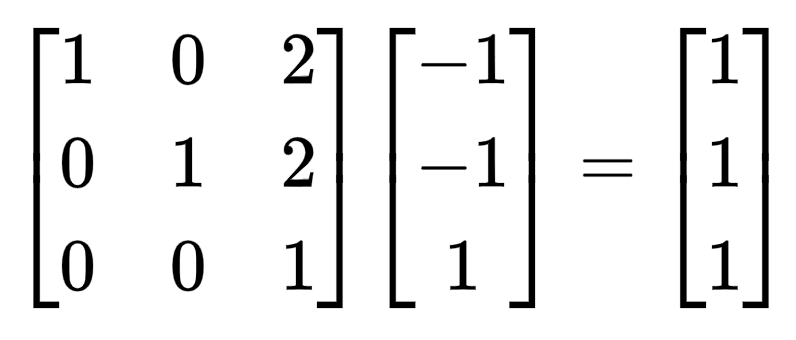
下面的css效果是一样的：

transform: translate(50px,0);
transform: matrix(1,0,0,1,50,0); 

使用matrix的形式，可以一次性定义上述4种变换。但使用transform， 需要将变换表达式写在一行,使用空格分隔有助于阅读，但不是必须的。

transform: skew(30deg,0) scale(2) rotate(30deg) translate(50px);

5、matrix3d 

matrix3d(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p)    //定义 3D 转换，使用 16 个值的 4x4 矩阵。

矩阵的形式为：

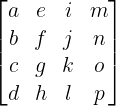
 6、2D变换的矩阵形式

给出一组transform变换（rotate、skew、translate、scale），将其转换成matrix函数的参数形式，需要注意以下几点：

1、rotate与skew变换是相互影响的，试图直接通过三角函数的计算得出相应的参数是不正确的，需要将其带入矩阵进行运算；

2、scale与translate变换理论上可以直接修改矩阵元素，也可以带入矩阵运算，但反复测试发现，translate带入矩阵后运算结果有误，这里直接修改矩阵元素。

3、矩阵运算比较复杂，使用的 Sylvester.js 库。以下是代码

function stringToMatrix(transformString) {
    try {
        // 参数检查
        if (typeof transformString !== 'string') {
            console.error('params must be string');
            return;
        }
        if (transformString.length === 0) {
            console.error('wrong transform format');
            return
        }
        if (['X', 'Y', '3d'].some(item => transformString.includes(item))) {
            console.error('3d transform unsupported yet');
            return;
        }
        let a = 1, b = 0, c = 0, d = 1, e = 0, f = 0;
        let reg = /(scale|rotate|skew|translate){1}\(.*?\)/g;
        let matrixDefault = $M([
            [1, 0, 0],
            [0, 1, 0],
            [0, 0, 1]
        ]);
        let matrixScale, matrixRotate, matrixSkew, matrixTranslate, matrixResult;
        transformString.match(reg).forEach(item => {
            let re = /\d+(.\d+)?/g;
            if (item.includes('rotate')) {
                let params = item.match(re);
                if (params) {
                    const i = params[0] / 180 * Math.PI;
                    matrixRotate = $M([
                        [Math.cos(i), -Math.sin(i), 0],
                        [Math.sin(i), Math.cos(i), 0],
                        [0, 0, 1]
                    ])
                    matrixResult = matrixResult ? matrixResult.x(matrixRotate) : matrixDefault.x(matrixRotate);
                }
            }
            if (item.includes('skew')) {
                let params = item.match(re);
                // to fix 角度不可超过90度
                const [i = 0, j = 0] = params.map(a => parseFloat(a));
                matrixSkew = $M([
                    [1, Math.tan(i / 180 * Math.PI), 0],
                    [Math.tan(j / 180 * Math.PI), 1, 0],
                    [0, 0, 1]
                ]);
                matrixResult = matrixResult ? matrixResult.x(matrixSkew) : matrixDefault.x(matrixSkew);
            }
            if (item.includes('scale')) {
                let params = item.match(re);
                let [i, j = i] = params.map(a => parseFloat(a));
                matrixScale = $M([
                    [i, 0, 0],
                    [0, j, 0],
                    [0, 0, 1]
                ]);
                matrixResult = matrixResult ? matrixResult.x(matrixScale) : matrixDefault.x(matrixScale);
            }
            if (item.includes('translate')) {
                let params = item.match(re);
                let [x = 0, y = 0] = params.map(a => parseFloat(a));
                e = x;
                f = y;
                matrixTranslate = $M([
                    [1, 0, x],
                    [0, 1, y],
                    [0, 0, 1]
                ]);
                if (matrixResult) {
                    matrixResult.elements[0][2] = x;
                    matrixResult.elements[1][2] = y;
                } else {
                    matrixDefault.elements[0][2] = x;
                    matrixDefault.elements[1][2] = y;
                }
            }
        })
        const [[a1, a2, a3], [b1, b2, b3], [c1, c2, c3]] = matrixResult.elements;
        return `matrix(${a1}, ${b1}, ${a2}, ${b2}, ${a3}, ${b3})`;
    } catch (error) {
        console.log(error)
    }
}

let transformString = 'skew(15deg) rotate(30deg) scale(1.5) translate(30px)';

stringToMatrix(transformString)// matrix(1.5, 0.7499999999999999, -0.401923788646684, 1.299038105676658, 30, 0)

 

参考连接：

1、https://zh.wikipedia.org/wiki/%E7%9F%A9%E9%98%B5#%E6%A0%87%E8%AE%B0

2、https://www.jianshu.com/p/dcf189998ae2