分类-MNIST(手写数字识别)
这是学习《Hands-On Machine Learning with Scikit-Learn and TensorFlow》的笔记,如果此笔记对该书有侵权内容,请联系我,将其删除。
这里面的内容目前条理还不是特别清析,后面有时间会更新整理一下。
下面的代码运行环境为jupyter + python3.6
获取数据
# from sklearn.datasets import fetch_mldata
# from sklearn import datasets
# mnist = fetch_mldata('MNIST original')
# mnist
好像下载不到它的数据,直接从网上找到它的数据,放到当面目录下的\datasets\mldata目录下。MNIST data的百度网盘链接: https://pan.baidu.com/s/1Np4r6uepYkPDHZsdMU4l-w 提取码: 9dq2,如果链接失效,可在下面评论区告知我,或者自己去网上找一样的,相信各位小伙伴的能力呀。
输入如下代码:
from sklearn.datasets import fetch_mldata
from sklearn import datasets
import numpy as np
mnist = fetch_mldata('mnist-original', data_home = './datasets/')
mnist
上面的代码中的data_home表示你的数据集的文件路径,写的是一个相对路径,如果你没有将你的数据集放在你当前代码的目录下,你可能需要使用绝对路径。
输出:
{'DESCR': 'mldata.org dataset: mnist-original',
'COL_NAMES': ['label', 'data'],
'target': array([0., 0., 0., ..., 9., 9., 9.]),
'data': array([[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
...,
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0]], dtype=uint8)}
可以看出,我们成功读到了它的数据,网上有很多的说法是错误的,没有办法读成功,只有这个才是正解😄。
上面的数据给出了一些基本的描述信息,里面有target, data,分别是标签和数据内容。进一步地我们可以看看数据和标签的维度信息。
输入如下代码:
X, y = mnist['data'], mnist['target']
print(X.shape)
print(y.shape)
输出:
(70000, 784)
(70000,)
从上面看出来,X是一个\(7000\times784\)的一个矩阵,一般来说,7000行表示有7000个样本,784列,表示样本有784这么多个属性。
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
some_digit = X[36000]
some_digit_image = some_digit.reshape(28,28)
plt.imshow(some_digit_image, cmap=matplotlib.cm.binary, interpolation="nearest")
plt.axis('off')
plt.show()

说个数看起来像是5,我觉得更像是6,我们可查看一下它的标签。
y[36000]
输出:
5.0
好吧,它的标签是5,可能这个标签写错了都不一定,我们得新写一下这个标签,说不定可以提高模型的准确率呢。这只是我个人在这里开玩笑说的,不用当真哈😉。
# EXTRA
def plot_digits(instances, images_per_row=10, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = matplotlib.cm.binary, **options)
plt.axis("off")
plt.figure(figsize=(9,9))
example_images = np.r_[X[:12000:600], X[13000:30600:600], X[30600:60000:590]]
plot_digits(example_images, images_per_row=10)
# save_fig("more_digits_plot")
plt.show()
输出如下图片:

在做数据的训练前,应该找出测试集,这里MNIST已经帮我们把测试集做好了。前面60000个当作训练集,后面10000个当测试集。
X_train, X_test, y_train, y_test = X[:60000],X[60000:],y[:60000],y[60000:]
MNIST的数据是按数字大小顺序排列的,所我们先要打乱它的顺序,这样可以保证我们的交叉验证是每一次都是相似的。
import numpy as np
shuffle_index = np.random.permutation(60000)
shuffle_index
输出:
array([52603, 56601, 42625, ..., 17778, 24267, 29358])
注: np.random.permutation 是随机排列一个序列。上面的例子就是从0~60000的随机序列
输入如下代码,打乱它的顺序。
X_train, y_train = X_train[shuffle_index],y_train[shuffle_index]
训练一个二分类器
先不做一个多类器,我们不去识别里面的手写数字是0~9中的某一个数。目前做一个最简单的,判断它是否是5,即将数据分成两个类别:“5”和“非5”
首先地,我们需要将标签更改一下,改成“是5”和“非5”的标签,很简单。
输出下面代码,形成一个了一个逻辑数组:
# 这是一个逻辑数组,5:True, 非5:False
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)
现在开始用一个分类器去训练它。用随机梯度下降分类器SGD。用Scikit-Learn的SGDClassifier类。这个分类器有一个好处是能够高效地处理非常大的数据集。部分原因是它每次只处理一条数据。
注: 我们暂时不用过多地在意
SGD是个什么样的分类器,只需要知道它是一个分类器就好啦😀
输入如下代码:
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state = 32)
sgd_clf.fit(X_train, y_train_5)
就这样子,我们训练好了一个分类器了,就是这么简单,实在是太容易了,也许你都还没有反应过来,就做了一件听起来这么牛逼的事情😎。
对上面的代码简单介绍一下,第3行,就是生成一个分类器,然后给一个random_state的参数,因为这个分类器有一定的随机性,所以它需一个随机种子。第4行,就是将我们的训练数据与我们的训练标签进行训练(拟合/回归)。
下面是它的输出:
SGDClassifier(alpha=0.0001, average=False, class_weight=None,
early_stopping=False, epsilon=0.1, eta0=0.0, fit_intercept=True,
l1_ratio=0.15, learning_rate='optimal', loss='hinge', max_iter=None,
n_iter=None, n_iter_no_change=5, n_jobs=None, penalty='l2',
power_t=0.5, random_state=32, shuffle=True, tol=None,
validation_fraction=0.1, verbose=0, warm_start=False)
接下来,我们用这个训练好的模型来预测一下,看看它到底怎么样。
输入如下代码:
sgd_clf.predict([some_digit])
输出:
array([ True])
这里面的some_digit是我前的数字5,不信可以翻到前面去看看。从输出的结果True可以看出来,这个模型预测正确了,确实是个5,看起来还不错。
这个模型的准确度你为似乎受随机种子的影响比较大,如果我将模型的随机种改为42,我们再来看一下它预测的结果是不是正确的
sgd_clf = SGDClassifier(random_state = 42)
sgd_clf.fit(X_train, y_train_5)
sgd_clf.predict([some_digit])
输出:
array([ True])
嗯,还是正确的,但是在你的电脑上,可能不一定,可以试试看。
对性能的评估
下面来整体评估一下这个分类的性能。上面我们只是让我们这个模型预测了一个数字,并不能代表什么,说不定是那个模型运气好,猜中了。我们接下来得整体看一下它的准确率,这样子才有说服力。
使用交叉验证测量准确性
交叉验证,简单来讲就是将我们的训练集又细分成好几份,比如说我们将它分成3份,使其中的2份来训练,1份用于测试,计算出它的准确率(或者其它指标)。这里每一份都需要用作测试,也需要被当作训练,所以要交叉3次,如果你对此还有所疑问,请百度或google一下。
在交叉验证过程中,有时候我们会需要更多的控制权,相较于函数cross_val_score()或者其他相似函数所提供的功能。下面代码做了和cross_val_score()相同的事情
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
skfolds = StratifiedKFold(n_splits = 3, random_state = 42)
clone_clf = clone(sgd_clf)
for train_index, test_index in skfolds.split(X_train, y_train_5):
X_train_folds = X_train[train_index]
y_train_folds = (y_train_5[train_index])
X_test_fold = X_train[test_index]
y_test_fold = (y_train_5[test_index])
clone_clf.fit(X_train_folds, y_train_folds)
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred == y_test_fold)
print(n_correct / len(y_pred))
注: StratfiedKFold 类实现了分层采样,生成的折包含了各类相应比例的样例。在每一次迭代,上述代码生成分类器的一个克隆,在克隆的模型上训练,在测试折上进行预测
输出:
0.9612
0.9531
0.9688
从上面的输出可以看出来,它的准确在95%以上,看起来还不错。
下面直接使用sklearn中的库进行交叉评估。使用cross_val_score函数来评估SGDClassifier模型。
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv = 3, scoring = "accuracy")
输出:
array([0.9612, 0.9531, 0.9688])
这精度看起来还不错,有大于95%的精度,有点让人兴奋,感觉做个分类还是挺容易的,一点都不难。但是不要高兴得太早。
我们再来看下一个非常简单的分类器去分类,看看它在“非5”这个类上的表现。
from sklearn.base import BaseEstimator
# 这个模型的预测的策略就是将所有的数据都认为是'非5'
class Never5Classifier(BaseEstimator):
def fit(self,X,y=None):
pass
def predict(self,X):
return np.zeros((len(X),1), dtype=bool)
这个分类器就是,不管青红皂白,都认为这个数字不是5,即将它归为非5。
never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv = 3, scoring = "accuracy")
输出:
array([0.90815, 0.9124 , 0.9084 ])
这么一个简单的分类器也有90%的精度😲,我们费了大半天劲,好像也只比这个准确率高那么一点点,有点掇败感。
这是因为只有10%的样本是5,其它都是非5,所以只我们一直猜这个图像不是5,当然有90%的精度,这叫数据不平衡。就像我们如果在日本,站到大街上,见到人就猜他是一个日本人,我们几乎肯定是正确的。
所以精度并不是一个好的性能度量指标,特别是在我们数据不平衡的时候。
混淆矩阵
对一般分类器来说,一人好得多的性能评估指标是混淆矩阵。大体思路是:输出类别A被分成类别B的次数。
为了计算混淆矩阵,首先你需要有一系列的预测值,这样才能将预测值与真实值做比较。你或许想在测试集上做预测。
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv = 3)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
array([[54306, 273],
[ 2065, 3356]], dtype=int64)
混淆矩阵中的每一行表示一个实际的类,而每一列表一个预测的类。该矩阵的第一行认为"非5"中的53993张被正确地归类为非5(这被称为真反例,true negatives),而其余586被错误归类为5(这被称为假正例,false positive),其余3905正确分类为"5"类(真正例,true positive)。一个完美的分类器将只有真反例和真正例,所混淆矩阵的非零值仅在其主对角线(左上至右下)。
# confusion_matrix(y_train_5, y_train_perfect_predictions)
混淆矩阵可以提供很多信息。有时候你会想要更加简明的指标。一个有趣的指标是正例预测的精度,也叫做分类器的准确率(precision)
其中\(TP\)是真正例的数目,\(FP\)是假正例的数目。
以准确率一般会伴随另一个指标一起使用,这个指标叫做召回率(recall),也叫做敏感度(sensitivity)或者真正例率(true positive rate, TPR)。这是正例被分类器正确探测出的比率。
\(FN\)是假反例的数目。
from sklearn.metrics import precision_score, recall_score
print(precision_score(y_train_5, y_train_pred))
print(recall_score(y_train_5, y_train_pred))
输出:
0.924772664645908
0.6190739715919572
这样看起,这个分类器的准确率并不高,只有56.8%左右,而且只是分成两类的一个分类器,这跟我们猜差不多。
通常结合准确率和召回率会更加方便,这个指标叫做F1值,特别是当你需要一个简单的方法去比较两个分类器的优劣的时时候。F1值是准确率和召回率的调和平均。
计算F1值,简单调用f1_score()即可。
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)
0.7416574585635358
F1支持那些有着相近准确率和召回率的分类(意思是只有当准确率和召回率一样大的时个,F1值才会大)。但并不是所的时候,我们都关心F1值,有时候我们只关心准确率(precision),或者有时候我们只关心召回率(recall)。
这里,我们再次理解一下准确率的含义:如果一个分类器的每次几乎都能把我们所要分的类别准确地分类出来,那么无疑,这个分类器的准确率是高的;什么时候准备率低呢,就是它把我们所要分的类,预测错了。比如我们这里的例子,我们要预测这张手写图片的数字是否是5,如果那张图真的是5,而我们的分类器预测它是5,那么它预测对了,当然预测对了,不是我们区分准确率与召回率的情况。如果将一张不是5的图片预测成5,那么我们会说它个分类器不是很准,它有低准确率。
什么是召回率?当我们将一张是5的图片预测成不是5,说明这个分类器还是比较严格的,那和它有较低的如回率。
总的来说,准确率低的原因就产将那些看起来像5(只是像,实际并不是5)的预测成了5;而召回率低的原因是把那些看起来不像5(实际上是5,只是可能那个5写得比较丑)预测成不是5。
在这里,我以自己的理解,举两个例子,比如公司想找个人当总经理,有一群人来应聘它。我们这时候的目标是,找到的这个人肯定是能够当总经理的,就算有的人看起来像是能当总经理,但是为了确保万无一失,我们要找一个看起来非常非常像能够当总经理的人。这个时候我们当然有着很高的准确率,因为我们找的人几乎肯定是能够当总经理的,但是此时,我们会犯另一个错误,就是有些人确实有能力当总经理,只是我们没有看出来(人不可貌像),所以我们拒绝他,因此我们有低的召回率,这在统计学上被称为犯了第一类错误,即弃真。这样做是合理的,因为即使弃真,但我们保真了。
另一种情况是,比如警察在一群人中想找出几个犯罪的人,这个时候我们就不能要超高的准确率了,因为有可能把真正的犯人放走。找犯人的原则一般是,只要他看起来像个犯人,都应该审查一下,即使最后真像大白后,他真的不是一个犯人。我们平时听到的宁可错杀一千,不可放走一个说的就是这个道理,因此这有着比较低的准确率,但是有高的召回率,这在统计学上被称为犯了第二类错误,即取伪。
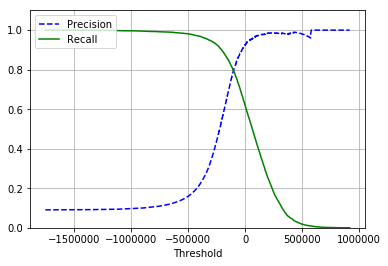
准备率/召回率之间的折中
y_scores = sgd_clf.decision_function([some_digit])
y_scores
输出:
array([15905.22111141])
threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
输出:
array([ True])
y_scores = cross_val_predict(sgd_clf, X_train,y_train_5,cv=3,
method = "decision_function")
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label = "Precision")
plt.plot(thresholds, recalls[:-1], "g-", label = "Recall")
plt.xlabel("Threshold")
plt.legend(loc="upper left")
plt.ylim([0,1.1])
plot_precision_recall_vs_threshold(precisions,recalls,thresholds)
plt.grid()
plt
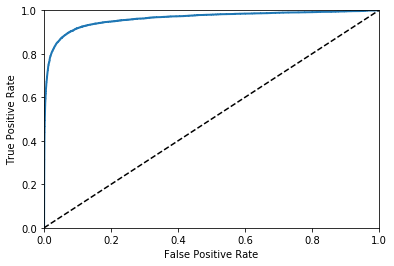
ROC曲线
受试者工作特征(ROC)曲线是另一个二分类器常用的工具。它非常类似与准确率/召回率曲线,但不是画出准确率对召回率的曲线,,ROC曲线是真正例率(true positive rate,另一个名字叫做召回率)对假正例率(false positive rate, FPR)的曲线。FPR是反例被错误分成正例的比率。它等于1减去真反例率(true negative rate,TNR)。TNR是反例被正确分类的比率。TNR也叫做特异性。
为了画出ROC曲线,你首先需要计算各种不同阈值下的TPR、FPR,使用roc_curve()函数:
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, label = None):
plt.plot(fpr,tpr, linewidth = 2, label = label)
plt.plot([0,1],[0,1],'k--')
plt.axis([0,1,0,1])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plot_roc_curve(fpr,tpr)
plt
一个比较分类器之间优劣的方法是:测量ROC曲线下的面积(AUC)。一个完美的分类器的 ROC AUC 等于1,而一个纯随机分类器的ROC AUC等于0.5。Scikit-Learn提供了一个函数来计算ROC AUC:
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5,y_scores)
0.9623990527630832
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state = 42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3, method = "predict_proba")
y_scores_forest = y_probas_forest[:,1]
fpr_forest, tpr_forest, thresholds_forest=roc_curve(y_train_5,y_scores_forest)
plt.plot(fpr,tpr,"b:",label="SGD")
plot_roc_curve(fpr_forest,tpr_forest,"Random Forest")
plt.legend(loc="bottom right")
plt
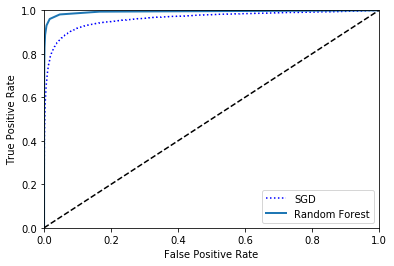
# 将概率大于0.5的,置为true, 否则为false
print(precision_score(y_train_5, y_scores_forest > 0.5))
print(recall_score(y_train_5, y_scores_forest > 0.5))
0.9844298245614035
0.8280760007378712
可以看出来,它的准确率还可,挺高的。
下面我们将分类出更多的数字,而不仅仅是5。
多类分类
二分类器只能分出两个类,而多分类器能分出多于两个类别的类。
一些算法(比如随机森林分类器或者朴素贝叶斯分类器)可以直接处理多类分类问题。其他一些算法(比如SVM分类器或者线性分类器)则是严格的二分类器,然后有许多策略可以让你用二分类器去执行多类分类。
Scikit-Learn可以探测出你想使用一个二分类器去完成多分类的任务,它会自动地执行OvA(除了SVM分类器,它使用OvO)。让我们试一下SGDClassifier
sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit])
array([5.])
你可以调用decision_function()方法。不是返回每个样例的一个数值,而是返回10个数值,一个数值对应于一个类。
some_digit_scores = sgd_clf.decision_function([some_digit])
some_digit_scores
array([[-253639.46707377, -425198.63904333, -354213.80127786,
-229676.13263264, -376404.48500382, 15905.22111141,
-564592.12430579, -194289.65607053, -748913.30208666,
-597652.52038338]])
最高的数值对应类别5
np.argmax(some_digit_scores)
5
sgd_clf.classes_
array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
如果你想强制Scikit-Learn使用OvO策略或者OvA策略,你可以使用OneVsOneClassifier类或者OneVsRestClassifier类。创建一个样例,传递一个二分类器给它的构造函数。举例子,下面的代码会创建一个多类分类器,使用OvO策略,基于SGDClassifier。
from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(random_state=42))
ovo_clf.fit(X_train, y_train)
ovo_clf.predict([some_digit])
array([5.])
训练一个RandomForestClassifier同样简单:
forest_clf.fit(X_train,y_train)
forest_clf.predict([some_digit])
array([5.])
这次Scikit-Learn没有必要去运行OvO或者OvA, 因为随机森林分类器能够直接将一个样例分到多个类别。你可调用predict_proba(),得到样例对应的类别的概率值的列表:
forest_clf.predict_proba([some_digit])
array([[0. , 0. , 0. , 0. , 0. , 0.9, 0. , 0. , 0.1, 0. ]])
接下来,我们当然想评估一下这些分类器。像以前一样,想便用交叉验证。让我们用cross_val_score来评估SGDClassifier的精度。
cross_val_score(sgd_clf, X_train, y_train,cv = 3, scoring = "accuracy")
array([0.86002799, 0.8760438 , 0.88093214])
我们可以看到这个分类器有86.3%的精度,这个精度还不错,比我们随便乱猜的精度要高出不少(如果我们随机猜,那么精度只有10%)。看起来也并不差,这里可以使输入正则化,得到更高的精度,可以将其精度提高到90%以上。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv = 3, scoring="accuracy")
array([0.9080184 , 0.91049552, 0.91043657])
误差分析
分析模型产生的误差,首先,我们可以检查混淆矩阵。需要使用cross_val_predict()做出预测,然后调用confusion_matrix()函数,像以前做的那样
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv = 3)
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx
array([[5739, 3, 22, 8, 9, 50, 43, 7, 38, 4],
[ 2, 6451, 50, 23, 6, 46, 5, 14, 133, 12],
[ 58, 38, 5348, 87, 76, 26, 83, 56, 169, 17],
[ 50, 40, 134, 5300, 2, 267, 37, 64, 140, 97],
[ 25, 26, 36, 7, 5356, 9, 54, 32, 83, 214],
[ 68, 37, 34, 179, 74, 4617, 106, 30, 171, 105],
[ 35, 21, 42, 2, 39, 98, 5630, 6, 44, 1],
[ 27, 18, 66, 27, 52, 10, 7, 5793, 17, 248],
[ 58, 150, 68, 140, 16, 156, 51, 29, 5050, 133],
[ 43, 29, 24, 84, 158, 36, 3, 194, 83, 5295]],
dtype=int64)
这里是一堆数字,使用Matplotlib的matshow()函数,将混淆矩阵以图像的方式呈现,将会更加方便。
plt.matshow(conf_mx, cmap = plt.cm.gray)
plt.show()

可以看到,几乎所有的图片都在对角线上,这意味着分类几乎全部正确。现我们只看看其误差的图像
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap = plt.cm.gray)
plt.show()
现在可以清楚看出分类器的各类误差,其中行代表实际类别,列代表预测的类别。第8、9列很亮,这说明很多图片被误分成数字8或者数字9。
分析混淆矩阵通常可以提供深刻的见解去改善分类器。回顾这幅图,看样子应该努力改善分类器在数字8和数字9上的表现,和纠正3/5的混淆。举例子,你可以尝试去收集更多的数据,或者你可以构造新的、有助于分类器的特征(新的分类器的特征,我们可以在数据里面加一个新的列———这相当添加了一个新的属性,比如字数8有两个环,数字6有一个,5没有)。
cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
# save_fig("error_analysis_digits_plot")
plt.show()

多标签分类
到目前为止,所有的样例都总是被分配到仅一个类(比如我们前面训练的分类,要么输出是1,要么是2,3,...,9,一次只能输出一个类别)。有些情况下,你也许想让你的分类器给一个样例输出多个类别。比如有时候我们想识别某个人脸,想判断它的性别,还有是否为中国人,这就有两个类别了([gender, isChinese])。。这种输出多个二值标签的分类系统被叫做多标签分类系统。
目前不打算深入脸部识别。我们可以先看一个简单点的例子。
from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >=7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform')
这段代码创造了一个y_multilabel数组,里面包含两个目标标签。第一个标签指出这个数字是否为大数(即是否为7,8,9),第二个标签指示这个数字是否为奇数
knn_clf.predict([some_digit])
array([[False, True]])
这个预测器预测对,我们输入的数据代表5,5不是一个大数,但是是一个奇数。
# y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_train, cv = 3)
# f1_score(y_train, y_train_knn_pred, average="macro")
多输出分类
我们即将讨论最后一种分类任务,被叫做"多输出-多分类"(或者简称多输出分类)。在这里每一个标签可以是多类别的(比如我们前面所举的例子)
为了说明这点,我们建立一个系统,它可以去除图片当中的噪音。它将一张混有噪音的图片作为输入,期待它输出一张干净的数字图片,用一个像素强度的数组表示,就像 MNIST图片那样。注意到这个分类器的输出是多标签的(一个像素一个标签)和每个标签可以有多个值 (像素强度取值范围从0到255)。所以它是一个多输出分类系统的例子。
我们从MNIST的图版创建训练集和测试集开始,然后给图片的像素强度添加噪声,这里是用NumPy的randint()函数。目标图像是原始图像。
noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = np.random.randint(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = matplotlib.cm.binary,
interpolation="nearest")
plt.axis("off")
some_index = 5500
plt.subplot(121); plot_digit(X_test_mod[some_index])
plt.subplot(122); plot_digit(y_test_mod[some_index])
# save_fig("noisy_digit_example_plot")
plt.show()
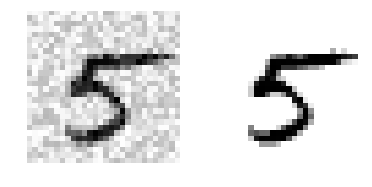
knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)
# save_fig("cleaned_digit_example_plot")
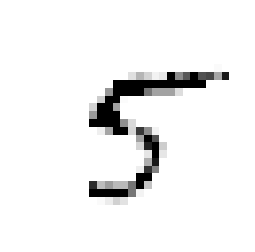
上面的图片看起来还行,比较接近原图片,去噪的效果还可以。
到这里,分类的知识学得差不多了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号