策树法(Decision Tree)
什么是决策树?
决策树(decision tree)一般都是自上而下的来生成的。每个决策或事件(即自然状态)都可能引出两个或多个事件,导致不同的结果,把这种决策分支画成图形很像一棵树的枝干,故称决策树。
决策树就是将决策过程各个阶段之间的结构绘制成一张箭线图,我们可以用下图来表示。
选择分割的方法有好几种,但是目的都是一致的:对目标类尝试进行最佳的分割。
从根到叶子节点都有一条路径,这条路径就是一条“规则”。
决策树可以是二叉的,也可以是多叉的。
对每个节点的衡量:
1) 通过该节点的记录数
2) 如果是叶子节点的话,分类的路径
3) 对叶子节点正确分类的比例
有些规则的效果可以比其他的一些规则要好。
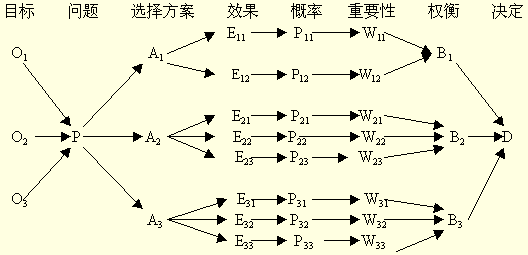
决策树的构成要素[1]
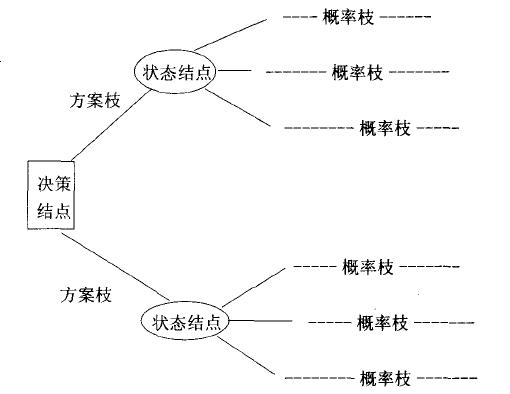
决策树的构成有四个要素:(1)决策结点;(2)方案枝;(3)状态结点;(4)概率枝。如图所示:
总之,决策树一般由方块结点、圆形结点、方案枝、概率枝等组成,方块结点称为决策结点,由结点引出若干条细支,每条细支代表一个方案, 称为方案枝;圆形结点称为状态结点,由状态结点引出若干条细支,表示不同的自然状态,称为概率枝。每条概率枝代表一种自然状态。在每条细枝上标明客观状态 的内容和其出现概率。在概率枝的最末稍标明该方案在该自然状态下所达到的结果(收益值或损失值)。这样树形图由左向右,由简到繁展开,组成一个树状网络图。
决策树对于常规统计方法的优缺点
优点:
1) 可以生成可以理解的规则;
2) 计算量相对来说不是很大;
3) 可以处理连续和种类字段;
4) 决策树可以清晰的显示哪些字段比较重要。
缺点:
1) 对连续性的字段比较难预测;
2) 对有时间顺序的数据,需要很多预处理的工作;
3) 当类别太多时,错误可能就会增加的比较快;
4) 一般的算法分类的时候,只是根据一个字段来分类。
决策树的适用范围[1]
科学的决策是现代管理者的一项重要职责。我们在企业管理实践中,常遇到的情景是:若干个可行性方案制订出来了,分析一下企业内、外部环境,大部分条件是己知的,但还存在一定的不确定因素。每个方案的执行都可能出现几种结果,各种结果的出现有一定的概率,企业决策存在着一定的胜算,也存在着一定的风险。这时,决策的标准只能是期望值。即,各种状态下的加权平均值。
针对上述问题,用决策树法来解决不失为一种好的选择。
决策树法作为一种决策技术,已被广泛地应用于企业的投资决策之中,它是随机决策模型中最常见、最普及的一种规策模式和方法此方法,有效地控制了决策带来的风险。所谓决策树法,就是运用树状图表示各决策的期望值,通过计算,最终优选出效益最大、成本最小的决策方法。决策树法属于风险型决策方法,不同于确定型决策方法,二者适用的条件也不同。应用决策树决策方法必须具备以下条件:
①具有决策者期望达到的明确目标;
②存在决策者可以选择的两个以上的可行备选方案;
⑧存在着决策者无法控制的两种以上的自然状态(如气候变化、市场行情、经济发展动向等);
④不同行动方案在不同自然状态下的收益值或损失值(简称损益值)可以计算出来;
⑤决策者能估计出不同的自然状态发生概率。
决策树的决策程序[1]
决策树法的决策程序如下:
(1)绘制树状图,根据已知条件排列出各个方案和每一方案的各种自然状态。
(2)将各状态概率及损益值标于概率枝上。
(3)计算各个方案期望值并将其标于该方案对应的状态结点上。
(4)进行剪枝,比较各个方案的期望值,并标于方案枝上,将期望值小的(即劣等方案剪掉)所剩的最后方案为最佳方案。
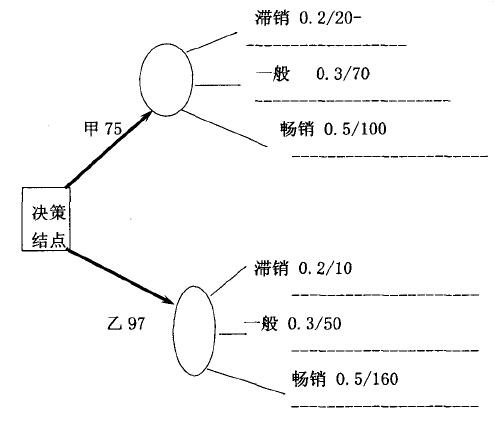
决策树法在企业决策中有着广泛的应用。下面举一实例说明其应用。某企业在下年度有甲、乙两种产品方案可供选择。每种方案都面I临滞销、一般、和畅销三种市场状态。各状态的概率和损益值如下:
-
市场状态
损益值方案滞销 一般 畅销 0.2 0.3 0.5 甲方案 20 70 100 乙方案 10 50 160
根据给出的条件运用决策树法选择一个最佳决策方案。
解题方法如下:
由此可以看出,决策树法的决策过程就是利用了概率论的原理,并且利用一种树形图作为分析工具。其基本原理是用决策点代表决策问题,用方案分枝代表可供选择的方案,用概率分枝代表方案可能出现的各种结果,经过对各种方案在各种结果条件下损益值的计算比较,为决策者提供决策依据。
决策树的应用前景[1]
从以上介绍可以看出决策树法具有许多优点:条理清晰,程序严严谨,定量、定性分析相结合,方法简单,易于掌握,应用性强,适用范围广等。人们逐渐认识到,在投资方案比较选择时考虑时间因素,建立时间可比原则和条件的重要性。当今的社会经济活动中,竞争日趋激烈,现代企业的经营方向面临着许多可供选择的方案,如何用最少的资源,赢得最大的利润以及最大限度地降低企业的经营风险,是企业决策者经常面对的决策问题,决策树法能简单明了地帮助企业决策层分析企业的经营风险和经营方向。必然地,随着经济的不断发展,企业需要做出决策的数量会不断地增加,而决策质量的提高取决于决策方法的科学化。企业的决策水平提高了,企业的管理水平就一定会提高。
西蒙说:管理就是决策。
决策树的应用举例
案例一:利用决策树评价生产方案
决策树是确定生产能力方案的一条简捷的途径。决策树不仅可以帮助人们理解问题,还可以帮助人们解决问题。决策树是一种通过图示罗列解题的有关步骤以及各步骤发生的条件与结果的一种方法。近年来出现的许多专门软件包可以用来建立和分析决策树,利用这些专门软件包,解决问题就变得更为简便了。
决策树由决策结点、机会结点与结点间的分枝连线组成。通常,人们用方框表示决策结点,用圆圈表示机会结点,从决策结点引出的分枝连线表示决策者可作出的选择,从机会结点引出的分枝连线表示机会结点所示事件发生的概率。
在利用决策树解题时,应从决策树末端起,从后向前,步步推进到决策树的始端。在向前推进的过程中,应在每一阶段计算事件发生的期望值。需特别注意:如果决策树所处理问题的计划期较长,计算时应考虑资金的时间价值。
计算完毕后,开始对决策树进行剪枝,在每个决策结点删去除了最高期望值以外的其他所有分枝,最后步步推进到第一个决策结点,这时就找到了问题的最佳方案。
下面以南方医院供应公司为例,看一看如何利用决策树作出合适的生产能力计划。
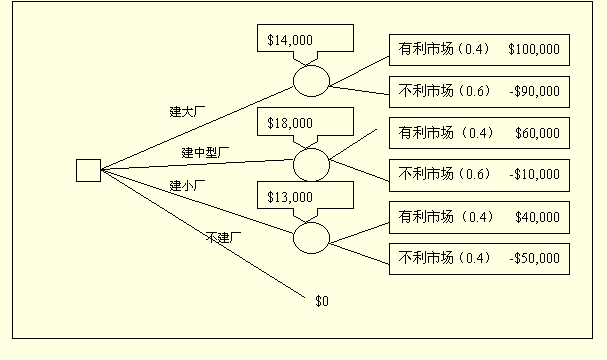
南方医院供应公司是一家制造医护人员的工装大褂的公司。该公司正在考虑扩大生产能力。它可以有以下几个选择:1、什么也不做;2、建一个小厂;3、建一个中型厂;4、建一个大厂。新增加的设备将生产一种新型的大褂,目前该产品的潜力或市场还是未知数。如果建一个大厂且市场较好就可实现$100,000的利润。如果市场不好则会导致$90,000的损失。但是,如果市场较好,建中型厂将会获得$ 60,000,小型厂将会获得$40,000,市场不好则建中型厂将会损失$10,000,小型厂将会损失$5,000。当然,还有一个选择就是什么也不干。最近的市场研究表明市场好的概率是0.4,也就是说市场不好的概率是0.6。参下图:
在这些数据的基础上,能产生最大的预期货币价值(EMV)的选择就可找到。
- EMV(建大厂)=(0.4)*($100,000)+(0.6)*(-$90,000)=-$14,000
- EMV(中型厂)=(0.4) *($ 600,000))+(0.6)* (-$10,000)=+$18,000
- EMV(建小厂)=(0.4)* ($40,000)+(0.6)*(-$5,000)=+$13,000
- EMV(不建厂)=$0
根据EMV标准,南方公司应该建一个中型厂。
案例二:决策树法在投标决策中的应用[2]
施工企业在同一时期内有多个工程项目可以参加投标,由于本企业资源条件有限,不可能将这些项目都承包下来,这类问题可用分析风险决策的决策树法来进行定量分析。
绘制方法
1.先画一个方框作为出发点,这个方框又称为决策点
2.从决策点向右引出若干根直线或折线每根直线或折线代表一个方案,这些直线或折线称为方案枝
3.每个方案枝的彩A画,个圆圈,这个圆圈称为概率分叉点,也称为自然状态点
4.从自然状态点引出若干根直线或折代表各自然状态的分枝这些直线或折线称为概率分枝
5.在概率分枝的AFaM标明各自然状态的损益值
决策树的分析最佳方案过程是比较各方案的损益值哪个方案的期望值最大则该方案为最佳方案
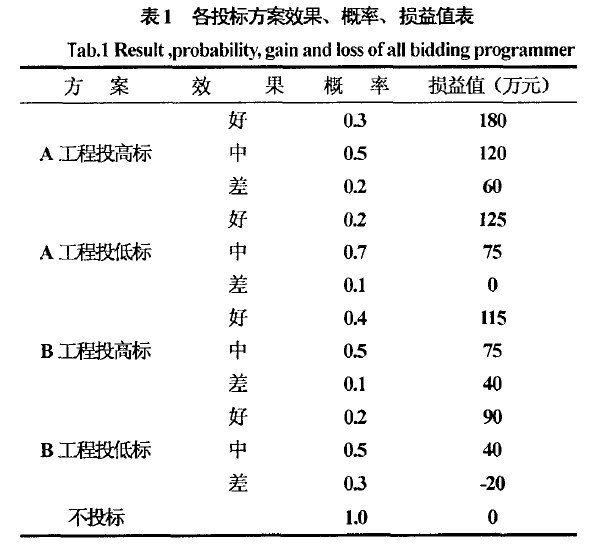
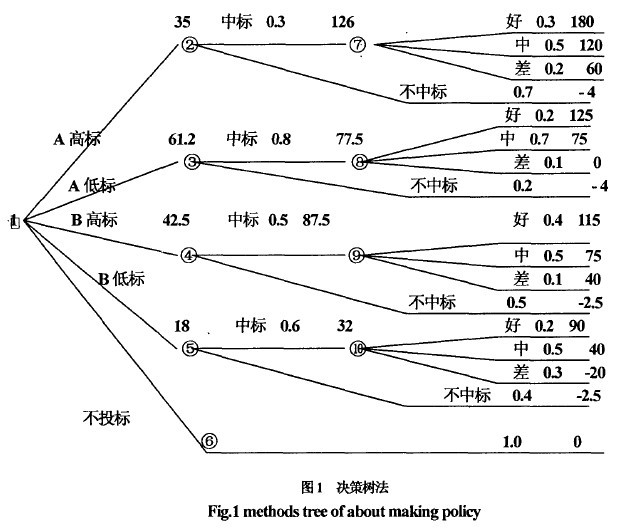
【例】某市属建筑公司面临A, B两项工程。因受本单位资源条件限制,只能选择其中一项工程投标或者这两项过程均不参加投标。根据过去类似工程投标的经验数据,A工程投高标的中标概率为0.3,投低标的中标概率为0.8,编制该工程投标文件的费用为4万元;B工程投高标的中标概率为0.5,投低标的中标概率为0.6,编制该工程投标文件的费用为2.5 万元各方案承包的效果、概率、损益值如表1所示
计算决策树上各机会点的期望值,并将计算出来的期望值标注在各机会点上方
机会点⑦: 180×0.3 + 120×0.5+ 60×0.2= 126
机会点②: 126×0.3 - 4×0.7=35
机会点⑧: 125×0.2+ 75×0.7 + 0×0.1=77.5
机会点③: 77.5×0.8- 4×0.2 = 61.2
机会点⑨: 115×0.4 + 75×0.5 + 40×0.1 = 87.5
机会点④: 87.5×0.5- 2.5×0.5 = 42.5
机会点⑩: 90×0.2 + 40×0.5 - 20×0.3 =32
机会点⑤: 32×0.6- 2.5×0.4=18
机会点⑥: 0
选择最佳方案
方案枝上机会点③的期望值(61.2)最大方案(A低标) 为最佳方案,该施工企业应对A工程投低标。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号