树结构是数据结构中非常重要的一种类型，本文将从最基础的普通树结构入门，延伸到二叉树，再延伸至二叉查找树。通过这种思路，让大家构建起关于树的最基本的知识链路。
普通树
树是一种非线性数据结构，它是数据元素按分支关系组织起来的结构，很像自然界中的树那样。
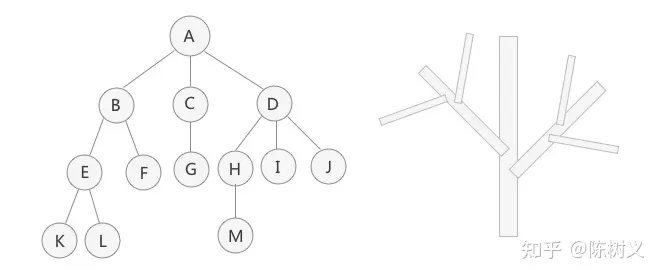
关于树的官方定义是：一棵树是由 N（N>0）个元素组成的有限集合，其中：
- 每个元素称为结点（node）。
- 有一个特定的结点，称为根结点或根（root）。
- 除根结点外，其余结点被分成 m（m>=0）个互不相交的有限集合，而每个子集又都是一棵树（称为原树的子树）。
关于树有几个重要的概念，这里简单做下介绍：
- 度
度即节点的分支数，例如上图树中节点 A 有三个子节点，那么我们称节点 A 的度是 3。
- 层次
节点的层次，表示节点在书中的位置。根结点的层次为 1，其他结点的层次等于它的父结点的层次数加 1。例如上图中节点 F 的层次为 3。
- 深度
树的深度，即组成该树各节点的最大层次。例如上图中节点的最大层次为 K/L/M，那么树的深度就为 K/L/M 任何一个的层次，即树的深度为 4。
- 路径
对于一棵子树中的任意两个不同的结点，如果从一个结点出发，按层次自上而下沿着一个个树枝能到达另一结点，称它们之间存在着一条路径。可用路径所经过的结点序列表示路径，路径的长度等于路径上的结点个数减 1。
例如上图中 A 到 L 的路径为：A > B > E > L，其路径结点个数为 4，那么其长度为 3。
二叉树
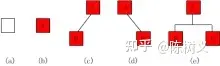
二叉树其实就是在普通树的基础上，加上了对树的度限制，即每个节点最多只能有两个子节点。 二叉树有五种基本的形态：
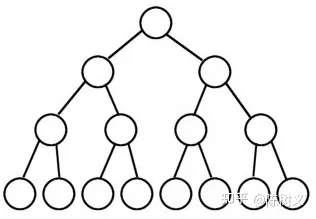
1、空二叉树 —— 如图 a 所示。 2、只有一个根结点的二叉树 —— 如图 b 所示。 3、只有左子树 —— 如图 c 所示。 4、只有右子树 —— 如图 d 所示。 5、完全二叉树 —— 如图 e 所示。
二叉树是一种简单且重要的树，许多其他类型的树都建立在二叉树的基础之上。根据叶子节点的不同情形，我们可以将二叉树再细分为：完满二叉树、完全二叉树、满二叉树。
完满二叉树，指的是所有非叶子节点的度都是 2（只有你有孩子，你必然有两个孩子）。
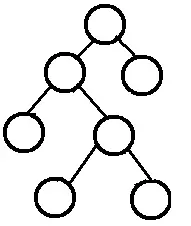
完全二叉树，指的是深度为 k，有 n 个结点的二叉树当且仅当其每一个结点都与深度为 k 的满二叉树中编号从 1 到 n 的结点一一对应。简单地说，完全二叉树是满二叉树的一个子集。简单地说，完全二叉树就是非叶子节点都有两个子节点，并且必须是从左到右、从上到下的顺序。
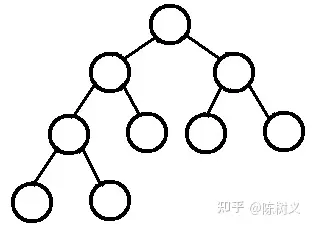
满二叉树，指的是一棵二叉树只有度为 0 的结点和度为 2 的结点，并且度为 0 的结点在同一层上，则这棵二叉树为满二叉树。 简单地说，就是所有叶子节点都在同一个层上，每一层都铺满了节点。
二叉查找树
上面学了那么多树结构的知识，但都没有实际应用，只能说是在打基础，了解基本概念。而二叉查找树可以说是一个非常实用的数据结构，可以用来快速查找元素。
二叉查找树（Binary Search Tree，BST），有些称其为二叉排序树，其平均查找效率为 O(logN)，最差查找效率为 O(N)（退化为链表）。而其能实现如此快速的查找速度，主要是其对于数据存储顺序的限制。
二叉查找树的定义为：
- 若左子树不空，则左子树上所有结点的值均小于它的根结点的值。
- 若右子树不空，则右子树上所有结点的值均大于它的根结点的值。
- 左、右子树也分别为二叉排序树
- 没有键值相等的结点
根据上面二叉查找树的定义，我们不难画出下面的二叉查找树。可以看到根节点的 7 元素，大于左边的 3 元素，小于右边的 11 元素。而左右子树 3、11 也同样符合这样的规律。
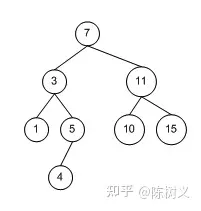
根据这样的元素排序，要查找一个元素最多只需要查找树的深度次数就够了。例如要查找元素 5，那么我们的查找路径是：7 > 3 > 5，只需要查找 3 次。而如果要查找 4，那么我们的查找路径是：7 > 3 > 5 > 4，只需要查找 4 次。根据二叉树的深度与节点数量的关系，我们就可以算出二叉查找树的深度为 O(LogN），即二叉查找树的时间复杂度为 O(LogN）。
二叉查找树在查询方面的效率提升是巨大的，比起链表来说提升了几万倍。特别是在数据量不断增大的情况下，其提升性能更加恐怖。例如我们有 1 亿个元素，如果使用链表存储，那么其平均需要比较 5000 万次。而使用二叉查找树存储，我们只需要比较 27 次就可以了。5000 万次与 27 次想比较，相差了 185 万倍！
但二叉查找树也有一个问题，即它在极端情况下会退化成链表。例如我们有这样一组数字：30、20、10、1，它们组成二叉查找树之后就会退化成普通链表。
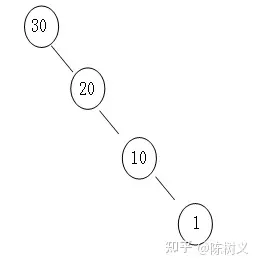
那么如何弥补二叉查找树的这个缺陷呢？这就涉及到了树的平衡这个概念。根据树平衡这个思路，先贤们又创造出了平衡二叉树这个概念，创造出了 AVL 树、红黑树等经典的数据结构。我们下回继续聊平衡二叉树。
总结
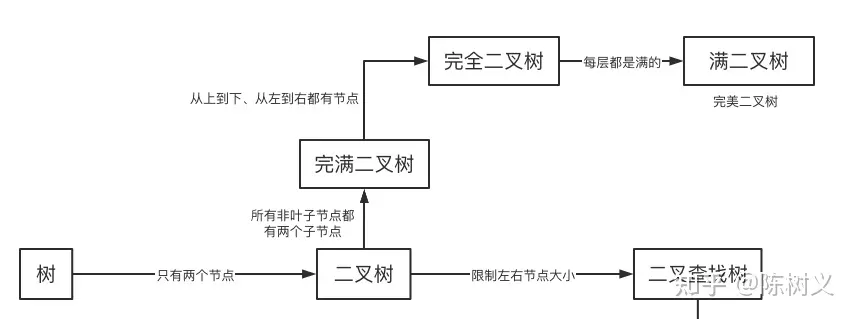
今天我们介绍了普通树结构，以及其相关的基础概念。接着我们介绍了非常基础的二叉树结构，接着将其扩展到完满二叉树、完全二叉树、满二叉树。最后，介绍了二叉查找树结构，以及存在的问题。从今天的文章中，我们可以得出一些结论：
- 二叉树是特殊的树结构，表示其最多只有两个节点。
- 完满二叉树是非叶子节点都有 2 个节点的二叉树。
- 完全二叉树是在完满二叉树的基础上，加上左右到有、从上到下都有节点的限制。
- 满二叉树是是在完全二叉树的基础上，加上每层的节点都是满的这个限制。
- 二叉查找树能实现 O（logN）的时间复杂度查找，但是会有退化成链表的风险。
到目前为止，我们将学习到的的树结构搭建起来，可以画出如下的树结构大道。
