时间序列异常检测zz

更新：

2022/04/07: 新增一些比较有用的github在useful link
2022/03/14: 新增统计异常检测方法 Grubbs' Test 和 ESD算法
2022/01/07: 新增振幅检测：异常检测_LaoChen_ZeroonE-CSDN博客_异常检测
2021/12/23: 新增孤立森林介绍iForest （Isolation Forest）孤立森林 异常检测 入门篇
2021/05/29：于4.2新增华为2020KPI异常检测算法大赛亚军解题思路
2021/05/24: Linkdin开源Greykite时间序列预测库
2021/03/18：推荐几本异常检测相关书籍，感觉作为入门书比较全面
《Outlier Analysis》—— Charu C. Agg
《Python深度学习异常检测》——清华大学出版社
2020/09/02：推荐一篇写的很好的关于视频监控异常检测的学报
监控视频异常检测：综述

一. 介绍

异常检测（Anomaly detection）是目前时序数据分析最成熟的应用之一，定义是从正常的时间序列中识别不正常的事件或行为的过程。有效的异常检测被广泛用于现实世界的很多领域，例如量化交易，网络安全检测、自动驾驶汽车和大型工业设备的日常维护。以在轨航天器为例，由于航天器昂贵且系统复杂，未能检测到危险可能会导致严重甚至无法弥补的损害。异常随时可能发展为严重故障，因此准确及时的异常检测可以提醒航天工程师今早采取措施。

  • 异常类型：
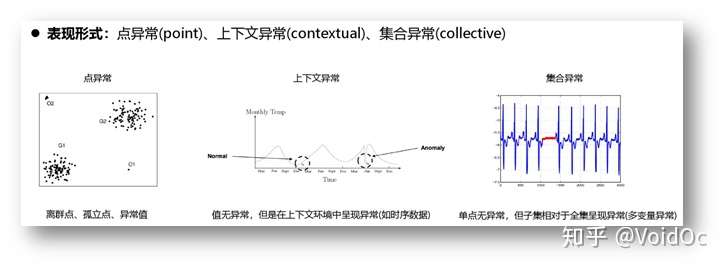
  • 异常检测方法：

1）直接检测：针对点异常，直接定位离群点，也称离群值检测。

2）间接检测：上下文或集合异常先转化成点异常，然后再求解。

3）时间跨度检测: ARIMA, 回归模型，LSTM等，核心思想就是模型学习一段历史数据，然后预测, 通过比对真实值与预测值的偏差来判断是否为异常。预测类算法在股市交易、量化金融领域有着广泛应用，有时间打算另开个坑。这里也推荐一本书：

《信用评价与股市预测模型研究及应用：统计学、神经网络与支持向量机方法》-- 庞素琳

4）序列跨度检测：许多传感器应用程序产生的时间序列通常彼此紧密相关。例如，在一个传感器上的鸟叫通常也会被附*的传感器记录下来。在这种情况下，经常可以使用一个序列来预测另一个序列。与此类预期预测的偏差可以报告为异常值，如隐式马尔科夫链HMM等。

二. 时间序列的特征工程

2.1 非数值型变量处理方法

（非数值型变量：categorical，text，mixed data）

极值分析和统计算法依赖于统计量化，例如均值或者标准差，对于非数值型变量，这些统计量化将不再有意义；但通过一些改变我们就能非数值型变量转化成数值型变量。

  • 分布概率转化：

就是变量不再默认服从特定分布（如高斯），而需要单独根据具体数据集定义概率分布（按比例），并按乘积方式与数 值变量组合以创建单个多元分布。

  • 线性转化：

1.One-hot码二进制转换，一个值对应一个种类，但容易维度爆炸，且无法体现不同类别的不同权重。可以通过将每列除以其标准偏差（deviation）来进行归一化。

2.潜在语义分析（Latent Semantic Analysis）

  • 基于相似度量的转化：

1.基于数据的统计邻域计算相似度，比如文本变量中“红色”和“橙色”比“红色”和“蓝色”更相*，但要求人为区分属性值之间的语义关系。

2.邻域相似度计算：

2.2 特征工程构造思路

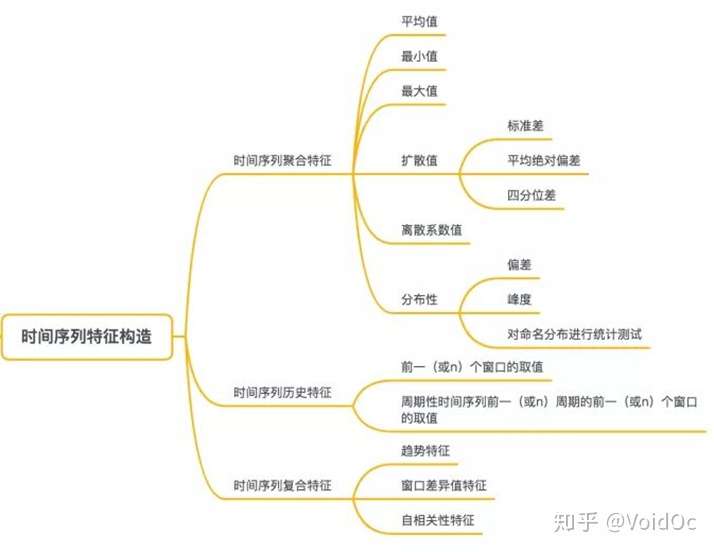常见的时间序列特征构造思路

1) 统计特征

  • max、min、interval
  • avg、median
  • variance、偏度、峰度

峰度（Kurtosis mesure）是一种用来衡量一列数据（单变量）离群度的特征量。第一步是计算均值μ和标准差σ， 并将数据标准化为0均值和单位1的方差：

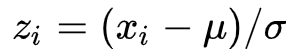
然后计算Zi四次幂的*均值，得到峰度如下：

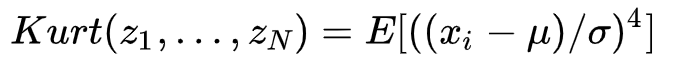
偏度和峰度如何影响您的分布 - Minitab​support.minitab.com/zh-cn/minitab/18/help-and-how-to/statistics/basic-statistics/supporting-topics/data-concepts/how-skewness-and-kurtosis-affect-your-distribution/
  • 同比、环比
  • 重复值

2) 拟合特征

  • 移动*均算法
  • 带权重的移动*均算法
  • 1/2/3次指数移动*均算法
  • SVD算法
  • 线性拟合
  • 自回归:AR/MA/ARMA/ARIMA/卡尔曼滤波器

3) 时域特征

  • 自相关，偏相关系数
  • 差分
  • 赫斯特指数
  • 趋势、周期
  • 噪声

4) 频域特征

  • 小波分析特征（大象流/老鼠流）：小波变换系数、变换波峰数、变换均值
  • 傅里叶变换偏度、峰度、方差、系数等

2.3 特征选择的方法

1）相关度（筛除无关特征）

相关度（Correlation）挑选的方法的基本的思想是：通常离群点是那些违反了正常数据依赖关系下模型的点，而无关的特征是不能用来单独建模的，反而会影响模型准确性。因此，我们首先可以通过回归模型利用其他特征来预测某一个特征，如果均方根误差RMSE很大，说明这个特征和其他特征相关度非常低，应该被剔除。

方法：将所有的特征标准化，然后分别利用其他的特征来预测第k（k=1…N）个特征，得到均方根误差RMSE_k = √(E((θ ̂-θ)^2 ))如果RMSE_k 大于1，则预测误差大于特征的方差，此时这个第k特征应当剔除。我们也可以用这种方法，通过给予权重来衡量特征的重要性。通常，第 k 特征的权重为max{ 0,1-RMSE_k }。

2）PCA 主成分分析：（筛除多重共线性特征）

去除*均值->计算协方差矩阵->计算协方差矩阵的特征值和特征向量->将特征值从大到小排序->保留最大的N个特征值以及它们的特征向量

3）树模型输出特征重要性排序（有监督场景）

作为单个决策树模型，在模型建立时实际上是寻找到某个特征合适的分割点。这个信息可以作为衡量所有特征重要性的一个指标。

基本思路如下：如果一个特征被选为分割点的次数越多，那么这个特征的重要性就越强。这个理念可以被推广到集成算法中，只要将每棵树的特征重要性进行简单的*均即可。

三. 时序异常检测算法

3.1 基于统计的算法（具有分布假设）

a) 针对单变量数据：

  • 集中不等式：集中不等式是数学中的一类不等式，描述了一个随机变量是否集中在某个取值附*
  • 马尔可夫不等式： 给出了一个实值随机变量取值大于等于某个特定数值的概率的上限。设X是一个随机变量，a>0为正实数，那么以下不等式成立：
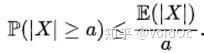
  • 比切雪夫不等式：马尔可夫不等式给出了随机变量处于区间 [a,+inf] 概率的上限估计。切比雪夫不等式则给出了随机变量集中在距离其数学期望值距离不超过a的区间上之概率的上限估计：
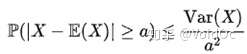
  • 统计置信度检验：
  • 3-sigma： (μ−3σ,μ+3σ)区间内的概率为99.74。所以可以认为，当数据分布区间超过这个区间时，即可认为是异常数据。
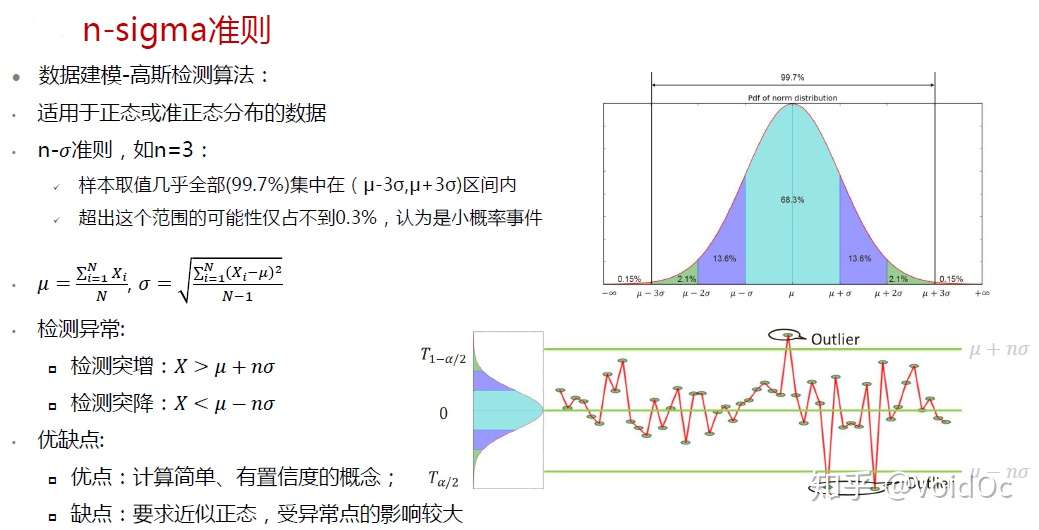n-sigma异常检测准则

预处理

-对于纯随机序列，也称为白噪声序列，序列的各项之间没有任何的关系， 序列在进行完全无序的随机波动， 可以终止对该序列的分析。

-对于*稳非白噪声序列， 它的均值和方差是常数。ARMA 模型是最常用的*稳序列拟合模型。

-对于非*稳序列， 由于它的方差和均值不稳定， 处理方法一般是将其转化成*稳序列。 可以使用ARIMA 模型进行分析。

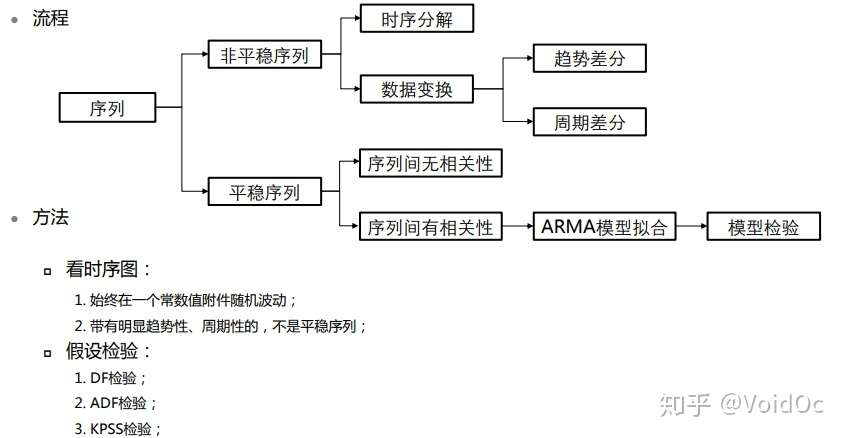预处理流程

建模

AR 是自回归， p 是自回归项， MA 是移动*均， q 为移动*均项， d 为时间序列称为*稳时 所做的差分次数。

原理： 将非*稳时间序列转换成*稳时间序列， 然后将因变量仅对它的滞后值（p阶）以及随机误差项的现值和滞后值进行回顾所建立的模型。

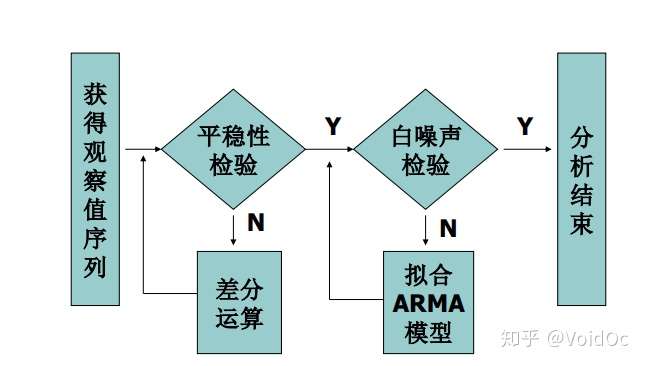
  • 实例：使用ARIMA 模型对某餐厅的销售数据进行预测
#coding=gbk
#使用ARIMA 模型对非*稳时间序列记性建模操作
#差分运算具有强大的确定性的信息提取能力， 许多非*稳的序列差分后显示出*稳序列的性质， 这是称这个非*稳序列为差分*稳序列。 
#对差分*稳序列可以还是要ARMA 模型进行拟合， ARIMA 模型的实质就是差分预算与 ARMA 模型的结合。 
 
#导入数据
import pandas as pd
filename = r'D:\datasets\arima_data.xls'
data = pd.read_excel(filename, index_col = u'日期')
 
#画出时序图
import matplotlib.pyplot as plt     
plt.rcParams['font.sans-serif'] = ['SimHei']    #定义使其正常显示中文字体黑体
plt.rcParams['axes.unicode_minus'] = False      #用来正常显示表示负号
# data.plot()
# plt.show()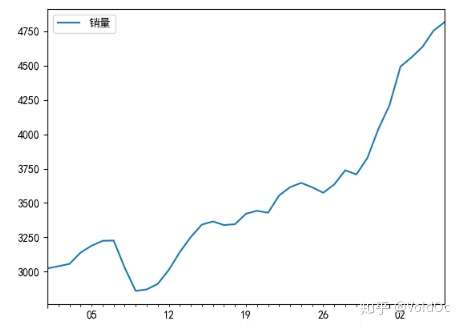
#画出自相关性图
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# plot_acf(data)
# plt.show()
 
#*稳性检测
from statsmodels.tsa.stattools import adfuller
print('原始序列的检验结果为：',adfuller(data[u'销量']))
#原始序列的检验结果为： (1.8137710150945268, 0.9983759421514264, 10, 26, {'1%': -3.7112123008648155,
#  '10%': -2.6300945562130176, '5%': -2.981246804733728}, 299.46989866024177)
#返回值依次为：adf, pvalue p值， usedlag, nobs, critical values临界值 , icbest, regresults, resstore 
#adf 分别大于3中不同检验水*的3个临界值，单位检测统计量对应的p 值显著大于 0.05 ， 说明序列可以判定为 非*稳序列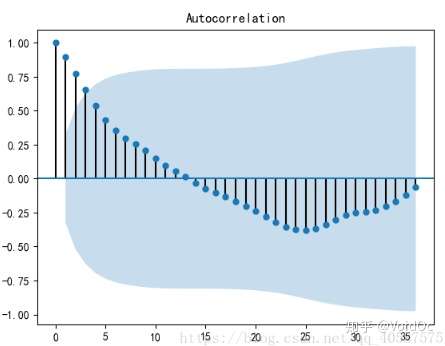
#对数据进行差分后得到 自相关图和 偏相关图
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
 
D_data.plot()   #画出差分后的时序图
# plt.show()
 
plot_acf(D_data)    #画出自相关图
# plt.show()
plot_pacf(D_data)   #画出偏相关图
# plt.show()
print(u'差分序列的ADF 检验结果为： ', adfuller(D_data[u'销量差分']))   #*稳性检验
#差分序列的ADF 检验结果为：  (-3.1560562366723537, 0.022673435440048798, 0, 35, {'1%': -3.6327426647230316, 
# '10%': -2.6130173469387756, '5%': -2.9485102040816327}, 287.5909090780334)
#一阶差分后的序列的时序图在均值附*比较*稳的波动， 自相关性有很强的短期相关性， 单位根检验 p值小于 0.05 ，所以说一阶差分后的序列是*稳序列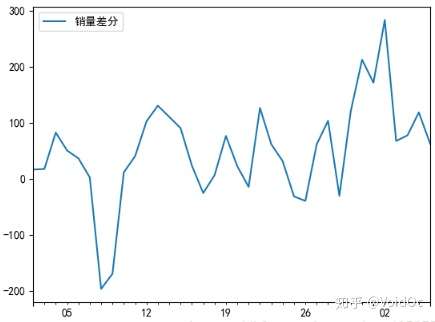
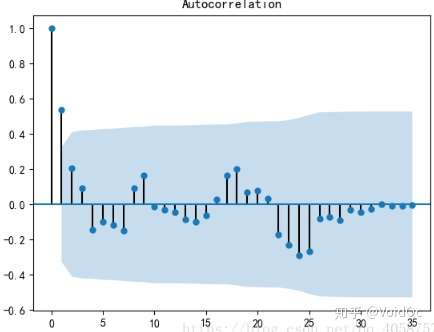
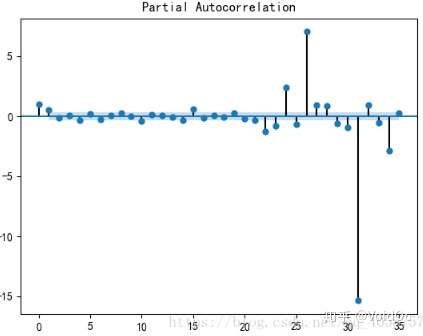
#对一阶差分后的序列做白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果：',acorr_ljungbox(D_data, lags= 1)) #返回统计量和 p 值
# 差分序列的白噪声检验结果： (array([11.30402222]), array([0.00077339])) p值为第二项， 远小于 0.05
 
#对模型进行定阶
from statsmodels.tsa.arima_model import ARIMA 
pmax = int(len(D_data) / 10)    #一般阶数不超过 length /10
qmax = int(len(D_data) / 10)
bic_matrix = []
for p in range(pmax +1):
    temp= []
    for q in range(qmax+1):
        try:
            temp.append(ARIMA(data, (p, 1, q)).fit().bic)
        except:
            temp.append(None)
        bic_matrix.append(temp)
 
bic_matrix = pd.DataFrame(bic_matrix)   #将其转换成Dataframe 数据结构
p,q = bic_matrix.stack().idxmin()   #先使用stack 展*， 然后使用 idxmin 找出最小值的位置
print(u'BIC 最小的p值 和 q 值：%s,%s' %(p,q))  #  BIC 最小的p值 和 q 值：0,1
#所以可以建立ARIMA 模型，ARIMA(0,1,1)
model = ARIMA(data, (p,1,q)).fit()
model.summary2()        #生成一份模型报告
model.forecast(5)   #为未来5天进行预测，返回预测结果、标准误差和置信区间

利用模型向前预测的时期越长， 预测的误差就会越大，这是时间预测的典型特点

 

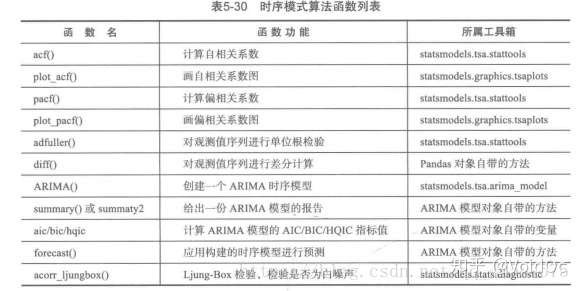
b) 针对多变量数据：

  • 马氏距离：用来计算样本X与中心点μ的距离，也可以用来做异常分值，计算方式:

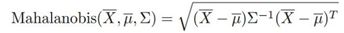
马氏距离最强大的地方是引入了数据之间的相关性（协方差矩阵）。 而且马氏距离不需要任何参数，这对无监督学习来说无疑是一件很好的方法。通常一个简单的最*邻算法加上马氏距离就可以秒杀很多复杂的检测模型。

（马氏距离+ KNN） DaiDongyang/knn

3.2 基于相似度量的算法

a) 基于距离度量

  • KNN

输入数据集D,参数k,n->对于每个点计算它的k邻*距离->按照距离降序排序->前N个点认为是离群点

b) 基于密度度量

  • LOF（Local Outlier Factor）：局部离群因子检测方法，该算法会给数据集中的每个点计算一个离群因子

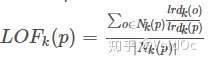
通过判断LOF是否接*于1来判定是否是离群因子。若LOF远大于1，则认为是离群因子，接*于1，则是正常点。

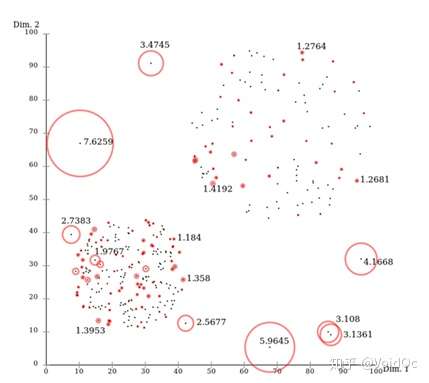LOF离群因子分布图

 

（LOF计算方法）：刘腾飞：机器学习-异常检测算法（二）：Local Outlier Factor

  • KDE 核密度估计：所谓核密度估计，就是采用*滑的峰值函数(“核”)来拟合观察到的数据点，从而对真实的概率分布曲线进行模拟：

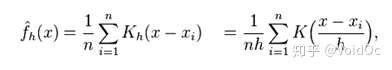
核密度函数的原理也比较简单，“核”是一个函数，用来提供权重。例如高斯函数 (Gaussian) 就是一个常用的核函数，如果某一个数在观察中出现了，我们可以认为这个数的概率密度很大，和这个数比较*的数的概率密度也会比较大，而那些离这个数远的数的概率密度会比较小。

（KDE计算方法）非参数估计：核密度估计KDE_皮皮blog-CSDN博客_python kde

c) 基于聚类：K-means，GMM

缺点：聚类参数难界定，导致检测效果偏差；聚类训练开销较大

d) 基于树：孤立森林（Isolation Forest）

iForest （Isolation Forest）孤立森林 异常检测 入门篇

基于集成学习（Ensemble），适用于连续数据的异常检测，通过多颗iTree形成森林来判定是否有异常点；这种方法很有效，但是并不总是有用的，比如说数据的分布不是沿着特征轴，而是随意分布，或者流型分布，就需要选择别的方式了。

iTree伪代码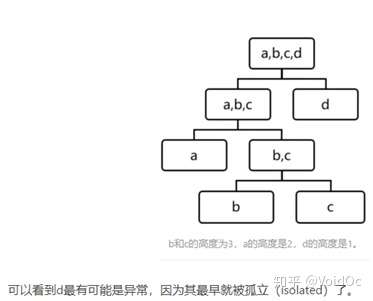IF模型结构示意图

f) 基于谱（线性模型）：通过与正常谱型进行残差对比，发现异常

简单的线性模型就是相关性分析。利用一些自变量来预测因变量。比较重要的一个应用就是时序数据或者空间轨迹数据。我们可以利用上一个值或者上几个值来预测当前值，将预测值和实际值的误差作为优化对象，这样就建立了一个正常数据的模型，背离这个模型的就被当作异常值，预测值和实际值的误差也可以作为异常分值来提供

  • One-class SVM 矩阵分解法:

（无监督，解决极度不*衡数据）

严格地讲，OneClassSVM不是一种异常点检测方法，而是一种奇异值检测方法，因为它的训练集不应该掺杂异常点（训练集只有一类），否则的话，可能在训练时影响边界的选取。 但在数据维度很高，或者对相关数据分布没有任何假设的情况下，OneClassSVM也可以作为一种很好的outlier detection方法。

  • Replicator Neural Networks and Deep Autoencoders：

基于神经网络（需要构造必要特征）适用于连续数据的异常检测，并通过寻找神经网络的重构误差来区分正常点和异常点。

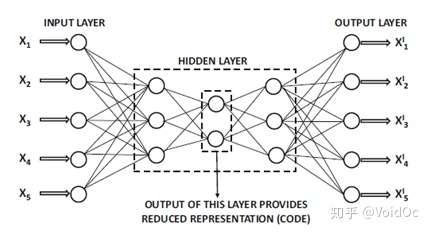
接着，我们可以通过训练样本库中人工标注的数据得到多种有监督模型，比如

逻辑回归/线性回归/决策树/RF/BGDT

四、深度学习方法

4.1 介绍

基于深度学习的时间序列异常检测算法，主要可以分为以下这么几种

a) 针对正常数据进行训练建模，然后通过高重构误差来识别异常点，即生成式（Generative）的算法，往往是无监督的，如自编码器（Auto Encoder）类 或者回声状态网络（Echo State Networks）。

b) 对数据的概率分布进行建模，然后根据样本点与极低概率的关联性来识别异常点，如DAGMM[1]。

c) 通过标注数据，告诉模型正常数据点长什么样，异常数据点长什么样，然后通过有监督算法训练分类模型，也称判别式（Discriminative）算法。

在判别式里面，包括时间序列的特征工程和各种有监督算法，还有端到端的深度学习方法。在端到端的深度学习方法里面，包括前馈神经网络，卷积神经网络，或者其余混合模型等常见算法。借用张大大的图大致做一个总结：

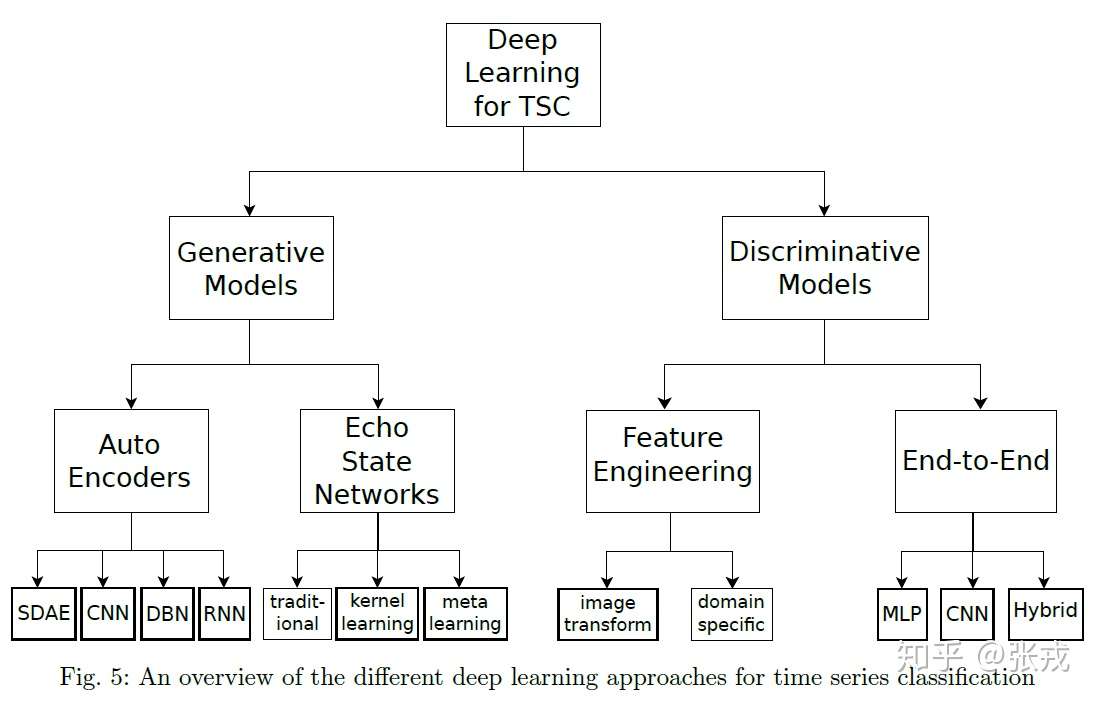
4.2 几种深度学习方法 + 代码实例

1） 基于AutoEncoder的无监督异常检测算法（Tensorflow）

有关AE算法的详解可以参考我的另一篇学习笔记，写得很详细，包括自编码器的变种与几类应用。
VoidOc：【深度学习】 自编码器（AutoEncoder）112 赞同 · 15 评论文章

2）Deep SVDD：来自论文Deep One-Class Classification[2]

一句话概括它的思想：使用一个神经网络将样本从输入空间 [公式] 映射到输出空间

[公式] 使得在隐空间上, 正常样本聚集类中心c附*。在测试时, 如果一个样本距离正常类中心c太远, 就认定为异常。如下图所示：

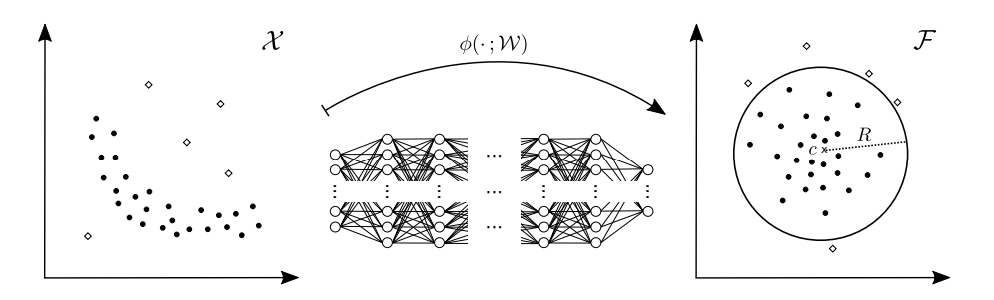
Deep SVDD这个方法是无监督的异常检测方法，充分利用标签信息之后， 我就可以让网络更加明确地区分正常样本和异常样本。理想的情况是想将正常样本和异常样本在输出空间聚成两簇， 如下图：

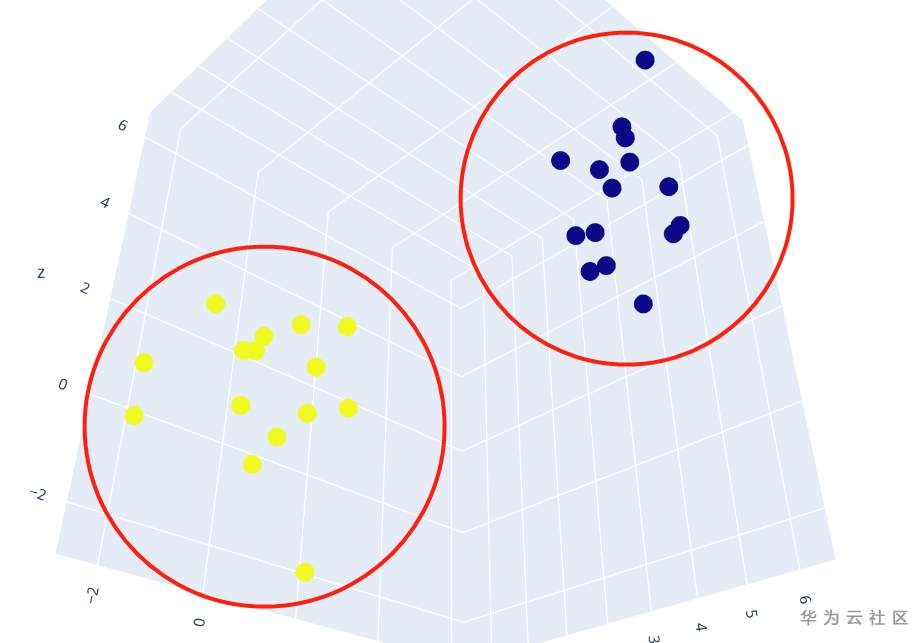
详细步骤如下：

构建一个简单的神经网络：

encoder = nn.Sequential(
    nn.Linear(input_size, 128),
    nn.ReLU(inplace=True),
    nn.Linear(128, 64),
    nn.ReLU(inplace=True),
    nn.Linear(64, output_size))

在这个网络中， 设置output_size = 3。这样的设定，一定程度上是为了方便在3维空间中将这些点画出来。所有的正常样本记为Xnor，所有的异常样本Xano，使用上述神经网络 [公式] 分别将他们映射到输出空间：

[公式]

[公式]

为了实现上图聚成两簇的效果，设计损失函数如下：

def loss(z_nor, z_ano):
# 计算两个类簇的中心
nor_center = torch.mean(z_nor, dim=0)
ano_center = torch.mean(z_ano, dim=0)
     
# 两类中心远离,最大化dist
dist = torch.sum((nor_center - ano_center) ** 2)
     
# 类内聚集，最小化nor_dis + ano_dis
nor_dis = torch.sum((nor_center - z_nor) ** 2)
ano_dis = torch.sum((ano_center - z_ano) ** 2)
     
# 综合以上两点，整体的loss
loss = (nor_dis + ano_dis) - dist

如果只是按照以上的loss训练，会发现类间距离dist会不断增大，而忽略了nordis和anodis的最小化。为了解决上述问题，引入一个超参Lambda， 调节网络的优化方向：

Lambda = 0.05
if dist.item() > max_dis:
    Lambda = 0.9           
loss = Lambda * (nor_dis + ano_dis) - (1 - Lambda) * dist

刚开始的时候，Lambda=0.05，网络的优化方向更侧重于将dist变大，将两个类簇分开。当dist大到预设的最大值maxdis, 就调整Lambda=0.9，让网络的优化方向更侧重于减小(nordis+ano_dis), 即让每个点往它的类簇中心靠拢。在训练过程中，观察到一些很有意思的现象：刚开始的时候，所有的样本都聚集在（0,0,0）点附*，两类中心的距离dist自然也是非常接*于0，经过多轮训练之后，网络才开始很明显地将两簇的中心分开。在其中几条kpi中，正常样本和异常样本比较相似，甚至要经过1000轮以上训练之后才能将两类分开。

实际结果与设想的结果不尽相同，但是对异常检测效果影响不大。实际训练和检测的结果如下图所示

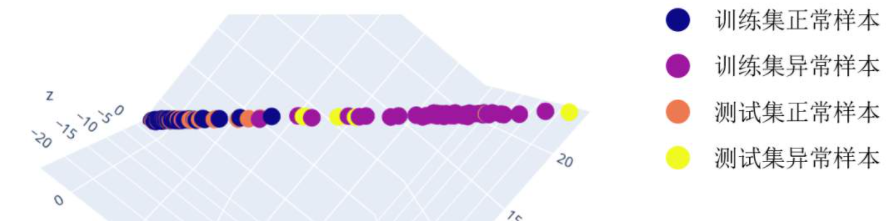
  • trick1调整不同的滑动窗口大小和选取标签的位置

在实际应用中，异常检测要求及时性。当异常发生时，越快检测出异常越好。所以一般在滑动窗口采样时，都是取窗口的最后一个点的标签作为这个窗口的标签。这样做的话，在检测一个点是否为异常时， 只能根据它本身以及过去的数据来检测。然而在本次比赛中，并不要求及时响应。所以这里我为了提高检检测效果，“不择手段”地引入了未来的数据。根据不同的KPI， 选择不同的滑动窗口大小和标签在窗口里的位置。

  • trick2 判断异常的方式

对于测试集的每一个样本，直接根据它到正常簇和异常簇的哪一簇中心的距离更*，它到哪一簇的中心更*，就把它判定为哪一类。后来发现这种判断方式不够用：对于一些训练集里没有出现过的异常样本， 虽然它距离正常簇中心更*，却比大多数正常样本更加远离正常簇中心。基于以上观察， 判断异常的方式修改为：计算每个测试样本到正常簇中心的距离d,确定一个阈值a 当d>a就判定该样本为异常。

这里可以用一种相邻异常点的判断方法，如果异常检测算法在该连续异常区间开始后的 不晚于T 个时间点内检测到了该连续异常区间，就认为此异常检测算法成功地检测到了整段连续异常区间，因此该异常区间内的每一个异常点都算作一次true positive（TP）；否则，该连续异常区间内的每一个异常点都算作一次false negative（FN）。就举下图为例，第一行是真实标签。如果模型输出score>=0.5判定为异常， 那么得到的结果是point-wise alert这一行的结果。采用以上的评分方法， 经过调整之后的结果为adjusted alert这一行的结果：

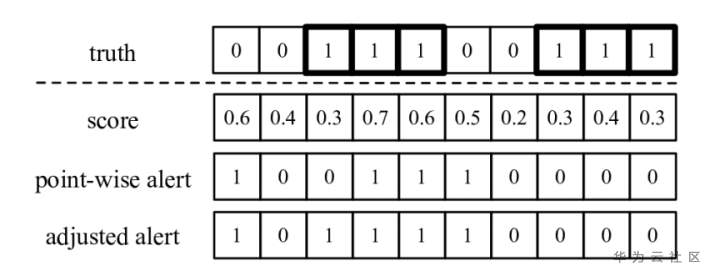
这样的评分方式是有实际意义的。在实际的运维过程中， 一旦异常检测算法检测出异常并产生警报， 这时就有人工介入， 那么后续发生的异常也就有人工干预了，那就相当于这一段连续的异常，都有人工介入处理。

3） 基于Transformer掩码重建的时序数据异常检测算法（pyTorch）

有关Transformer的基础知识可以参考我的另一篇学习笔记
VoidOc：【深度学习】Transformer65 赞同 · 3 评论文章

a) 如何重建

对于大部分重建的时间步而言，模型事实上是从整段时间序列中取一段长度来重建下一步（LSTM信息传播的步数是有限的）。重建序列是将一步步的预测拼接而成一段完整的序列，如图 3(a)所示。也就是说，这一过程是单向的，仅有重建时间步之前的数据影响了重建的这一时间步。

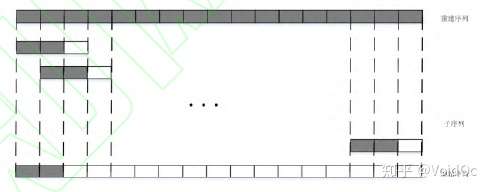图3(a)

而 Transformer 与传统的基于 RNN 的模型不同。一次性读取整段时序数据。在 NLP 任务中，模型可以从一个单词的左右文字学习这个单词的作用。因此设想了一种新的数据输入输出的方式，即图 3（b）。获取一段完整序列并分割成小序列时，不是重建这一段小序列的最后一节数据，而是预测这一段小序列的中间一节数据。这样就可以使用重建数据的左右两边的信息来重建。

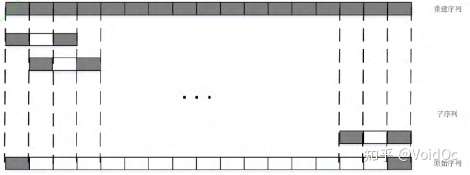图3(b)

b) 模型结构

受 Mask Language Modelling 启发，有人提出Mask Time Series Modeling ，一种基于时序数据的重建。 模型结构如下：

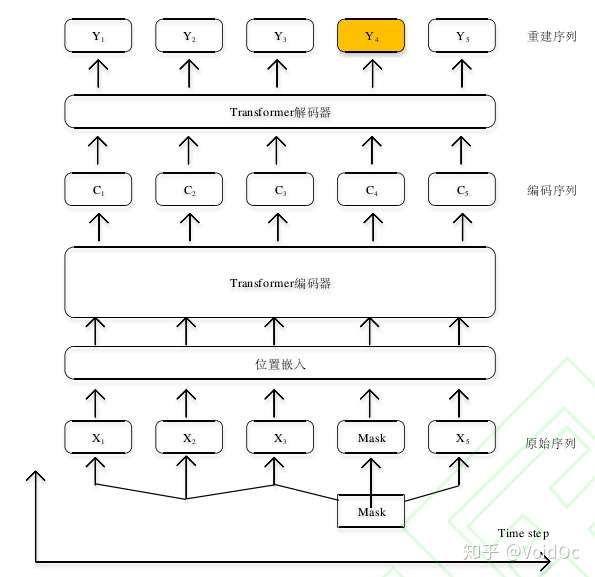掩码时序建模

对于输入序列X = [ 1, 2,…, ]，选择其中将要重建的时间步如 4用[mask]标志代替，从 接 下 来 的 模 型 中 屏 蔽 掉。经 过 一 层 position encoding 进入如上的 Transformer encoder 得到编码后的序列 encoded sequence 也就是上文提到的memory（但与一般的 memory 不同，此时的 memory不含要重建的 4）.再经过一个简单的 decoder 之后获取序列。损失函数定义为被屏蔽的 4预测值与真实值之间。换言之， mask time series modeling 是从被 mask 的时间步两边的数据或者说上下文数据重建时间步。这充分利用了 Transformer 无向性的特点。同时，综合利用上下文信息，也可提高重建的精度。

c) 异常检测效果

时序数据异常检测数据集的标注需要昂贵的专家成本，尤其是详细标注了异常发生的开始和结束时刻的数据集。这类数据集规模通常较小，因此检验算法效果存在一定偶然性。

基于重建误差的异常检测，要求模型在输入正常数据时重建误差较小，输入异常数据时重建误差较大；下面我们可以看一下孟恒宇同学在他的论文里对不同工况的存储数据集进行重建效果的对比：

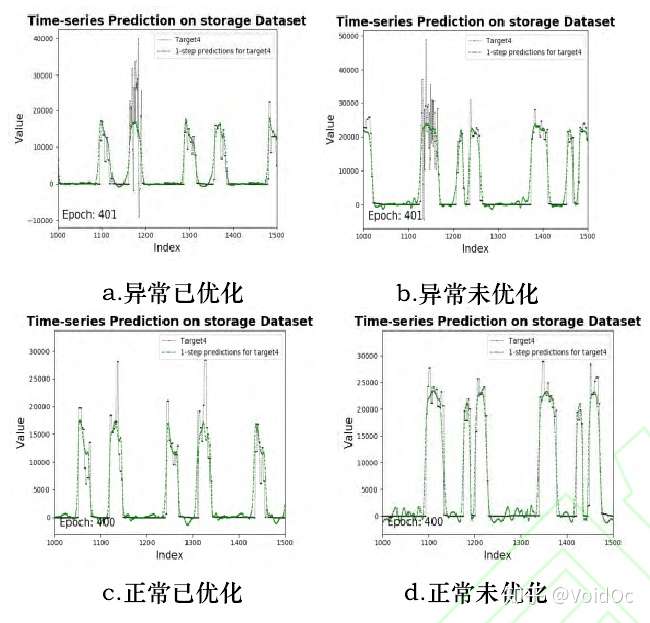四个工况子集上传感器的数据的Transformer重建结果对比，绿色为预测波形

可以看出优化后的数据比未优化的数据更*稳波动更小，而异常数据比跟正常数据多了一小段激剧上下波动的异常。

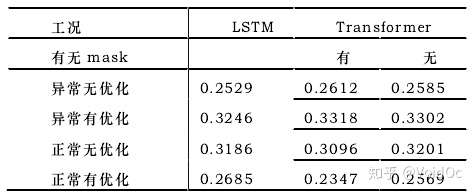不同工况下LSTM与Transformer的绝对误差对比

上表为四个子集上的重建结果的绝对误差对比。可以看到 Transformer 方法在有异常的数据集上重建的绝对误差更大 ，这 说 明 面 对 异 常 发 生 时Transformer 的表现更鲁棒。优化工况的周期性更明显，本文方法效果显著提高。

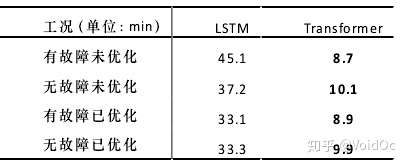不同工况下LSTM与Transformer的训练耗时对比

可以看出，由于 Transformer 放弃了 LSTM 的序列式推进，其 self-attention 模块完全可以并行，因此用时普遍较少，最多可以节约 80.7%的时间，同时异常检测 F1 score 达到0.78。

d) 补充

需要强调一下Multi-head 机制在这个时序数据任务中几乎没有发挥作用，可能是因为数据维度过少，只有 25 或 55维，而一般的 NLP 任务的词一般会嵌入 512 维度的词向量空间。

5. 资源 Useful links

 
posted on 2022-07-06 16:19  风生水起  阅读(720)  评论(0)  编辑  收藏  举报
Copyright © 2024 风生水起
Powered by .NET 9.0 on Kubernetes Powered By: 博客园