原标题 | 10 Gradient Descent Optimisation Algorithms + Cheat Sheet
作者 | Raimi Karim in Towards Data Science
译者 | 斯蒂芬•二狗子(沈阳化工大学)、intelLigenJ(算法工程师)、星期五、莱特•诺顿、沧海一升
本文编辑:王立鱼
英语原文:https://towardsdatascience.com/10-gradient-descent-optimisation-algorithms-86989510b5e9

梯度下降是一种寻找函数极小值的优化方法,在深度学习模型中常常用来在反向传播过程中更新神经网络的权值。
在这篇文章中,我会总结应用在目前较为流行深度学习框架中的常见梯度下降算法(如TensorFlow, Keras, PyTorch, Caffe)。本文之目的是为了方便理解和掌握这些内容,因为除此之外总结并不多,而且它可以作为你从零基础入门的“小抄”。
在一个线性回归问题中,我已经用梯度下降实现了SGD, momentum, Nesterov, RMSprop 以及Adam,获取代码(Java)
梯度下降优化算法功能是什么?
通过梯度下降,优化算法可以在如下三个主要方面起作用:
1、修改学习率成分,α, 或
2、修改梯度成分 ∂L/∂w
3、或二者兼有
且看如下方程1:
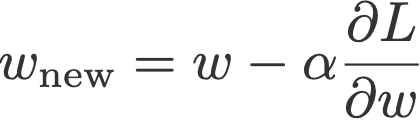
方程1:随机梯度下降中的各种量
学习率调度器vs梯度下降优化
主要的不同在于梯度下降优化让学习率乘以一个因子,该因子是梯度的函数,以此来调整学习率成分,然而学习率调度器让学习率乘以一个恒为常数或是关于时间步幅的函数的因子,以此来更新学习率。
第1种方法主要通过在学习率(learning rate)之上乘一个0到1之间的因子从而使得学习率降低(例如RMSprop)。第2种方法通常会使用梯度(Gradient)的滑动平均(也可称之为“动量”)而不是纯梯度来决定下降方向。第3种方法则是结合两者,例如Adam和AMSGrad。
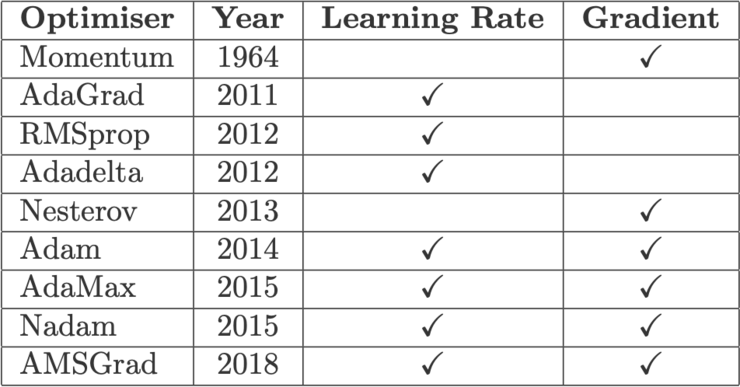
Fig.2:各类梯度下降优化算法、其发表年份和用到的核心思路。
Fig.3 自上而下展示了这些优化算法如何从最简单的纯梯度下降(SGD)演化成Adam的各类变种的。SGD一开始分别往两个方向演变,一类是AdaGrad,主要是调整学习率(learning rate)。另一类是Momentum,主要调整梯度(gradient)的构成要素(译注:原文此处写反了)。随着演化逐步推进,Momentum和RMSprop融为一体,“亚当”(Adam)诞生了。你可能觉得我这样的组织方式抱有异议,不过我目前一直是这样理解的。
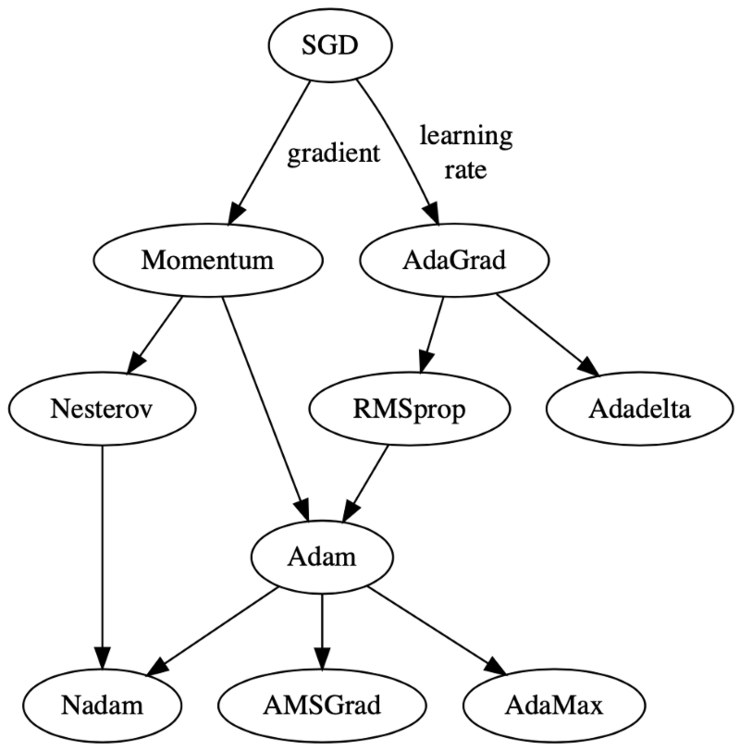
Fig.3:各类优化算法的演化图(gist)
符号表示
- t - 迭代步数
- w - 我们需要更新的权重及参数
- α - 学习率
- ∂L/∂w - L(损失函数)对于w的梯度
- 我统一了论文中出现过的希腊字母及符号表示,这样我们可以以统一的“演化”视角来看这些优化算法
1. 随机梯度下降(Stochastic Gradient Descend)
最原始的随机梯度下降算法主要依据当前梯度∂L/∂w乘上一个系数学习率α来更新模型权重w的。
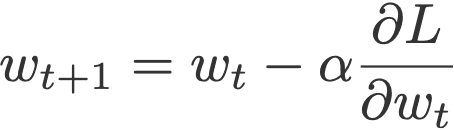
2. 动量算法(Momentum)
动量算法使用带有动量的梯度(梯度的指数滑动平均,Polyak, 1964)而不是当前梯度来对w进行更新。在后续的文章中你会看到,采用指数滑动平均作为动量更新的方式几乎成为了一个业内标准。

其中
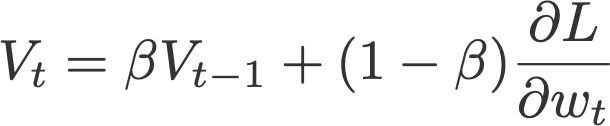
并且V初始化值为0。β一般会被设置为0.9。
值得注意的是,很多文章在引用Momemtum算法时会使用Ning Qian, 1999的文章。但这个算法的原出处为Sutskever et al。而经典动量算法在1964年就被Polyak提出了,所以上文也引用了Polyak的文章。(感谢James指出了这一点)
3.Nesterov加速梯度下降法(NAG)
在Polyak提出了动量法之后(双关:Polyak势头正盛),一个使用Nesterov加速梯度下降法(Sutskever et al., 2013)的类似更新方法也被实现了。此更新方法使用V,即我称之为投影梯度的指数移动平均值。

其中
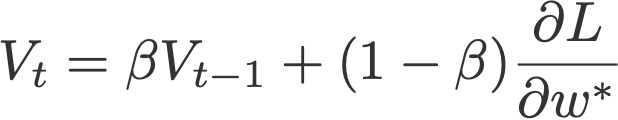
且V 初始化为0。
第二个等式中的最后一项就是一个投影梯度。这个值可以通过使用先前的速度“前进一步”获得(等式4)。这意味着对于这个时间步骤t,我们必须在最终执行反向传播之前执行另一个前向传播。这是步骤:
1.使用先前的速度将当前权重w更新为投影权重w*
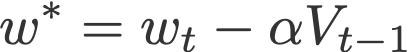
(等式4)
2. 使用投影权重计算前向传播
3.获得投影梯度∂L/∂w*
4.计算相应的V和w
常见的默认值:
- β = 0.9
请注意,原始的Nesterov 加速梯度下降法论文( Nesterov, 1983 )并不是关于随机梯度下降,也没有明确使用梯度下降方程。因此,更合适的参考是上面提到的Sutskever等人的出版物。在2013年,它描述了NAG在随机梯度下降中的应用。(再一次,我要感谢James对HackerNews的评论中指出这一点。)
4. 自适应学习率算法(Adagrad)
自适应梯度算法,也称AdaGrad算法(Duchi等,2011),通过将学习率除以S的平方根来研究学习率分量,其中S为当前和过去平方梯度的累积和(即直到时间t)。请注意,和SGD算法相同,自适应学习率算法中的梯度分量也保持不变。

其中,
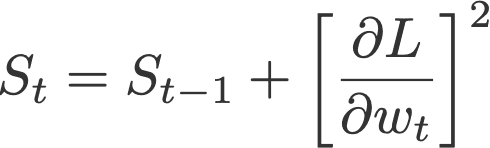
并将S的初始值置0.
请注意,这里在分母中添加了ε。Keras称之为模糊因子,它是一个小的浮点值,以确保我们永远不会遇到除零的情况。
默认值(来自Keras):
- α = 0.01
- ε = 10⁻⁷
5. 均方根传递算法(RMSprop)
均方根传递算法,也称RMSprop算法(Hinton等,2012),是在AdaGrad算法上进行改进的另一种自适应学习率算法。 它使用指数加权平均计算,而不是使用累积平方梯度和。

其中,
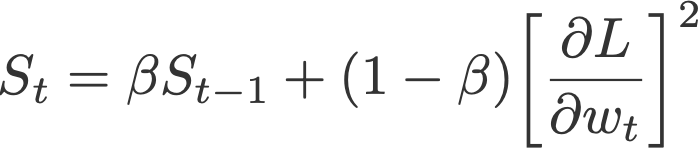
并将S的初始值置0.
默认值(来自Keras):
- α = 0.001
- β = 0.9 (本文作者推荐)
- ε = 10⁻⁶
6. 自适应增量算法(Adadelta)
与RMSprop算法类似,Adadelta(Zeiler,2012)是在AdaGrad算法的基础上针对学习率进行改进的一种自适应算法。Adadelta应该是是“自适应增量”的缩写,其中,delta表示当前权重与新更新权重之间的差值。
Adadelta算法和RMSprop算法的区别,在于Adadelta算法中用delta的指数加权平均值D来替代原来在Adadelta算法中的学习率参数。
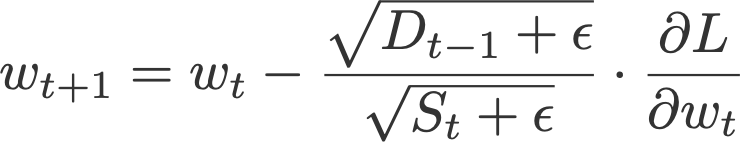
其中,
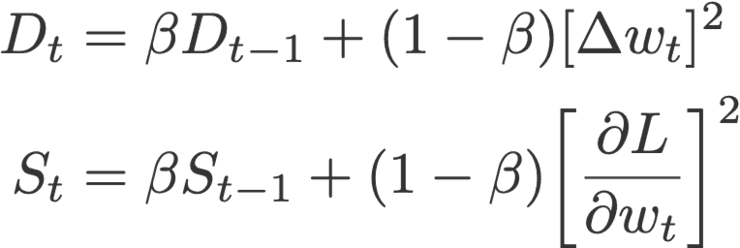
并把D和S的初始值置0. 此外,
默认值(来自Keras):
- β = 0.95
- ε = 10⁻⁶
7. 适应性矩估计算法(Adam)
适应矩估计算法,也称Adam算法(Kingma&Ba,2014),是一种将动量和RMSprop结合使用的算法。它通过
(i) 使用梯度分量V,梯度的指数移动平均值(如动量)和
(ii)将学习率α除以S的平方根,平方梯度的指数移动平均值(如在RMSprop中)来学习率分量而起作用。
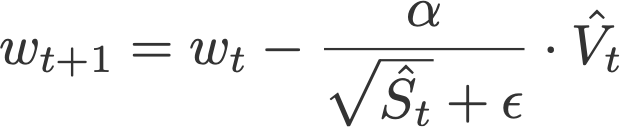
其中
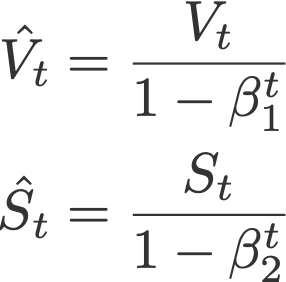
是偏差修正,并有
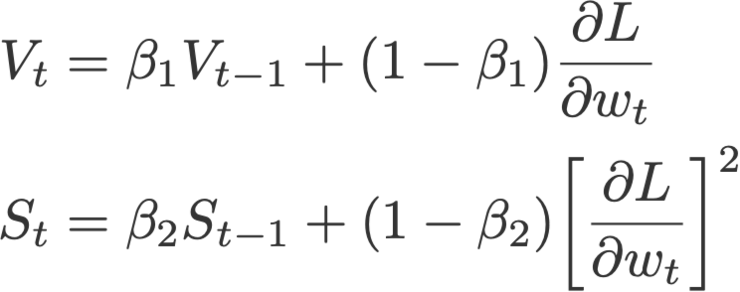
V和S的初始值置0.
作者推荐的默认值:
- α = 0.001
- β₁ = 0.9
- β₂ = 0.999
- ε = 10⁻⁸
8. AdaMax算法
AdaMax(Kingma&Ba,2015)是使用无限范围(因此为'max')的由Adam算法的原作者们对其优化器进行改编的一种算法。V是梯度的指数加权平均值,S是过去p阶梯度的指数加权平均值,类似于最大函数,如下所示(参见论文收敛证明)。
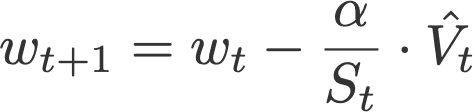
其中
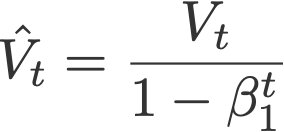
是对V的偏差修正,并有
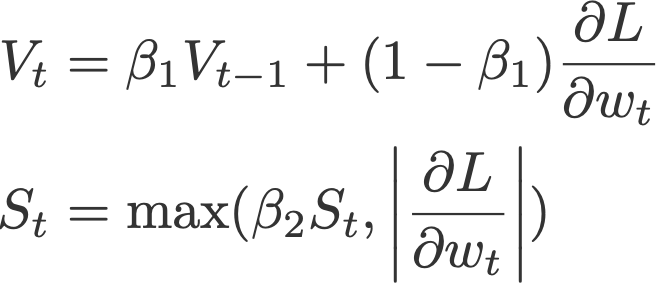
V和S的初始值置0.
作者推荐的默认值:
- α = 0.002
- β₁ = 0.9
- β₂ = 0.999
9. Nadam算法
Nadam一词由(Dozat,2015)是Nesterov和Adam优化器的名称拼接而成。Nesterov组件在Nadam算法中对学习率产生了更强的约束,同时对梯度的更新也有更直接的影响。一般而言,在想使用带动量的RMSprop,或者Adam的地方,大多可以使用Nadam取得更好的效果。
Adam优化器也可以写成:
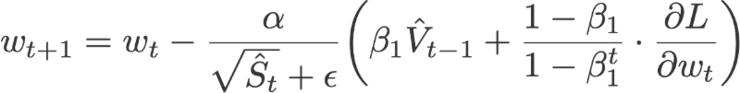
公式5:Adam优化器的权重更新
Nadam利用Nesterov通过将上面等式中的前一时刻的V_hat替换为当前时刻的V_hat,实现了提前一步更新梯度:
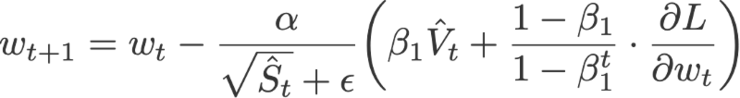
其中
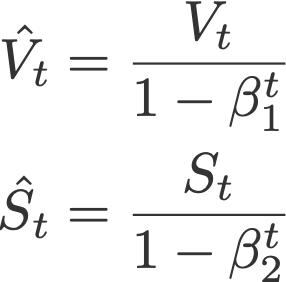
并有
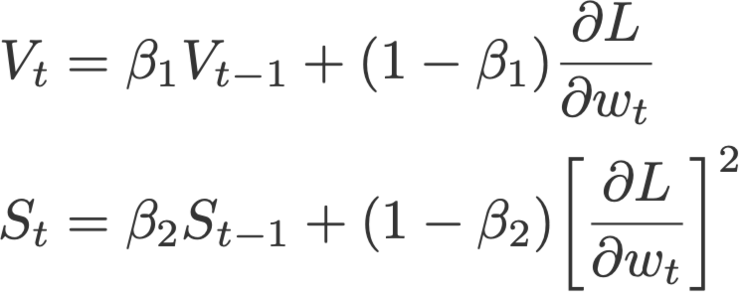
V和S初始值置0.
默认值(取自Keras):
- α = 0.002
- β₁ = 0.9
- β₂ = 0.999
- ε = 10⁻⁷
10. AMSGrad算法
Adam算法的另一个变体是AMSGrad算法(Reddi等,2018)。该算法重新访问Adam中的自适应学习速率组件并对其进行更改以确保当前S始终大于前一时间步长。

其中
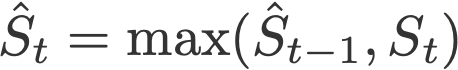
此外
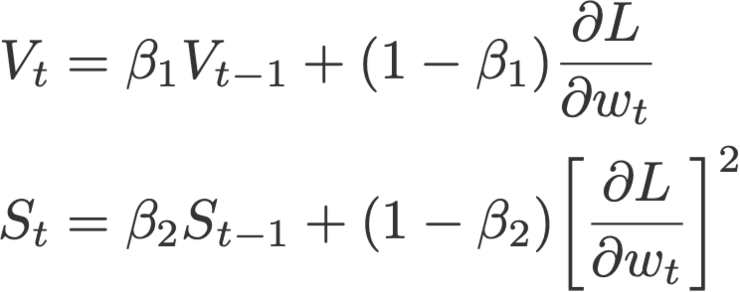
V和S初始值置0.
默认值(取自Keras):
- α = 0.001
- β₁ = 0.9
- β₂ = 0.999
- ε = 10⁻⁷
直觉
我想和你们分享一些直观的见解,为什么梯度下降法优化器对梯度部分使用的是指数移动平均值(EMA),对学习率部分使用均方根(RMS)。
为什么要对梯度取指数移动平均?
我们需要使用一些数值来更新权重。我们唯一有的数值呢就是当前梯度,所以让我们利用它来更新权重。
但仅取当前梯度值是不够好的。我们希望我们的更新是(对模型来说,是)“更好的指导”。让我们考虑(每次更新中)包括之前的梯度值。
将当前梯度值和过去梯度信息的结合起来一种方法是,我们可以对过去和现在的所有梯度进行简单的平均。但这意味着每个梯度的权重是相等的。这样做是反直觉的,因为在空间上,如果我们正在接近最小值,那么最近的梯度值可能会提供更有效的信息。
因此,最安全的方法是采用指数移动平均法,其中最近的梯度值的权重(重要性)比前面的值高。
为什么要把学习速率除以梯度的均方根呢?
这个目的是为了调整学习的速率。调整为了适应什么?答案是梯度。我们需要确保的是,当梯度较大时,我们希望更新适当缩小(否则,一个巨大的值将减去当前的权重!)
为了到达这种效果,让我们学习率α除以当前梯度得到一个调整学习速率。
请记住,学习率成分必须始终是正的(因为学习率成分,当乘以梯度成分,后者应该有相同的符号)。为了确保它总是正的,我们可以取它的绝对值或者它的平方。当我们取当前梯度的平方,可以再取平方根"取消"这个平方。
但是就像动量的思路一样,仅仅采用当前的梯度值是不够好的。我们希望我们的训练中的(每次)更新update都能更好的指导(模型)。因此,我们也需要使用之前的梯度值。正如上面所讨论的,我们取过去梯度的指数移动平均值('mean square') ,然后取其平方根('root') ,也就是'均方根'(RMS)。除了 AdaGrad (采用累积的平方梯度之和)之外,本文中所有的优化器都会对学习速率部分进行优化。
备忘单
(上述要点)
如果有什么不妥之处,或者如果这篇文章中的内容可以再改进,请与我联系!?
参考
梯度下降优化算法概述(ruder.io)
为什么Momentum真的有效
这是一个关于动量的流行故事:梯度下降是一个人走在山上。
感谢Ren Jie,Derek,William Tjhi,Chan Kai,Serene和James对本文的想法,建议和更正。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号