两者都可以用来衡量两个概率分布之间的差异性。JS散度是KL散度的一种变体形式。
KL散度:
也称相对熵、KL距离。对于两个概率分布P和Q之间的差异性(也可以简单理解成相似性),二者越相似,KL散度越小。
KL散度的性质:
●非负性。即KL散度大于等于零。
●非对称性。即运算时交换P和Q的位置,得到的结果也不一样。(所以这里严格来讲也不能把KL散度称为KL距离,距离一定符合对称性,所以要描述准确的话还是建议用KL散度来表述)
离散分布公式:
连续分布公式:
python代码实现:
#KL_divergence
import numpy as np
import scipy.stats
P=np.array([1/4,1/2,1/4,1/4])
Q=np.array([1/3,1/3,1/6,1/6])
def KL_divergence(P,Q):
return scipy.stats.entropy(P,Q)
print(KL_divergence(P,Q)) # 0.04369212068196553
print(KL_divergence(P,Q)) # 0.04369212068196553
JS散度:
JS散度是KL散度的一种变体,与KL散度相似,P和Q越相似,JS散度越小。
JS散度的性质:
●JS散度的值域范围是[0,1],完全相同为0,完全相反为1。相较于KL,对相似度的判别更确切了。
●对称性。通过公式可以看出交换了P和Q的位置计算结果仍然一样。(个人认为这种JS散度的出现就是为了解决KL散度不对称的问题)
python代码实现:
#JS_divergence
import numpy as np
import scipy.stats
P=np.array([1/4,1/2,1/4,1/4])
Q=np.array([1/3,1/3,1/6,1/6])
R=np.array([1/10,3/10,4/10,2/10])
def JS_divergence(P,Q):
M=(P+Q)/2
return 0.5*scipy.stats.entropy(P, M)+0.5*scipy.stats.entropy(Q, M)
print(JS_divergence(P,Q)) # 0.011598863066818382
print(JS_divergence(Q,P)) # 0.011598863066818382
————————————————
在看论文《Detecting Regions of Maximal Divergence for Spatio-Temporal Anomaly Detection》时,文中提到了这三种方法来比较时间序列中不同区域概率分布的差异。
KL散度、JS散度和交叉熵
三者都是用来衡量两个概率分布之间的差异性的指标。不同之处在于它们的数学表达。
对于概率分布P(x)和Q(x)
1)KL散度(Kullback–Leibler divergence)
又称KL距离,相对熵。
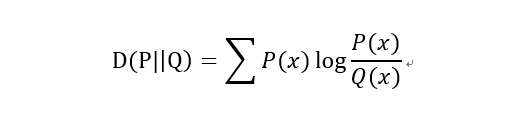
当P(x)和Q(x)的相似度越高,KL散度越小。
KL散度主要有两个性质:
(1)不对称性
尽管KL散度从直观上是个度量或距离函数,但它并不是一个真正的度量或者距离,因为它不具有对称性,即D(P||Q)!=D(Q||P)。
(2)非负性
相对熵的值是非负值,即D(P||Q)>0。
2)JS散度(Jensen-Shannon divergence)
JS散度也称JS距离,是KL散度的一种变形。
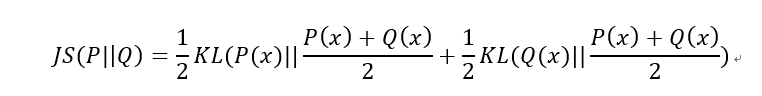
但是不同于KL主要又两方面:
(1)值域范围
JS散度的值域范围是[0,1],相同则是0,相反为1。相较于KL,对相似度的判别更确切了。
(2)对称性
即 JS(P||Q)=JS(Q||P),从数学表达式中就可以看出。
3)交叉熵(Cross Entropy)
在神经网络中,交叉熵可以作为损失函数,因为它可以衡量P和Q的相似性。
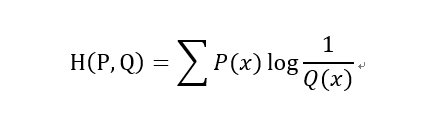
交叉熵和相对熵的关系:
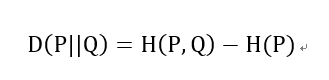
以上都是基于离散分布的概率,如果是连续的数据,则需要对数据进行Probability Density Estimate来确定数据的概率分布,就不是求和而是通过求积分的形式进行计算了。
补充:信息熵、交叉熵与KL散度
信息量
在信息论与编码中,信息量,也叫自信息(self-information),是指一个事件所能够带来信息的多少。一般地,这个事件发生的概率越小,其带来的信息量越大。

从编码的角度来看,这个事件发生的概率越大,其编码长度越小,这个事件发生的概率越小,其编码长度就越大。但是编码长度小也是代价的,比如字母'a'用数字‘0'来表示时,为了避免歧义,就不能有其他任何以‘0'开头的编码了。
因此,信息量定义如下:
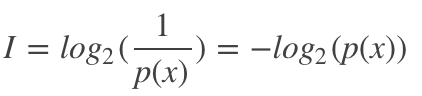
信息熵
信息熵是指一个概率分布p的平均信息量,代表着随机变量或系统的不确定性,熵越大,随机变量或系统的不确定性就越大。从编码的角度来看,信息熵是表示一个概率分布p需要的平均编码长度,其可表示为:
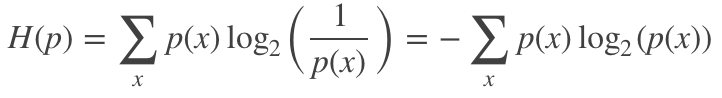
交叉熵
交叉熵是指在给定真实分布q情况下,采用一个猜测的分布p对其进行编码的平均编码长度(或用猜测的分布来编码真实分布得到的信息量)。
交叉熵可以用来衡量真实数据分布于当前分布的相似性,当前分布与真实分布相等时(q=p),交叉熵达到最小值。
其可定义为:
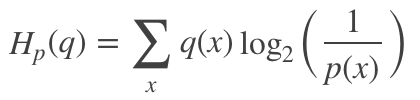
因此,在很多机器学习算法中都使用交叉熵作为损失函数,交叉熵越小,当前分布与真实分布越接近。此外,相比于均方误差,交叉熵具有以下两个优点:
在LR中,如果用均方误差损失函数,它是一个非凸函数,而使用交叉熵损失函数,它是一个凸函数;
在LR中使用sigmoid激活函数,如果使用均方误差损失函数,在对其求残差时,其表达式与激活函数的导数有关,而sigmoid(如下图所示)的导数在输入值超出[-5,5]范围后将非常小,这会带来梯度消失问题,而使用交叉熵损失函数则能避免这个问题。

KL散度
KL散度又称相对熵,是衡量两个分布之间的差异性。从编码的角度来看,KL散度可表示为采用猜测分布p得到的平均编码长度与采用真实分布q得到的平均编码长度多出的bit数,其数学表达式可定义为:
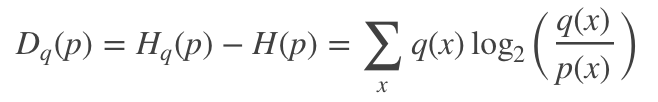
一般地,两个分布越接近,其KL散度越小,最小为0.它具有两个特性:
非负性,即KL散度最小值为0,其详细证明可见[1] ;
非对称性,即Dq(p)不等于Dp(q) ; KL散度与交叉熵之间的关系
在这里,再次盗用[1]的图来形象地表达这两者之间的关系:
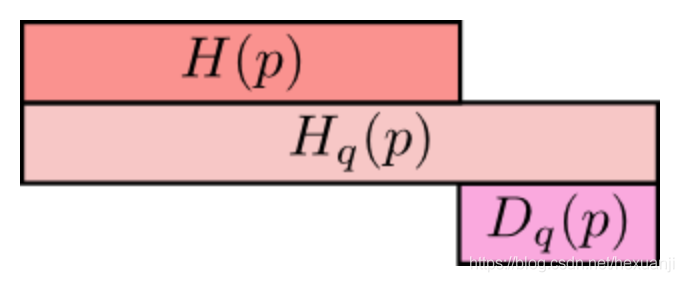
最上方cH(p)为信息熵,表示分布p的平均编码长度/信息量;
中间的Hq(p)表示用分布q表编码分布p所含的信息量或编码长度,简称为交叉熵,其中Hq(p)>=H(p)
;最小方的Dq(p)表示的是q对p的KL距离,衡量了分布q和分布p之间的差异性,其中Dq(p)>=0;
从上图可知,Hq(p) = H(p) + Dq(p)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号