NOI2015 荷马史诗

题目链接：NOI2015 荷马史诗

在写题解之前先扯一些闲话

初识这题是在hzwer的博客上，他写的一篇类似于回忆录中提到了这题。其实OI中有很多类似于哈夫曼的知识——它们看起来看起来不是那么重要，但是如果一旦用到，对于那些不知道的人便是”灭顶之灾“，OI这玩意，很多时候，真的有一部分运气的成分，五六场比赛，不能出现一丝错误，虽然不乏奇迹，但更多的，却是无奈。

哈夫曼编码是基于哈夫曼树的一种编码方式，注意到题目有这样一句话

“对于任意的 1 ≤ i, j ≤ n ， i ≠ j ，都有：si不是sj的前缀。”

然后我们在来看到一个哈夫曼编码的例子：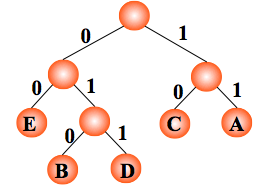

 

大家所熟知的哈夫曼树基本上都是二叉的，即用二进制表示

而题目中要求的是k进制，这基本上是一样的

在上面的例子中，所有有字母的格子都代表着未加密的字符，由根节点走向它们的路径上的数组成了这个字符的编码，由于每个字符没有子树，所以便不会出现有编码是其它编码的前缀

由于此时的编码是k进制的，所以每次合并是将k个节点合并成一个节点，

但是这样就会有一个问题：在合并是会出现一些空的节点

再推一下会发现：将n个节点合并成1个节点，每次将k个节点合并成一个节点，最终会有$(n-1) \ mod\ (k-1)$个节点单独空着无法合并

所以我们要补一些w为0的节点，若$(n-1) \ mod\ (k-1)!=0$,则需补充$(k-1)-(n-1)\ mod \ (k-1)$个节点

最终要求的高度就是所构造的哈夫曼树的高度

哈夫曼树的合并有点类似于NOIp2004石子合并，不过这里由于$n\leq10^5$于是可以直接用优先队列写过去

#include<iostream>
#include<string>
#include<string.h>
#include<stdio.h>
#include<algorithm>
#include<vector>
#include<queue>
#include<map>
using namespace std;
struct node{
    long long w;int h;
    bool operator <(const node p)const
    {
        return ((w>p.w) || ((w==p.w) && (h>p.h)));
    }
};
priority_queue<node> q;
int n,k;
int main()
{
    scanf("%d%d",&n,&k);
    int i;
    for (i=1;i<=n;i++)
    {
        long long w;
        scanf("%lld",&w);
        q.push((node){w,1});
    }
    int cnt=0;
    if ((n-1)%(k-1)!=0) cnt=((k-1)-((n-1)%(k-1)));
    for (i=1;i<=cnt;i++) q.push((node){0,1});
    long long ans=0;cnt+=n;
    while (cnt>1)
    {
        long long sumw=0;int maxh=0;
        for (i=1;i<=k;i++)
        {
            node p=q.top();q.pop();
            sumw+=p.w;maxh=max(p.h,maxh);
        }
        q.push((node){sumw,maxh+1});cnt-=(k-1);
        ans+=sumw;
    }
    printf("%lld\n",ans);
    node p=q.top();
    printf("%d\n",p.h-1);
    return 0;
}