位运算、整数等
又是一些零零散散的东西。
文章目录
为什么宏INT_MIN要写成-2147483647-1
因为c语言中 -其实是个运算符,实际操作是取反+1, -2147483648会产生错误。
c语言整数类型转换大致规则
长型数据转化为短型数据,直接截断,保留低位数据。
1.短型数据转化为长型数据,如果是有符号数,补符号位,如果是无符号数,补0.
2.有符号数转换为无符号数或者无符号数转换为有符号数,不改变数值,只改变解释方式。
3.即改变长度,也改变符号时,先改变长度,再改变符号。
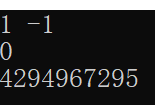
例子:
#include <stdio.h>
int main()
{
int n = 1, b = -1;
unsigned nu = (unsigned)n, bu = (unsigned)b;
printf("%d %d\n", nu, bu);//有符号无符号之间转换,只改变解释数的方式,而数在内存中的值不变。
int num = 512;
char ch = (char)num;//截断数字,直接去掉高位,保留低位
printf("%u\n", ch);
num = 0xff;
//先改变长度,再改变符号。
//再vc中,char默认是有符号类型,所以扩展时进行有符号扩展
//有符号扩展即,扩展位时,左边补最高位的值,无符号扩展,即,扩展位时,左边补0,而不管最高位时0是1
//把char*类型指针指向的值显然是ff,最高位是1
//先进行位扩展,补1
//再转换符号,转换成了一个大无符号数。
printf("%lu\n", *((char*)&num));//因为先改变大小,再改变符号。
return 0;
}
输出:
对反码、补码的理解,为什么负数反码加一是补码。补码加法(模数加法)
除INT_MIN外 任意数x的相反数-x.
x补码的实际二进制表示加上-x的补码的实际二进制表示,他们相加的和的二进制位表示为2x的二进制位数。模2x的二进制位数,结果即为0.
x是补码表示的数。
1) -x <==> ~x+1
2) -x <==> 找到 x的二进制位中最右边的1,对这一位左边所有位取反。
反码:假设二进制数有w位,x的反码即为(2w-1)-x即(11…11)B-x
例如四位二进制数1010
w为4
2w - 1 = 24 - 1 = 1111.
1111 - 1010 = 0101 = ~1010.
再比如
五位二进制数00101
w为5
2w - 1 = 25 - 1 = 11111.
11111 - 00101 = 11010 = ~00101.
补码:假设二进制数有w位,x的补码即2w-x即(10…00)B-x。
例如四位二进制数1010
w为4
2w = 24 = 10000.
10000 - 1010 = 0110 = ~1010+1.
再比如
五位二进制数00101
w为5
2w = 25 = 100000.
10000 - 00101 = 11011 = ~00101+1.
对负数来说
[x]补 = 2w - x
[x]反 = (2w - 1)- x
[x]反 + 1 = (2w - 1)- x + 1 = 2w - x = [x]补
所以:负数反码加一为补码
加减法溢出判断
其实都是模数加法
两无符号数相加,最高位产生进位即溢出,最高位不产生进位即不溢出。
两有符号数(补码)相加,最高位产生进位不一定溢出,最高位不产生进位不一定不溢出。
注:
大多数c语言实现,都是用补码表示无符号数。
大多数c语言实现,无符号数和有符号数的加法过程、结果都是一样的,只是解释这些结果的方式不一样。
注:模数加法是可逆的。即x+y无论是否溢出,(x+y)-x==y 都成立。
检测无符号数相加是否溢出的函数。
若两数相加结果正常,即不溢出,返回1,否则返回0。
原理:若两无符号数x,y相加结果溢出,那么结果一定既小于x,又小于y。
证明:略。
参考:csapp
int uadd_ok(unsigned x, unsigned y)
{
return x+y>=x;
}
检测有符号数相加是否溢出的函数。
若两数相加结果正常,即不溢出,返回1,否则返回0。
原理:0与任何数相加都不会溢出;正数与负数相加不会溢出;两正数相加结果不为正发生上溢(正溢),两负数相加结果不为负发生下溢(负溢)。
int tadd_ok(int x, int y)
{
return !(x>0&&y>0&&x+y<=0||x<0&&y<0&&x+y>=0);
}
检测两有符号数想减是否会溢出,不会溢出返回1.
注:-INT_MIN 运算结果是 INT_MIN。
因为对-运算符其实是取反加1。0x80000000取反0x7fffffff 加1还是0x80000000.
补码的取值范围不对称,INT_MIN其实是没有与之绝对值相等的正的INT数的。
这也是limits.h头文件中
#define INT_MIN -INT_MAX-1
INT_MIN这样写的原因。
int tadd_ok(int x, int y)
{
return !(x>0&&y>0&&x+y<=0||x<0&&y<0&&x+y>=0);
}
#include <limits.h>
int tsub_ok(int x, int y)
{
if(y==INT_MIN)
{
if(x<0)
return 1;
else
return 0;
}
return tadd_ok(x,-y);
}
求一些数相乘,它们末尾0的个数
原理:每个合数都可以分解成几个质数相乘的形式
1、 10进制
把所有的数都分解成质因子
有多少对2和5末位就有多少个0
也就是说分解成的这一堆质数中有2的个数和5的个数中小者就是十进制末位0的个数
原理任何数都可以分解位一些质数的乘积
对于质数来说,只有2*5末尾位10末位一个0
若是两对2*5 2*5*2*5=100末位2个0
以此类推
3、16进制(猜想,等有空验证)
把所有数分解成一堆质数
十六进制0x10(十进制16),质数的话只能是四个2相乘,也就是说分解成的质数中有多少个4个2
也就是说分解成的质数中2的总个数除4得到的结果十六进制末尾0的个数。
4、8进制(猜想,有待验证)
前面过程与16进制相同,分解成的质数的的2个数除3就是8进制末位0的个数
因为2的3次方是8,8的8进制是10
5、2进制
2进制的2是10,分解成的质数中有多少个2,其末位就有多少个0
6、更普遍的N进数
N一定能分解成一个或几个质数相乘的形式
把这些数分解成质数相乘的形式,这堆质数里出现过几次这几个质数
即这几个质数中出现次数最小者的次数
就是N进制数末位0的个数
把一个数分解成一堆质数,计算其中指定质数的个数。
以求3的个数为例
int cnt=0;
while(!(p%3)){
cnt++;
p /= 3;
}
求n完全分解后k(k为质数)有多少个。
int funZhiyinzi(int n, int k)
{
int cnt=0;
while(n%k == 0)
{
cnt++;
n/=k;
}
return cnt;
}
这样只逐个求出每个数中指定质数的个数,想加,就可以得到这些数相乘末位0的个数了。
用置0、置1 实现 或、异或
参考:csapp
#include <stdio.h>
#include <stdint.h>
#include <inttypes.h>
//功能:按位置1 如果y中的位是1, 把x中对应的位也置为1
//para1: x
//para1: y
//return: x对应位置1后的结果
int32_t bis(int32_t x, int32_t y)
{
return x|y;
}
//功能:按位置1 如果y中的位是1, 把x中对应的位置为0
//para1: x
//para1: y
//return: x对应位置0后的结果
int32_t bic(int32_t x, int32_t y)
{
return x&~y;
}
//用bis和bic实现或
int32_t or(int32_t x, int32_t y)
{
return bis(x,y);
}
//用bis和bic实现异或
//x^y <==> x&~y | y&~x
//解释:如果x,y中有且只有一个为1,则x异或y为1
//x,y中有且只有一个为1即 x为1y为0 或 x为0y为1
//x为1 y为0时 x&~y为1
//x为0 y为1时 y&~x为1
//x为1y为0 或 x为0y 即为 x&~y | y&~x
int32_t xor_or(int32_t x, int32_t y)
{
return bis(bic(x,y), bic(y,x));
}
int main()
{
printf("0|0==%d\n", or(0,0));
printf("0|1==%d\n", or(0,1));
printf("1|0==%d\n", or(1,0));
printf("1|1==%d\n", or(1,1));
printf("0^0==%d\n", xor_or(0,0));
printf("0^1==%d\n", xor_or(0,1));
printf("1^0==%d\n", xor_or(1,0));
printf("1^1==%d\n", xor_or(1,1));
return 0;
}
水题:和一个数最接近的二进制形式1个数相同的数
题目描述
给定一个正整数N,求出一个正整数M,M大于N,且二进制下M与N的“1”的个数相同,在所有满足条件的M中,将最小的一个输出
输入
第一行输入为整数T(T<60),表示T组测试数据
每组测试数据输入一个正整数N,N<=1e9
输出
每组测试数据输出一个正整数M,且是所有满足条件中最小的一个
样例输入 Copy
3
7
23
14232
样例输出 Copy
11
27
14241
ac代码:
#include <stdio.h>
#include <stdint.h>
#include <inttypes.h>
/*
从左往右找到第一个01 (用小端法表示是从右往左找10)
交换它们的位置
并找出第一个01(小端法10)之前有多少个1
把那么多1全部挪到最左边(小端法是最右边),第一个01(小端法10)之前的其余位为0
*/
uint32_t haha(uint32_t a)
{
uint8_t binstr[33]; binstr[32]='\0';//以小端法表示
for(uint8_t i=0;i<32;i++)//把整数转换成一个数组,每个二进制位代表一个元素
{
if((a>>i) & 1)
binstr[i]=1;
else
binstr[i]=0;
}
uint8_t wz10=0;
for(;;wz10++)//找到第一个01的位置,用小端法表示是10
{
if(binstr[wz10]==1 && binstr[wz10+1]==0)
break;
}
uint8_t num1=0;
for(uint8_t i=0;i<wz10;i++) //找出 01(小端法10)之前有多少个1
{
if(binstr[i])
num1++;
}
uint8_t t=binstr[wz10];binstr[wz10]= binstr[wz10+1];binstr[wz10+1]=t;//交换01(小端法10)的位置
for(uint8_t i=0;i<num1;i++)//把01(小端法10)之前的1全挪到最左边(小端法是最右边)
{
binstr[i]=1;
}
for(;num1<wz10;num1++)//比 01(小端法10)之前的其他位全置为0
binstr[num1]=0;
a=0;
for(uint8_t i=0;i<32;i++)//把数组转换为数
{
a=a|(binstr[i]<<i);
}
return a;
}
int main()
{
uint8_t t;
scanf("%"SCNu8, &t);
for(uint8_t i=0; i<t ; i++)
{
uint32_t k;
scanf("%"SCNu32, &k);
printf("%"PRIu32"\n", haha(k));
}
return 0;
}
(两个质数的乘积)(的因子)(只有这两个质数)…括号代表断句
我还是不太明白为什么从2开始找到的第一个因子是质数
想想好像是那样
可是想不出来严谨的证明
题目描述
周末又要来临了,为了让大家可以在周末来临之际有个轻松的心情 ,每到周五,学院会为同学们准备一节时长为45分钟的趣味小课堂。在课堂中老师会给同学们布置一道简单题,让大家可以轻松A掉它。本周五布置的题目是给定一个正整数K,K为某两个质数的乘积,请同学们求出其中较大的那个质数为多少。
输入
第一行输入为整数T(T<100),表示T组测试数据
然后每行输入一个K,K为int范围内的正整数 (保证是两个质数的乘积)
输出
每组测试数据输出一个正整数,表示较大的质数
ac代码:
#include <stdio.h>
#include <stdint.h>
#include <inttypes.h>
int main()
{
uint8_t t;
scanf("%"SCNu8, &t);
for(uint8_t z=0;z<t;z++)
{
uint32_t k;
scanf("%"SCNu32, &k);
for(uint32_t i=2;;i++)
{
if(k%i);
else
{
printf("%"PRIu32"\n", k/i);
goto end;
}
}
end:;
}
return 0;
}
c与编译器、环境无关的整数类型(c99标准)
c语言标准只规定了各种整型的最小范围,却并未给出具体值。
这使得我们对数据类型范围的任何假设都有可能造成不可预知的错误。
所以,c99给出了一系列确定长度的整数类型,如下。
(char其实也是整型)
一、 stdint.h
定义了如下类型,具体什么含义,怎么用,顾名思义。
int8_t int16_t int32_t int64_t
uint8_t uint16_t uint32_t uint64_t
定义了如下宏,具体什么含义,顾名思义。
INTN_MIN, UINTN_MIN, INTN_MAX, UINTN_MAX ;
INT_LEASEN_MIN, INT_LEASEN_MAX ;
INT_FASTN_MIN, INT_FASTN_MAX ;
二、 inttypes.h
注:对c语言来说 “hello” “world” 和 “hello”“world” 和 "helloworld"是等价的,这对理解下面的宏很有必要。
inttypes.h 的例子 64位有符号整数举例
ps:真正头文件中的宏定义比这复杂的多,我这样写只是为了便于理解。
1.遵循gcc标准的系统中,例如debian上的gcc:
头文件中宏定义如下
#define PRId64 "lld"
#define SCNd64 "lld"
使用如下
#include <stdint.h>
int64_t a;
#include <inttypes.h>
scanf("%"SCNd64, &a);
printf("%"PRId64 , a);
printf("%"PRId64"\n", a);
2.vc或windows移植的gcc
头文件中宏定义如下
#define PRId64 "I64d"
#define SCNd64 "I64d"
使用如下
#include <stdint.h>
int64_t a;
#include <inttypes.h>
scanf("%"SCNd64, &a);
printf("%"PRId64 , a);
printf("%"PRId64"\n", a);
辗转相除法

快速幂、快速幂取模
快速幂:
int qpow(int a, int b)//注意:b>=0 !!!
{
int base=a,r=1;
while(b)
{
if(b&1)r *= base;
base *= base;
b=b>>1;
}
return r;
}

快速幂取模:
int qpow_mod(int a, int b, int c)//求 a^b mod c 注意 b>=0 c>0
{
int base = a%c,r=1;
while(b)
{
if(b&1)r= (r*base)%c;
base = (base*base)%c;
b=b>>1;
}
return r;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号