【LeetCode题解】数组Array
1. 数组
直观地看,数组(Array)为一个二元组<index, value>的集合——对于每一个index,都有一个value与之对应。C语言中,以“连续的存储单元”实现数组:
int arr[5], *p_arr[5];
数组提供以\(O(1)\)的复杂度访问元素,下标从0开始。但是,数组的插入、删除操作却非常耗时,因为这涉及到了元素间的移动。
常见的矩阵,可用二维数组表示。二维数组本质上是一个一维数组,其中每个行单元也是一个一维数组,比如,二维数组int x[3][5]的存储结构如下:
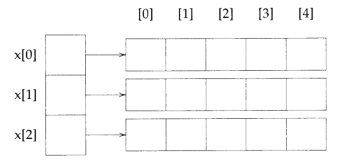
从上图可以看出,x共有4块存储区,一块用于用以存放行单元指针(x[0:2]),另外三块用于存放每一个行单元对应的一维数组。因此,x是一个长度为3的一维数组,而行单元x[0]又是一个长度为5的一维数组。
2. 题解
| LeetCode题目 | 归类 |
|---|---|
| 26. Remove Duplicates from Sorted Array | 删除 |
| 80. Remove Duplicates from Sorted Array II | 删除 |
| 27. Remove Element | 删除 |
| 88. Merge Sorted Array | 合并 |
| 268. Missing Number | 查找 |
| 41. First Missing Positive | 查找 |
| 287. Find the Duplicate Number | 查找 |
| 189. Rotate Array | 旋转 |
| 54. Spiral Matrix | 矩阵遍历 |
| 59. Spiral Matrix II | |
| 48. Rotate Image | 矩阵旋转 |
| 73. Set Matrix Zeroes |
26. Remove Duplicates from Sorted Array
移除数组中重复的元素,由于数据是有序的,所以重复元素一定是相邻的。用两个pointers,一个用于新数组生成,一个用于遍历原数组:
public int removeDuplicates(int[] nums) {
if (nums.length == 0) return 0;
int i = 1;
for (int j = 1; j < nums.length; j++) {
if (nums[j] != nums[i - 1])
nums[i++] = nums[j];
}
return i;
}
80. Remove Duplicates from Sorted Array II
上一问题的变种,新数组中最多允许两个重复元素。
public int removeDuplicates(int[] nums) {
if (nums.length == 0) return 0;
int i = 2;
for (int j = 2; j < nums.length; j++) {
if (nums[j] != nums[i - 2])
nums[i++] = nums[j];
}
return i;
}
27. Remove Element
移去数组中出现的指定元素。也是用两个pointers遍历数组,从头尾两端往中间移动交换:
public int removeElement(int[] nums, int val) {
int i = 0, j = nums.length - 1;
while (i <= j) {
while (j >= i && nums[j] == val) j--; // reduce array size
if (i <= j && nums[i] == val) {
nums[i] = nums[j]; // swap between the current and the last
j--; // reduce array size
}
i++;
}
return j + 1;
}
88. Merge Sorted Array
合并两个有序数组,从后往前开始合并:
public void merge(int[] nums1, int m, int[] nums2, int n) {
int i = m - 1, j = n - 1, k = m + n - 1;
while (j >= 0) {
if (i >= 0 && nums1[i] > nums2[j])
nums1[k--] = nums1[i--];
else
nums1[k--] = nums2[j--];
}
}
268. Missing Number
数的范围[0,n],找出缺失的数。思路:目标和n*(n+1)/2减去数组之和即为缺失数。
public int missingNumber(int[] nums) {
int sum = 0, n = nums.length;
for (int i : nums) {
sum += i;
}
return n * (n + 1) / 2 - sum;
}
41. First Missing Positive
找出缺失的第一个正数,数组的正数范围在[1,n]。将正数i放在i-1位置上,然后找出缺失数。
public int firstMissingPositive(int[] nums) {
for (int i = 0; i < nums.length; i++) {
while (nums[i] > 0 && nums[i] <= nums.length && nums[i] != nums[nums[i] - 1])
swap(nums, i, nums[i] - 1);
}
for (int i = 0; i < nums.length; i++) {
if (nums[i] != i + 1)
return i + 1;
}
return nums.length + 1;
}
private void swap(int[] A, int a, int b) {
int temp = A[a];
A[a] = A[b];
A[b] = temp;
}
287. Find the Duplicate Number
从数组中找出重复数,且数组中的数的范围在[1,n],且只有一个数重复,重复次数>=2。解决思路:将数组看作一个移动链表,按照index=a[index]方式进行移动;那么重复元素会使之成为一个有环的链表,并且重复的元素为环的开始。故可用快慢两个指针来解决。
public int findDuplicate(int[] nums) {
int slow = nums[0], fast = nums[nums[0]];
while (slow != fast) { // find the entry point where slow and fast meet
slow = nums[slow];
fast = nums[nums[fast]];
}
for (fast = 0; slow != fast; ) { // find the entry point where the cycle begins
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
189. Rotate Array
指定一个数组截断点,将左子数组拼接到右子数组后。解决思路:现将整个数组逆序,再将逆序后的左部分逆序、右部分逆序。
public void rotate(int[] nums, int k) {
k %= nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
}
// reverse array from begin to end
private void reverse(int[] a, int begin, int end) {
for (int temp; begin < end; begin++, end--) {
temp = a[begin];
a[begin] = a[end];
a[end] = temp;
}
}
54. Spiral Matrix
二维数组螺旋形遍历。
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> result = new LinkedList<>();
if (matrix.length == 0) return result;
int m = matrix.length, n = matrix[0].length;
for (int start = 0; m - 1 >= 2 * start && n - 1 >= 2 * start; start++) {
int rowEnd = m - start - 1, colEnd = n - start - 1, i, j;
for (j = start; j <= colEnd; j++) // left move
result.add(matrix[start][j]);
if (rowEnd == start) break;
for (i = start + 1; i <= rowEnd; i++) // down move
result.add(matrix[i][colEnd]);
if (colEnd == start) break;
for (j = colEnd - 1; j >= start; j--) // right move
result.add(matrix[rowEnd][j]);
for (i = rowEnd - 1; i > start; i--) // top move
result.add(matrix[i][start]);
}
return result;
}
59. Spiral Matrix II
上一问题的变种,生成螺旋形二维数组。
public int[][] generateMatrix(int n) {
int[][] matrix = new int[n][n];
for (int start = 0, cnt = 1; n - 1 >= 2 * start; start++) {
int end = n - start - 1, i, j;
for (j = start; j <= end; j++, cnt++) // left move
matrix[start][j] = cnt;
if (end == start) break;
for (i = start + 1; i <= end; i++, cnt++) // down move
matrix[i][end] = cnt;
for (j = end - 1; j >= start; j--, cnt++) // right move
matrix[end][j] = cnt;
for (i = end - 1; i > start; i--, cnt++) // top move
matrix[i][start] = cnt;
}
return matrix;
}
48. Rotate Image
顺时针旋转矩阵,相当于每一次把四个对应元素做旋转。
public void rotate(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n / 2; i++) {
for (int j = i; j < n - i - 1; j++) {
int temp = matrix[i][j];
matrix[i][j] = matrix[n - j - 1][i];
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
matrix[j][n - i - 1] = temp;
}
}
}
73. Set Matrix Zeroes
将有0元素的行与列全置为0;用两个set保存这样的行列,然后再置为0——空间复杂度大概为\(O(m+n)\),并非为最优解。
public void setZeroes(int[][] matrix) {
if (matrix.length == 0) return;
int m = matrix.length, n = matrix[0].length;
Set<Integer> rows = new HashSet<>(); // mark rows which contain 0
Set<Integer> columns = new HashSet<>(); // mark columns which contain 0
// phase 1: find zeroes
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == 0) {
rows.add(i);
columns.add(j);
}
}
}
// phase 2: set rows and columns
for (Integer i : rows) {
for (int j = 0; j < n; j++) {
matrix[i][j] = 0;
}
}
for (Integer j : columns) {
for (int i = 0; i < m; i++) {
matrix[i][j] = 0;
}
}
}


