算法提高 12-1三角形
问题描述
为二维空间中的点设计一个结构体,在此基础上为三角形设计一个结构体。分别设计独立的函数计算三角形的周长、面积、中心和重心。输入三个点,输出这三个点构成的三角形的周长、面积、外心和重心。结果保留小数点后2位数字。
样例输出
与上面的样例输入对应的输出。
例:
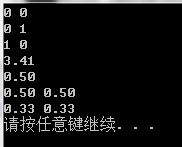
例:
数据规模和约定
输入数据中每一个数的范围。
例:doule型表示数据。
例:doule型表示数据。
这里只对外心的求法做说明,
外心 => 到三个顶点的距离 = 半径
令三顶点分别为 (xa,ya),(xb,yb),(xc,yc)
(x-xa)^2+(y-ya)^2 = (x-xb)^2+(y-yb)^2 = (x-xc)^2+(y-yc)^2
由(x-xa)^2+(y-ya)^2 = (x-xb)^2+(y-yb)^2
=> - 2xa x+xa^2- 2ya y+ya^2 = - 2xb x+xb^2- 2yb y+yb^2
=> 2(xa-xb)x+2(ya-yb)y = xa^2+ya^2-xb^2-yb^2 ---(1)
同理可得 2(xc-xb)x+2(yc-yb)y = xc^2+yc^2-xb^2-yb^2 ---(2)
由行列式值解法(克莱姆法则)可得:
x = △x/△, y = △y/△
其中 △ = 2(xa-xb)(yc-yb) - 2(ya-yb)(xc-xb)
△x = (yc-yb)(xa^2+ya^2-xb^2-yb^2) - (ya-yb)(xc^2+yc^2-xb^2-yb^2)
△y = (xa-xb)(xc^2+yc^2-xb^2-yb^2) - (xc-xb)(xa^2+ya^2-xb^2-yb^2)
令三顶点分别为 (xa,ya),(xb,yb),(xc,yc)
(x-xa)^2+(y-ya)^2 = (x-xb)^2+(y-yb)^2 = (x-xc)^2+(y-yc)^2
由(x-xa)^2+(y-ya)^2 = (x-xb)^2+(y-yb)^2
=> - 2xa x+xa^2- 2ya y+ya^2 = - 2xb x+xb^2- 2yb y+yb^2
=> 2(xa-xb)x+2(ya-yb)y = xa^2+ya^2-xb^2-yb^2 ---(1)
同理可得 2(xc-xb)x+2(yc-yb)y = xc^2+yc^2-xb^2-yb^2 ---(2)
由行列式值解法(克莱姆法则)可得:
x = △x/△, y = △y/△
其中 △ = 2(xa-xb)(yc-yb) - 2(ya-yb)(xc-xb)
△x = (yc-yb)(xa^2+ya^2-xb^2-yb^2) - (ya-yb)(xc^2+yc^2-xb^2-yb^2)
△y = (xa-xb)(xc^2+yc^2-xb^2-yb^2) - (xc-xb)(xa^2+ya^2-xb^2-yb^2)
#include <stdio.h>
#include <math.h>
typedef struct{
double x,y;
}Point;
void Perimeter(Point *p){
printf("%.2lf\n",sqrt((p[1].x - p[0].x)*(p[1].x - p[0].x)+(p[1].y - p[0].y)*(p[1].y - p[0].y))+
sqrt((p[2].x - p[0].x)*(p[2].x - p[0].x)+(p[2].y - p[0].y)*(p[2].y - p[0].y)) +
sqrt((p[2].x - p[1].x)*(p[2].x - p[1].x)+(p[2].y - p[1].y)*(p[2].y - p[1].y)));
}
void Area(Point *p){
//海伦公式sqrt(p(p-a)(p-b)(p-c))or向量法
//这里采用向量法
Point p1[2];
double cos_theta,sin_theta,model1,model2;
p1[0].x = p[1].x - p[0].x,p1[0].y = p[1].y - p[0].y;
p1[1].x = p[2].x - p[0].x,p1[1].y = p[2].y - p[0].y;
model1 = sqrt((p[1].x - p[0].x)*(p[1].x - p[0].x)+(p[1].y - p[0].y)*(p[1].y - p[0].y));
model2 = sqrt((p[2].x - p[0].x)*(p[2].x - p[0].x)+(p[2].y - p[0].y)*(p[2].y - p[0].y));
cos_theta = (p1[0].x * p1[1].x + p1[0].y * p1[1].y)/(model1*model2);
sin_theta = sqrt(1-cos_theta*cos_theta);
printf("%.2lf\n",0.5*model1*model2*sin_theta);
}
void Circumcenter(Point *p){
//外接圆,圆心到三个顶点的距离相等列方程,可解出(x,y)
double denominator,delta_x,delta_y;
denominator = 2*(p[1].x - p[0].x)*(p[2].y - p[0].y) - 2*(p[1].y - p[0].y)*(p[2].x - p[0].x);
delta_x = (p[2].y - p[0].y)*(p[1].x*p[1].x + p[1].y*p[1].y - p[0].x*p[0].x - p[0].y*p[0].y)
-(p[1].y - p[0].y)*(p[2].x*p[2].x + p[2].y*p[2].y - p[0].x*p[0].x - p[0].y*p[0].y);
delta_y = (p[1].x - p[0].x)*(p[2].x*p[2].x + p[2].y*p[2].y - p[0].x*p[0].x - p[0].y*p[0].y)
-(p[2].x - p[0].x)*(p[1].x*p[1].x + p[1].y*p[1].y - p[0].x*p[0].x - p[0].y*p[0].y);
printf("%.2lf %.2lf\n",delta_x/denominator,delta_y/denominator);
}
void Center_Of_Gravity(Point *p) {
//一个顶点到另一边的中心连线的2/3处
Point p1;
p1.x = (p[0].x + p[1].x)/2.0,p1.y = (p[0].y + p[1].y)/2.0;
printf("%.2lf %.2lf\n",p[2].x+2.0*(p1.x - p[2].x)/3,p[2].y+2.0*(p1.y - p[2].y)/3);//注意哪个减去哪个
}
int main(){
Point p[3];
int i;
for(i = 0; i < 3; i ++)
scanf("%lf%lf",&p[i].x,&p[i].y);
Perimeter(p);
Area(p);
Circumcenter(p);
Center_Of_Gravity(p);
return 0;
}
有关外心的解法来自:http://www.zybang.com/question/28231e30758cfa6af7567f1482011fd9.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号