拟阵交 [Deltix Round, Summer 2021 H DIY Tree 题解]

拟阵、拟阵交

在此忽略所有理论证明，只保留能够应用拟阵的最少的概念。

定义 [拟阵]

给定集合 \(U\)，\(\mathcal{F}\) 是 \(U\) 中一些子集的集合，即 \(\mathcal{F} \subseteq 2^{U}\)，称 \(\mathcal{M}=(U,\mathcal{F})\) 为拟阵，当且仅当其满足：
(1) \(\emptyset \in \mathcal{F}\)
(2) （遗传性）\(A \in \mathcal{F}, B \subseteq A \Rightarrow B \in \mathcal{F}\)
(3) （交换性）\(A, B \in \mathcal{F}, |A| < |B| \Rightarrow \exists\ b\in B-A. A \cup \left\{ b \right\} \in \mathcal{F}\)
其中 \(\mathcal{F}\) 内的元素被称为独立集。

定义 [基，环]

\(\mathcal{F}\) 中的极大独立集称为拟阵 \(\mathcal{M}\) 的一个基。
\(\mathcal{F}\) 中的极小非独立集称为拟阵 \(\mathcal{M}\) 的一个环。

问题 [最小带权基]

给 \(U\) 的每个元素 \(e\) 赋予一个权值 \(w(e)\)，即给定一个权值函数 \(w:U\rightarrow \mathbb{Z}\)。
给定拟阵 \(\mathcal{M}=(U,\mathcal{F})\)，求 \(\mathcal{M}\) 的一组最小带权基。

Kruskal 算法

所有元素按权从小到大排序，\(U=\{e_1,e_2,...,e_n\}\)。

初始解集 \(S = \emptyset\)
循环 \(i=1:n\)，如果 \(S \cup \{e_i\}\) 是独立集，令 \(S\leftarrow S\cup \{e_i\}\)。
输出 \(S\)

（这不就是最小生成树吗？）

2-拟阵交问题

设 \(\mathcal{M}_1=(U,\mathcal{F}_1), \mathcal{M}_2=(U,\mathcal{F}_2)\) 是 \(U\) 上的两个拟阵，令它们的交为 \(\mathcal{I}=(U, \mathcal{F}_1 \cap \mathcal{F}_2)\)。
一般来说，\(\mathcal{I}\) 并不是拟阵，因此不能使用 Kruskal 算法来求解 \(\mathcal{I}\) 上的公共极大独立集问题。
但2-拟阵交问题是存在多项式算法的，该算法依赖于一个有向二分图，又称为交换图。
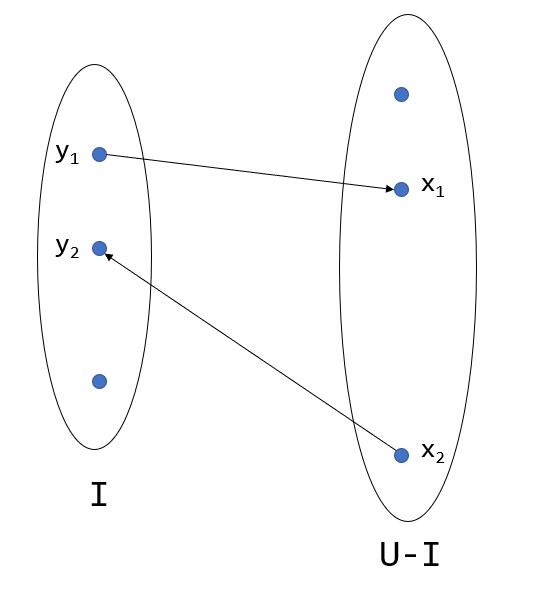
给定一个集合 \(I \in \mathcal{F}_1 \cap \mathcal{F}_2\)，它的交换图 \(G_{\mathcal{M}_1, \mathcal{M}_2}(I)\) 是所有 \(U\) 的元素为点集的一个二分图。其中 \(I\) 在二分图的一侧，\(U-I\) 在另一侧。
\(I\) 中元素 \(y_1\) 指向 \(U-I\) 中元素 \(x_1\) 当且仅当 \((I-\{y_1\})\cup \{x_1\} \in \mathcal{F}_1\)，即 \(I\) 去掉 \(y_1\) 再增加 \(x_1\) 后，仍然是 \(\mathcal{M}_1\) 中的一个独立集。
\(U-I\) 中元素 \(x_2\) 指向 \(I\) 中元素 \(y_2\) 当且仅当 \((I-\{y_2\})\cup \{x_2\} \in \mathcal{F}_2\)，即 \(I\) 去掉 \(y_2\) 再增加 \(x_2\) 后，仍然是 \(\mathcal{M}_2\) 中的一个独立集。

2-拟阵交算法

初始解集 \(I = \emptyset\)
循环
2.1. 构建交换图 \(G_{\mathcal{M}_1, \mathcal{M}_2}(I)\)
2.2. 令 \(X_1 := \left\{ e\in U-I | I\cup\{e\} \in \mathcal{F}_1 \right\}\)
令 \(X_2 := \left\{ e\in U-I | I\cup\{e\} \in \mathcal{F}_2 \right\}\)
2.3. 计算交换图 \(G_{\mathcal{M}_1, \mathcal{M}_2}(I)\) 上点集 \(X_1\) 到 \(X_2\) 的最短路 \(P\)
2.4. \(I\leftarrow I \Delta P\) ( \(\Delta\) 为对称差）
直到 \(P\) 不存在，输出 \(I\)

假设判定是否为独立集的复杂度是\(O(1)\)，令 \(n=|U|\)，\(r=\min\{r(\mathcal{M}_1), r(\mathcal{M}_2)\}\)，（\(r(\mathcal{M})\) 是拟阵 \(\mathcal{M}\) 的极大独立集的大小，也称为它的秩）。由于循环最多进行 \(r\) 次，每次 BFS 的复杂度是 \(O(rn)\)，因此复杂度为 \(O(r^2n)\)。

如果希望求最小权的最大公共独立集，只需要给交换图 \(G_{\mathcal{M}_1, \mathcal{M}_2}(I)\) 的每个点定义权重

\[ f(e) = \left\{ \begin{array} \ -w(e), e \in I \\ w(e), e \in U - I \end{array} \right. \]

然后把 BFS 换成 Bellman-Ford 算法，求 \(X_1\) 到 \(X_2\) 的最短路（第一关键字是点权最小，第二关键字是边数最少）即可。（此时复杂度是 \(O(r^3n)\)，但由于Bellman-Ford跑不满，所以...）

k-拟阵交问题（\(k\geq 3\)）

很可惜，这是 NP-complete 的

Deltix Round, Summer 2021 H DIY Tree

链接
给定 \(n(\leq 50)\) 个点的无向完全图，求满足前 \(k(\leq 5)\) 个点中，第 \(i\) 个点的度数不超过 \(d_i\) 的最小生成树

做法

首先对于后面的 \(n-k\) 个点的团中的 \(\frac{(n-k)(n-k-1)}{2}\) 条边中，只有 \(n-k-1\) 条边是有可能成为答案的，这部分可以通过一次最小生成树预处理得到。
之后枚举前面的 \(k\) 个点的团中 \(\frac{k(k-1)}{2}\) 条边形成的所有森林（这样的森林并不会很多）。
定义集合 \(U = \{前k个点与后n-k个点之间的边\} \cup \{ 后n-k个点中有用的 n-k-1 条边\}\)，要从这个集合中得到既符合度数要求，又无环的权值最小的一组边。

定义两个拟阵 \(\mathcal{M}_1=(U,\mathcal{F}_1), \mathcal{M}_2=(U,\mathcal{F}_2)\) ，其中
\(U\) 的子集 \(A \in \mathcal{F}_1\) 当且仅当 \(A\) 满足度数要求；
\(U\) 的子集 \(B \in \mathcal{F}_2\) 当且仅当 \(B\) 无环。

为了证明它们是拟阵，空集和遗传性都是显然的，只有交换性需要证明。
对于 \(\mathcal{M}_1\)，如果 \(A, A'\) 都满足度数要求，且 \(|A|<|A'|\)，如果 \(A'-A\) 中存在 \(\{ 后n-k个点中有用的 n-k-1 条边\}\) 里的元素 \(e\)，\(A+\{e\}\) 是不会破坏度数要求的。如果不存在这样的元素，说明前 \(k\) 个点中有至少1个点，\(A'\) 的度数比 \(A\) 大，把这个点连着的某条边 \(e\) 给 \(A\) 即可。因此 \(\mathcal{M}_1\) 是满足交换性要求的，所以是 \(U\) 上的一个拟阵。
对于 \(\mathcal{M}_2\)，它其实是一个图拟阵（图拟阵就是图中所有生成树的集合）。

那么问题就转化为，枚举所有前 \(k\) 个点的森林，每次求最小权拟阵交，假设森林数是 \(N\)，则复杂度是 \(O(Nkn^4)\)。

思考

为什么需要枚举前 \(k\) 个点的森林，而不能直接让 \(U=\{前k个点的所有边\} \cup \{后n-k个点中有用的n-k-1条边\}\)，然后只做一次拟阵交呢？

代码（很丑的实现）

#include <bits/stdc++.h>
using namespace std;

const int maxn = 55;

int w[maxn][maxn], d[maxn];
struct edge {
    int u, v, w;
    bool operator < (const edge & a) const {
        return w < a.w;
    }
};

struct node {
    int to, w, nex;
} buf[maxn * 2];
int h[maxn], buf_tot;
void add_edge(int u, int v, int w) {
    buf[++buf_tot] = (node){v, w, h[u]};
    h[u] = buf_tot;
}

struct node2 {
    int to, nex;
} buf2[maxn * maxn * 12];
int h2[maxn * 6], buf2_tot;
void add_edge2(int u, int v) {
    buf2[++buf2_tot] = (node2){v, h2[u]};
    h2[u] = buf2_tot;
}

int I[maxn * 6];
int pre[maxn], pre_id[maxn], rt[maxn], dep[maxn], deg[maxn];
void dfs(int u, int p, int r) {
    rt[u] = r;
    for (int i=h[u]; i; i=buf[i].nex) {
        int v = buf[i].to;
        if (v == p) continue;
        pre[v] = u;
        pre_id[v] = buf[i].w;
        dep[v] = dep[u] + 1;
        dfs(v, u, r);
    }
}

int pa[maxn];
int fnd(int u) {
    return u == pa[u] ? u : (pa[u] = fnd(pa[u]));
}

int X2[maxn * 6], dis_w[maxn * 6], dis_num[maxn * 6], dis_pre[maxn * 6];
int vis[maxn * 6], cnt[maxn * 6];

int main(void) {

    int n, k; scanf("%d%d", &n, &k);
    for (int i=1; i<=k; i++) scanf("%d", &d[i]);
    for (int i=1; i<=n; i++) {
        for (int j=i+1; j<=n; j++) scanf("%d", &w[i][j]);
    }

    for (int i=k+1; i<=n; i++) d[i] = n;

    for (int i=k+1; i<=n; i++) pa[i] = i;
    vector <edge> e;
    for (int i=k+1; i<=n; i++) for (int j=i+1; j<=n; j++) e.push_back((edge){i, j, w[i][j]});
    sort(e.begin(), e.end());

    vector <edge> U;
    for (int i=0; i<(int)e.size(); i++) {
        int u = fnd(e[i].u), v = fnd(e[i].v);
        if (u == v) continue;
        U.push_back(e[i]);
        pa[u] = v;
    }

    for (int i=1; i<=k; i++) {
        for (int j=k+1; j<=n; j++) U.push_back((edge){i, j, w[i][j]});
    }

    vector <edge> V;
    for (int i=1; i<=k; i++) {
        for (int j=i+1; j<=k; j++) V.push_back((edge){i, j, w[i][j]});
    }

    int ans = (int)1e9;

    for (int sv=0, sz=(1<<V.size()); sv<sz; sv++) {
        for (int i=1; i<=k; i++) pa[i] = i;
        for (int i=1; i<=n; i++) deg[i] = 0;
        int ok = 1;
        for (int j=0; j<(int)V.size(); j++) if ((sv>>j) & 1) {
            int u = fnd(V[j].u), v = fnd(V[j].v);
            if (u == v) { ok = 0; break; }
            pa[u] = v;
            deg[V[j].u]++, deg[V[j].v]++;
        }
        for (int i=1; i<=k; i++) if (deg[i] > d[i]) ok = 0;
        if (!ok) continue;

        for (int i=0; i<U.size(); i++) I[i] = 0;

        // M1 : deg(i) <= d(i)
        // M2 : no circle
        while (1) {
            // for checking if (I - {y}) U {x} \in M2
            buf_tot = 0;
            for (int i=1; i<=n; i++) h[i] = pre[i] = pre_id[i] = dep[i] = rt[i] = 0;
            for (int j=0; j<(int)V.size(); j++) if ((sv>>j) & 1) {
                int u = V[j].u, v = V[j].v;
                add_edge(u, v, -1);
                add_edge(v, u, -1);
            }
            for (int j=0; j<(int)U.size(); j++) if (I[j]) {
                int u = U[j].u, v = U[j].v;
                add_edge(u, v, j);
                add_edge(v, u, j);
            }
            for (int i=1; i<=n; i++) if (pre[i] == 0) dfs(i, 0, i);

            buf2_tot = 0;
            for (int i=0; i<(int)U.size(); i++) h2[i] = 0;

            // a -> b : I - {a} U {b} \in M1
            vector <int> IP;
            for (int a=0; a<(int)U.size(); a++) if (I[a]) {
                IP.push_back(a);
                for (int b=0; b<(int)U.size(); b++) if (!I[b]) {
                    deg[U[a].u]--, deg[U[a].v]--;
                    deg[U[b].u]++, deg[U[b].v]++;
                    if (deg[U[b].u] <= d[U[b].u] && deg[U[b].v] <= d[U[b].v]) {
                        add_edge2(a, b);
                    }
                    deg[U[a].u]++, deg[U[a].v]++;
                    deg[U[b].u]--, deg[U[b].v]--;
                }
            }

            // b -> a : I - {b} U {a} \in M2
            for (int b=0; b<(int)U.size(); b++) if (!I[b]) {
                int u = U[b].u, v = U[b].v;
                if (rt[u] != rt[v]) {
                    for (auto a : IP) {
                        add_edge2(b, a);
                    }
                } else {
                    while (u != v) {
                        if (dep[u] > dep[v]) {
                            if (~pre_id[u]) add_edge2(b, pre_id[u]);
                            u = pre[u];
                        } else {
                            if (~pre_id[v]) add_edge2(b, pre_id[v]);
                            v = pre[v];
                        }
                    }
                }
            }

            // X1 := { e \in U - I | I + {e} \in M1 }
            // X2 := { e \in U - I | I + {e} \in M2 }
            for (int e=0; e<U.size(); e++) {
                dis_w[e] = (int)1e9;
                dis_num[e] = 0;
                dis_pre[e] = -1;
                vis[e] = 0;
                cnt[e] = 0;
            }

            queue <int> Q;

            for (int i=0; i<U.size(); i++) X2[i] = 0;
            for (int e=0; e<U.size(); e++) if (!I[e]) {
                if (deg[U[e].u] + 1 <= d[U[e].u] && deg[U[e].v] + 1 <= d[U[e].v]) {
                    Q.push(e);
                    cnt[e]++;
                    dis_w[e] = U[e].w, dis_num[e] = 0;
                }
                if (rt[U[e].u] != rt[U[e].v]) X2[e] = 1;
            }

            while (!Q.empty()) {
                int e = Q.front(); Q.pop();
                vis[e] = false;
                for (int i=h2[e]; i; i=buf2[i].nex) {
                    int v = buf2[i].to;
                    int w = I[v] ? -U[v].w : U[v].w;
                    if (dis_w[v] > dis_w[e] + w
                        || (dis_w[v] == dis_w[e] + w && dis_num[v] > dis_num[e] + 1)) {
                        dis_w[v] = dis_w[e] + w;
                        dis_num[v] = dis_num[e] + 1;
                        dis_pre[v] = e;
                        if (!vis[v]) {
                            vis[v] = true;
                            Q.push(v);
                            if (++cnt[v] > U.size()) {
                                // should not have negative loops
                                assert(0);
                            }
                        }
                    }
                }
            }

            int e = -1, min_dis = (int)1e9, min_num = 0;
            for (int i=0; i<U.size(); i++) if (X2[i]) {
                if (dis_w[i] < min_dis || (dis_w[i] == min_dis && dis_num[i] < min_num)) {
                    e = i;
                    min_dis = dis_w[i], min_num = dis_num[i];
                }
            }

            if (min_dis == (int)1e9) break;

            while (~e) {
                if (I[e]) deg[U[e].u]--, deg[U[e].v]--;
                else deg[U[e].u]++, deg[U[e].v]++;
                I[e] ^= 1;
                e = dis_pre[e];
            }

        }


        for (int i=1; i<=n; i++) pa[i] = i, deg[i] = 0;

        int cnt = 0, tmp = 0;
        for (int j=0; j<V.size(); j++) if ((sv>>j) & 1) {
            int u = fnd(V[j].u), v = fnd(V[j].v);
            assert(u != v);
            pa[u] = v;
            deg[V[j].u]++, deg[V[j].v]++;
            tmp += V[j].w;
            cnt++;
        }
        for (int j=0; j<U.size(); j++) if (I[j]) {
            int u = fnd(U[j].u), v = fnd(U[j].v);
            assert(u != v);
            pa[u] = v;
            deg[U[j].u]++, deg[U[j].v]++;
            tmp += U[j].w;
            cnt++;
        }

        if (cnt < n - 1) continue;

        for (int i=1; i<=n; i++) assert(fnd(i) == fnd(1));
        for (int i=1; i<=n; i++) assert(deg[i] <= d[i]);

        ans = min(ans, tmp);
    }

    printf("%d\n", ans);

    return 0;
}

参考文献

《浅谈拟阵的一些拓展及其应用》杨乾澜
拟阵及应用（四）

posted @ 2021-09-01 22:04 emofunc 阅读(134) 评论(0) 编辑收藏举报

刷新页面返回顶部

emofunc