Beatty序列与Wythoff博弈

Beatty序列

定义1

一个正无理数\(r\)生成的Beatty序列是指这样的一个序列，

\[\mathcal{B}_r= \left( \lfloor ri\rfloor \right)_{i\geq 1} \]

定理2 Rayleigh定理 (Beatty定理)

假设正无理数 \(r>1\)，\(s\) 满足 \(\frac{1}{r}+\frac{1}{s}=1\)，则 \(\mathcal{B}_r\) 与 \(\mathcal{B}_s\) 是全体正整数的一个分割。即任意一个正整数存在且仅存在于 \(\mathcal{B}_r\) 和 \(\mathcal{B}_s\) 的其中一个序列。

举个例子，\(r=\sqrt{2}, s=2+\sqrt{2}\) 时，这两个序列为

n	1	2	3	4	5	6	7	8	9	10	11	...
\(\mathcal{B}_r\)	1	2	4	5	7	8	9	11	12	14	15	...
\(\mathcal{B}_s\)	3	6	10	13	17	20	23	27	30	34	37	...

证明

考虑所有 \(\frac{j}{r}\ (j\geq 1)\) 和 \(\frac{k}{s}\ (k\geq 1)\) 排成的非递减序列。
首先该序列中的数两两不同，否则假设 \(\frac{j}{r}=\frac{k}{s}\)，那么将会得到 \(\frac{r}{s}=r-1=\frac{j}{k}\)，左边是无理数，右边是有理数，矛盾。
然后考虑 \(\frac{j}{r}\) 在该序列(1-index)中的位置，在 \(\frac{i}{r}\) 里面有 \(j\) 个不大于 \(\frac{j}{r}\)，在 \(\frac{i}{s}\) 里面有 \(\lfloor \frac{js}{r} \rfloor\) 个不大于 \(\frac{j}{r}\)，所以 \(\frac{j}{r}\) 在序列中的位置是

\[j+\lfloor \frac{js}{r} \rfloor=j+\lfloor j(s-1)\rfloor=\lfloor js \rfloor \]

而 \(\frac{k}{s}\) 在序列中的位置是

\[k+\lfloor \frac{kr}{s} \rfloor=k+\lfloor k(r-1)\rfloor=\lfloor kr \rfloor \]

由于该序列中的数两两不同，所以 \(\{ \lfloor js\rfloor \}\) 和 \(\{ \lfloor kr\rfloor \}\) 必然是正整数的一个分割。

这个定理就是核心了，但是为了之后叙述方便，在这里再补充一个小结论。

推论3

假设正无理数 \(1<r<s\) 且 \(1/r+1/s=1\)，有

\[(\mathcal{B}_r)_i = \operatorname{mex}\left\{ 0, (\mathcal{B}_r)_j, (\mathcal{B}_s)_j | j < i \right\} \]

这里 \(\operatorname{mex}S\) 指的是取最小的没有在集合 \(S\) 中出现的非负整数。

证明

因为 \(\mathcal{B}_r\) 和 \(\mathcal{B}_s\) 都是递增的，所以有 \((\mathcal{B}_r)_i < (\mathcal{B}_r)_k, (k>i)\) 和 \((\mathcal{B}_r)_i < (\mathcal{B}_s)_k, (k\geq i)\)。简而言之就是后面的数都比 \((\mathcal{B}_r)_i\) 要大。
假设 \(x=\operatorname{mex}\left\{ 0, (\mathcal{B}_r)_j, (\mathcal{B}_s)_j | j < i \right\}\) 是最小的之前所有数中没出现的正整数。如果 \((\mathcal{B}_r)_i>x\)，那 \(x\) 将永远不能出现这两个序列中，这和定理2矛盾。

Wythoff博弈

Wythoff博弈的玩法是，有两堆石子，石子数分别为 \(n,m\)。两个玩家轮流进行，轮到一方的时候，该玩家可以做

• 从其中一堆石子中取走 \(x>1\) 个（\(x\) 不能超过该堆的石子数）；或
• 从两堆石子中同时取走 \(x>1\) 个（\(x\) 不能超过任意一堆的石子数）。

如果轮到某方的时候，玩家无法操作，则该玩家输。

打表观察一下N态（必胜态）和P态（必败态）的规律。

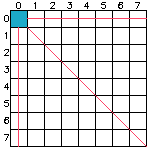
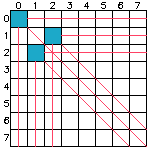
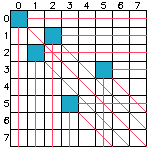
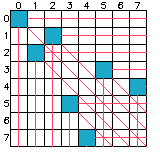
上图蓝色块为P态，其余为N态。打表的流程就是从(0,0)出发，(0,0)是P态，那么其往下、往右、往右下的三条线都是N态（因为它们都可以走到(0,0)这个P态）。然后再选择最靠左上的不是N态的格子(1,2)和(2,1)，如此重复。最终得到的图如

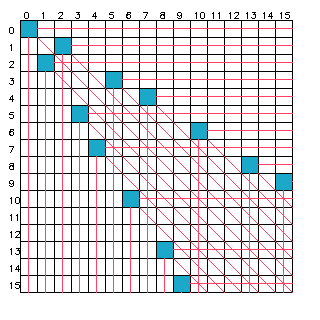
由于图中 \(n,m\) 是对称的，不妨只考虑 \(n<m\)，把所有P态按 \(n\) 从小到大列出 \((n,m)\) 为

\[(0,0),(1,2),(3,5),(4,7),... \]

写成两行，用 \(a=(a_i)_{i\geq 1}\) 和 \(b=(b_i)_{i\geq 1}\) 分别代表对应的 \(n\) 和 \(m\)，得到

\(i\)	0	1	2	3	4	5	6	7	8	9	10	11	...
\(a_i\)	0	1	3	4	6	8	9	11	12	14	16	17	...
\(b_i\)	0	2	5	7	10	13	15	18	20	23	26	28	...

定理5

\(a\) 和 \(b\) 满足递推关系

\[a_i=\operatorname{mex}\left\{a_j, b_j| j<i \right\} \]

\[b_i=a_i+i \]

证明

其实我们的图就是这样做出来的嘛...
归纳法。
\((a_0, b_0)=(0,0)\)。
假设所有 \((a_j,b_j), (j<i)\) 都满足定理5的递推关系。
令 \(x=\operatorname{mex}\left\{a_j, b_j| j<i \right\}\)，我们证明下一个P态正是 \((x,x+i)\)。
首先，下一个P态 \((n,m)\)，不可能 \(n<x\)，否则 \((n,m)\) 能走到某个之前的P态，或者某个之前的P态能走到 \((n,m)\)。
其次，下一个P态不可能是 \((x,x+j),(j<i)\)，因为根据归纳假设已经存在 \((a_j,a_j+j)\) 为P态，这仍然导致一个P态能到达另一个P态，矛盾。
最后，\((x,x+i)\)确实是P态，因为它无法走到任意一个已经存在的P态。所以\((a_i,b_i)=(x,x+i)\)。

终于到了这一步，看起来上面的式子已经很简洁了，但是Wythoff还发现了更简洁的表述

定理6

\[a_i=\lfloor \phi i\rfloor \]

\[b_i=\lfloor \phi^2 i\rfloor \]

其中，\(\phi=\frac{1+\sqrt{5}}{2}\) 是黄金分割比。

证明

我们构造两个互补的Beatty序列 \(\mathcal{B}_r\)、\(\mathcal{B}_s\)，使得这两个序列符合定理5的递推关系。由于需要满足 \(b_i=a_i+i\)，所以令 \(s=r+1\)，联合 \(\frac{1}{r}+\frac{1}{s}=1\)，得到 \(r^2 - r - 1 = 0\)。舍去小于1的根，得到

\[r=\frac{1+\sqrt{5}}{2}=\phi \]

\[s=\frac{3+\sqrt{5}}{2}=\phi^2 \]

根据推论3，这两个序列确实满足 \((\mathcal{B}_r)_i = \operatorname{mex}\left\{ 0, (\mathcal{B}_r)_j, (\mathcal{B}_s)_j | j < i \right\}\)，而且

\[(\mathcal{B}_s)_i = \lfloor si \rfloor = \lfloor (r+1)i \rfloor = \lfloor ri \rfloor + i = (\mathcal{B}_r)_i + i \]

因此 \(\mathcal{B}_r\)、\(\mathcal{B}_s\) 符合定理5的递推关系，补充定义 \((\mathcal{B}_r)_0=(\mathcal{B}_s)_0 = 0\)，由归纳法即可得到 \(a=\mathcal{B}_r\)，\(b=\mathcal{B}_s\)。

扩展：k-Wythoff博弈

k-Wythoff博弈是Wythoff博弈的推广，其和Wythoff博弈唯一的区别是轮到某个玩家时，玩家可以：

• 从其中一堆石子中取走 \(x>1\) 个；或
• 从两堆石子中分别取走 \(x>1,y>1\) 个，满足 \(|x-y|\leq k\)。

显然Wythoff博弈可以看成 \(k=0\) 时的k-Wythoff博弈。

按照同样的方式，可以类似得到k-Wythoff博弈的 PN态表 和 \(a,b\)序列，以下给出 \(k=1\) 时候的表和序列

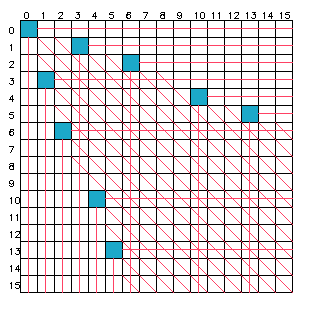
\(i\)	0	1	2	3	4	5	6	7	8	9	10	11	...
\(a_i\)	0	1	2	4	5	7	8	9	11	12	14	15	...
\(b_i\)	0	3	6	10	13	17	20	23	27	30	34	37	...

(这刚好就是上面的 \(\mathcal{B}_{\sqrt{2}}\) 和 \(\mathcal{B}_{2+\sqrt{2}}\)，太神奇啦，不是。)

命题7

\(a\) 和 \(b\) 满足递推关系

\[a_i=\operatorname{mex}\left\{a_j, b_j| j<i \right\} \]

\[b_i=a_i+(k+1)i \]

命题8

\[a_i=\lfloor ri \rfloor \]

\[b_i=\lfloor s i\rfloor \]

其中，\(r=\frac{\sqrt{k^2+2k+5}+1-k}{2}\)，\(s=\frac{\sqrt{k^2+2k+5}+3+k}{2}\)。

这两个命题都是类似的就能证完，自证不难。

题目

hdu 1527 (Wythoff博弈)
hdu 2177 (Wythoff博弈)
hdu 6869 (k-Wythoff博弈)
nowcoder (k-Wythoff博弈)

小结

这个东西一直不会...最近终于补了，好像还有一些神奇的推广，但暂时找不到题目，就先假装不存在吧（逃）

参考文献

https://en.wikipedia.org/wiki/Beatty_sequence
https://en.wikipedia.org/wiki/Wythoff's_game
http://www.wisdom.weizmann.ac.il/~fraenkel/Papers/WythoffWisdomJune62016.pdf