最大堆max-heap最小堆min-heap
heap概述
堆（Heap)是计算机科学中一类特殊的数据结构的统称，堆通常是一个可以被看做一棵树的数组对象。
1、堆是一棵完全二叉树；
2、堆中的某个结点的值总是大于等于（最大堆）或小于等于（最小堆）其孩子结点的值。
3、堆中每个结点的子树都是堆树。
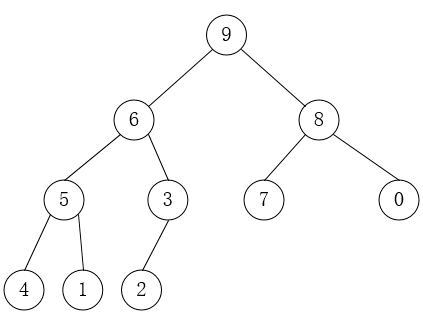
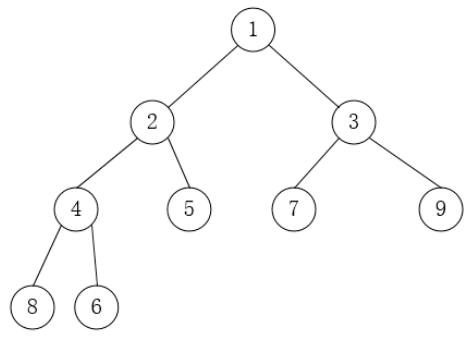
最大堆max-heap：每个节点的键值（key）都大于或等于其子节点键值
最小堆min-heap：每个节点的键值（key）都小于或等于其子节点键值
完全二叉树整棵树内没有任何节点漏洞，这带来一个好处：我们可以利用array来存储所有节点。假设我们动用一个小技巧，将array的#0元素保留（或设为无限大值或无限小值），那么完全二叉树中的某个节点位于array的i处时，其左子节点位于array的2i处，其右子节点位于array的2i+1处，其父节点位于“i/2"。
注：完全二叉树：若二叉树的深度为h，则除第h层外，其他层的结点全部达到最大值，且第h层的所有结点都集中在左子树。
heap算法
堆通常是一个可以被看做一棵树的数组对象，所以它的结构就并不是左指针和右指针了，而是以数组的形式，而且为了方便后面的操作（像插入、删除...），堆的结构中还有Size代表它当前的长度和Capacity代表它的总容量：
struct MaxHeap { EType *heap; //存放数据的空间，下标从1开始存储数据，下标为0的作为工作空间，存储临时数据。 int MaxSize; //MaxSize是存放数据元素空间的大小 int HeapSize; //HeapSize是数据元素的个数 }; MaxHeap H;
1、构造最大堆
基本思想：首先将每个叶子结点视为一个堆，再将每个叶子结点于其父节点一起构成一个包含更多结点的堆。所以在构造堆的时候，首先需要找到最后一个结点的父节点，从这个节点开始构造最大堆，直到该节点前面的所有分支节点都处理完毕。
注意： 在二叉树中，若当前节点的下标为 i， 则其父节点的下标为 i/2，其左子节点的下标为 i*2，其右子节点的下标为i*2+1；
2、初始化堆
void MaxHeapInit(MaxHeap &H) { for(int i=H.HeapSize/2;i>=1;i--) { H.heap[0]=H.heap[i]; int son=i*2; while(son<H.HeapSize) { if(son<H.HeapSize&&H.heap[son]<H.heap[son+1]) son++; if(H.heap[i]>H.heap[son]) break; else if(son<H.heapSize&&H.heap[son]>H.heap[son+1] { H.heap[son/2]=H.heap[son]; son*=2; } } H.heap[son/2]=H.heap[0]; } }
3、最大堆中插入节点
最大堆中插入节点，先在堆末尾插入该节点，然后按照堆的初始化过程将该节点放入到合适的位置。
void MaxHeapInsert(MaxHeap &H, EType &x) { if(H.HeapSize==H.MaxSize) return false; int i=++H.HeapSize; while(i!=1&&x>H.heap[i/2]) { H.heap[i]=H.heap[i/2]; i/=2; } H.heap[i]=x; return true; }
4、最大堆删除节点
将最大堆的最后一个节点放到根节点，然后删除最大值，然后再把新的根节点放到合适的位置。
void MaxHeapDelete(MaxHeap &H, EType &x) { if(H.HeapSize==0) return false; x=H.heap[1]; H.heap[0]=H.heap[H.HeapSize--]; int i=1, son=i*2; while(son<H.HeapSize) { if(son<H.HeapSize&&H.heap[son]<H.heap[son+1]) son++; if(H.heap[i]>H.heap[son]) break; H.heao[i]=H.heap[son]; i=son; son*=2; } H.heap[i]=H.heap[0]; return true; }
5、堆排序
#include<iostream> using namespace std; void swap(int &a, int &b) { int temp=a; a=b; b=temp; } void quick_build(int a[], int len, int root) { int left=root*2+1; int flag=left; while(left<len) { int right=left+1; while(right<len&&a[right]>a[left]) flag=right; } if(a[root]<a[flag]) { swap(a[root],a[flag]); heap_build(a,len,flag); } void quick_sort(int a[], int len) { for(int i=len/2;i>0;i--) heap_build(a,len, i); for(int j=len-1;j>0;j--) { swap(a[0],a[j]); heap_build(a,0,j); } }
参考：
