正则化

正则化

https://www.sohu.com/a/285178444_654419

过拟合肯定不是我们想要的结果，因此需要使用一些方法来尽量避免过拟合的发生。比如常见的过拟合处理方法有：

• 增加数据量
• 简化模型
• 交叉验证
• 正则化

 

 

如果我们的模型过度地学习并拟合了数据，那么就会连一些噪音数据也一起学习（上图中比较复杂的曲线）。但事实上数据在一定范围内是随机的，我们无法预知未知数据长什么样，而且它在很大概率上也不会和训练数据一模一样，因此如果过分地的学习就会导致模型缺少泛化能力，即过拟合。

如何判断一个结果是否发生了过拟合现象呢？

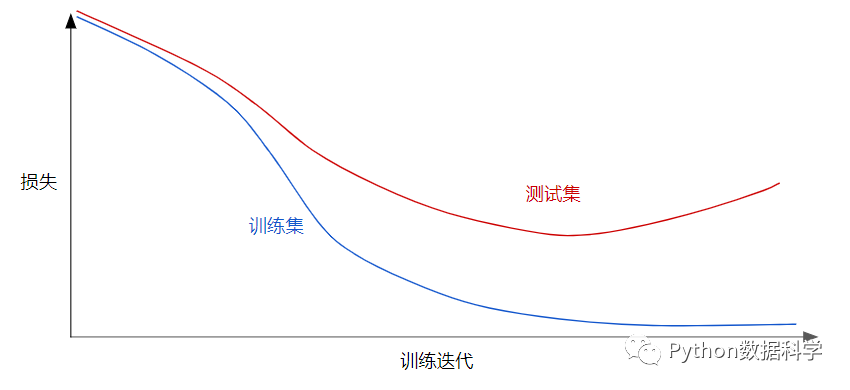
如上图迭代次数的增加，训练集和测试集的损失逐渐有越来越大的差距，这就表明发生了过拟合。

过拟合肯定不是我们想要的结果，因此需要使用一些方法来尽量避免过拟合的发生。比如常见的过拟合处理方法有：

• 增加数据量
• 简化模型
• 交叉验证
• 正则化
• ...

下面就来说说正则化，一种用来避免过拟合的好方法。

▍

▍什么是正则化？

 

正则化就是通过对模型参数进行调整（数量和大小），降低模型的复杂度，以达到可以避免过拟合的效果。正则化是机器学习中的一种叫法，其它领域内叫法各不相同：

 

机器学习把L1和L2叫正则化，统计学领域叫惩罚项，数学领域叫范数。

 

如果不加入正则化，我们的目标是最小化损失函数，即经验风险最小化：

 

 

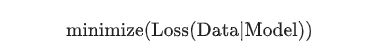
加入正则化以后，不再是最小化损失函数了，而是变成以最小化损失和复杂度为目标了，这个称为结构风险最小化：

 

 

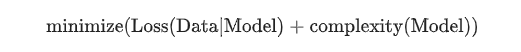
现在，我们的训练优化算法是一个由两项内容组成的函数：一个是损失项，用于衡量模型与数据的拟合度，另一个是正则化项，用于衡量模型复杂度。

 

举一个已经分享过的内容为例，多元线性回归模型：

 

多元线性回归的损失函数是离差平方和的形式，即最小二乘估计，公式如下：

 

 

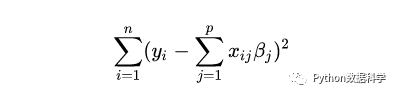
如果我们想通过正则化降低模型复杂度，可以在损失函数的基础上线性添加一个正则化项，这样就得到了一个新的结构风险函数，如下：

 

 

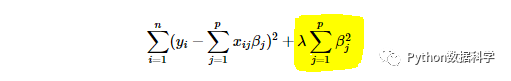
这里我们就添加了一个L2正则化项。先不讨论这个正则化项的类型，我们可以直观看到：在所有参数平方和前乘以了一个参数λ，把它叫正则化系数或者惩罚系数。这个惩罚系数是调节模型好坏的关键参数，我们通过两个极端的情况说明它是如何调节模型复杂度的。

 

• λ值为0：损失函数将与原来损失函数一样（即最小二乘估计形式），说明对参数权重β没有任何惩罚。
• λ为无穷大：在惩罚系数λ无穷大的情况下，为保证整个结构风险函数最小化，只能通过最小化所有权重系数β达到目的了，即通过λ的惩罚降低了参数的权重值，而在降低参数权重值的同时我们就实现了降低模型复杂度的效果。

 

当然，具体的惩罚程度还需要调节λ值来达到一个平衡的点，过度的惩罚会让模型出现欠拟合的情况。了解正则化项后，下面我来接着看一下这个惩罚项都可以是哪些类型。

 

▍正则化有哪些类型？

 

常用的正则化有两种L1和L2。如果了解KNN算法和聚类算法的都知道有两个常用的距离概念，曼哈顿距离和欧式距离，它们与正则化的对应关系是这样的：

 

• L1：曼哈顿距离（参数绝对求和）
• L2：欧氏距离（参数平方值求和）

 

在回归模型中，我们一般把的带有L1正则化项的回归模型叫做LASSO回归，而把带有L2正则化项的回归叫做岭回归。这里我们直接给出两种多元线性回归正则化的公式：

 

 

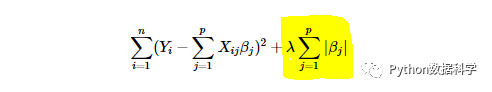
多元线性回归 L1正则化：Lasso回归

 

 

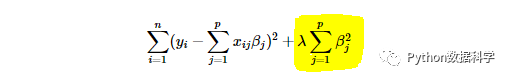
多元线性回归 L2正则化：Ridge回归

 

下面我们分别介绍一下LASSO回归和岭回归，然后对比L1和L2正则化的区别。

 

▍L2正则化：岭回归

 

岭回归的提出

 

我们在之前通过最小二乘法推导出多元线性回归的求解公式：

 

 

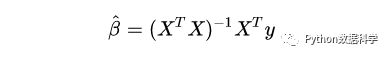
这个公式有一个问题：X不能为奇异矩阵，否则无法求解矩阵的逆。岭回归的提出恰好可以很好的解决这个问题，它的思路是：在原先的β的最小二乘估计中加一个小扰动λI，这样就可以保证矩阵的逆可以求解，使得问题稳定。公式如下：

 

 

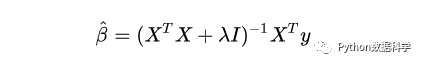
这个公式我们可以通过对上一节的结构化风险函数求偏导推出来，具体推导不进行展示了。

 

岭回归的几何意义

 

既然我们想最小化结构风险函数，那么我们可以通过限制其中的正则项来达到目的，因此可以将原来的结构风险函数变成另一种问题形式。

 

 

上式是对 β的平方和做数值上界限定，即所有β的平方和不超过参数 t。这时候，我们相当于拆分了原来的结构化分险函数，目标就转换为：最小化原来的训练样本误差，但是要遵循 β平方和小于 t 的条件。

 

以两个变量为例，通过图形来解释岭回归的几何意义，最小二乘解就相当于一个漏斗型，通过求解找到最小值。

 

 

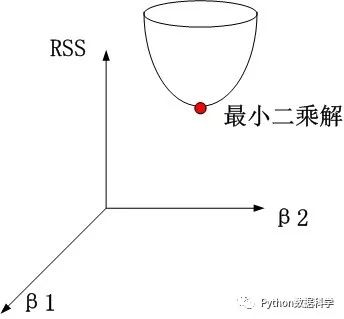
最小二乘求解：经验风险最小化

 

在原来的最小二乘求解基础上，加入下面的正则化的约束（几何图形中相当于一个圆柱体）。

 

 

 

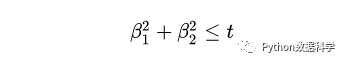
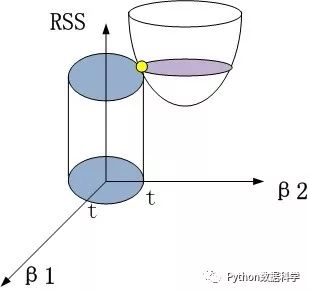
岭回归：结构风险最小化

 

公式中的 t 和 λ 是成反比的，也就是说t越小，惩罚程度越大，与sklearn中的正则化参数定义是一样的。

 

因此，如果我们减小t，圆柱体就会向内缩，导致与漏斗的交点向上移动，而向上移动的同时 β1 和β2的值也在减小，即达到了降低参数权重的效果。但是随着向上移动，结构化风险函数的值也越来越大了，趋于欠拟合的方向，这也就揭示了为什么说要选择一个合适的惩罚系数了。

 

▍L1正则化：LASSO回归

 

LASSO回归形式上与岭回归非常相似，只是将平方换成了绝对值。

 

 

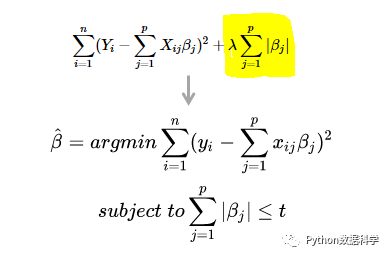
LASSO回归正则项的几何形式不再是一个圆柱体，而变为一个长方体了，这也是导致两种回归关于是否稀疏的根本原因。

 

▍L1和L2正则化有什么相同和不同？

 

1. 有偏估计

 

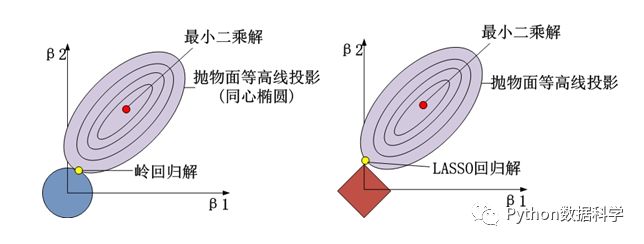
我们将前面的三维立体图形映射成二维（从上往下看），可以清晰地看到：求解的交点不再是最小二乘的最小值（红点），而变成了与正则项的交点（黄点）。这说明了LASSO回归和岭回归都是一种有偏估计，而最小二乘是一种无偏估计。

 

 

2. 能否使参数矩阵稀疏

 

前面我们说正则化是通过调整模型参数（数量和大小）来降低模型复杂度的，其实，这里说的数量和大小是和L1和L2正则化分别有着对应关系的。

 

• L1正则化：通过稀疏化（减少参数数量）来降低模型复杂度的，即可以将参数值减小到0。
• L2正则化：通过减少参数值大小来降低模型复杂的，即只能将参数值不断减小但永远不会减小到0。

 

这个区别可以从二维图中更好地观察出来：岭回归中两个图形（没有棱角）的交点永远不会落在两个轴上，而LASSO回归中，正则化的几何图形是有棱角的，可以很好的让交点落在某一个轴上。

 

 

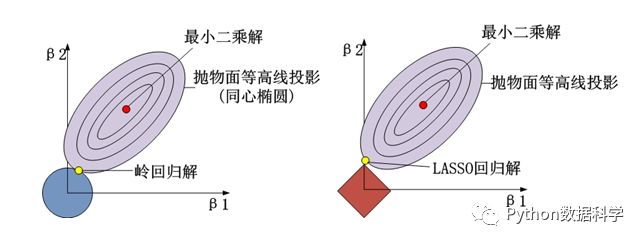
这种稀疏化的不同也导致了LASSO回归可以用于特征选择（让特征权重变为0从而筛选掉特征），而岭回归却不行。但是两种回归的效果还需要根据实际情况来选择，以及如何选择惩罚系数。关于稀疏化很有多内容，这里不进行展开。

 

3. 下降速度不同

 

两种回归的不同也可以反映在下降速度上，蓝色为岭回归的最小化下降曲线，红色为LASSO回归的下降曲线。

 

 

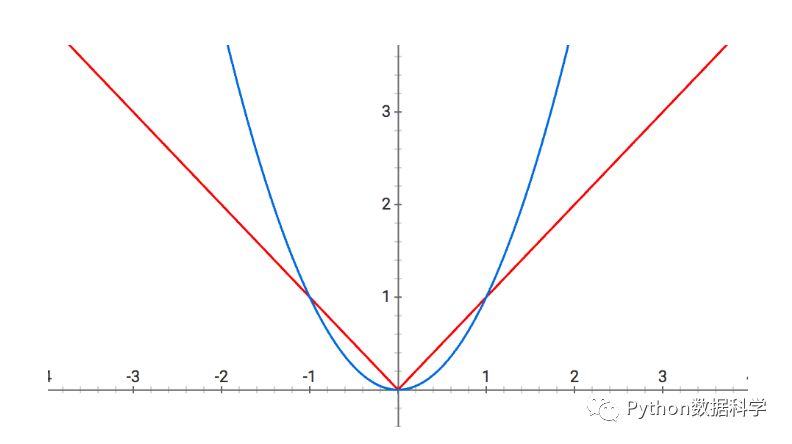
可以发现：最开始的时候岭回归下降的非常快，但是随着值越来越小，岭回归下降速度也越来越慢，当快接近0的时候，速度会非常慢，即很难减小到0。相反，LASSO回归是以恒定的速度下降的，相比于岭回归更稳定，下降值越接近近0时，下降速度越快，最后可以减小到0。

 

下面是一组岭回归和LASSO回归的特征系数随着模型不断迭代而变化的动态展示。

 

 

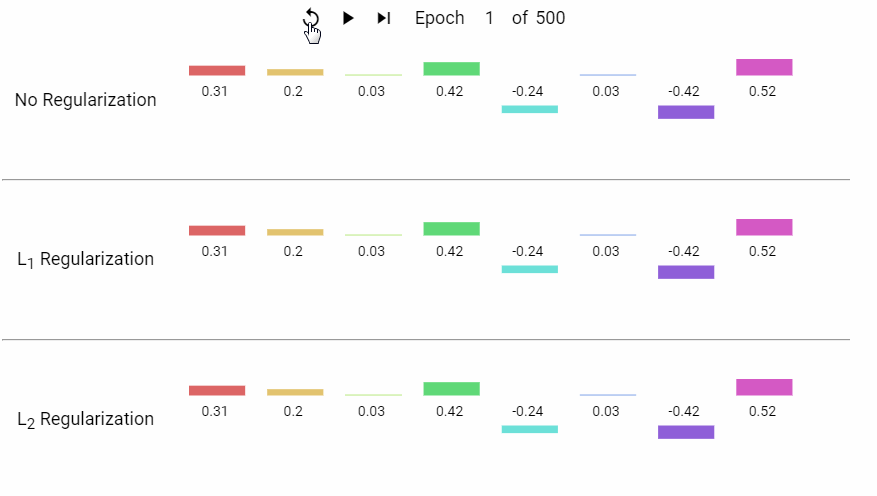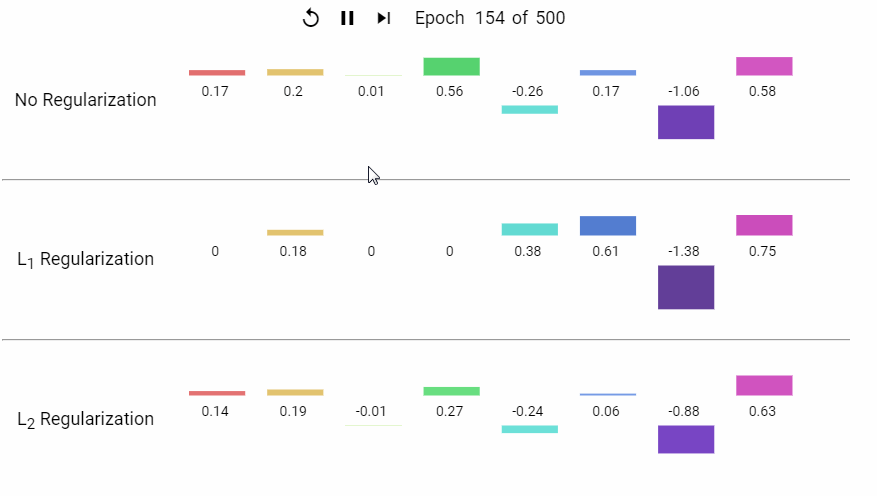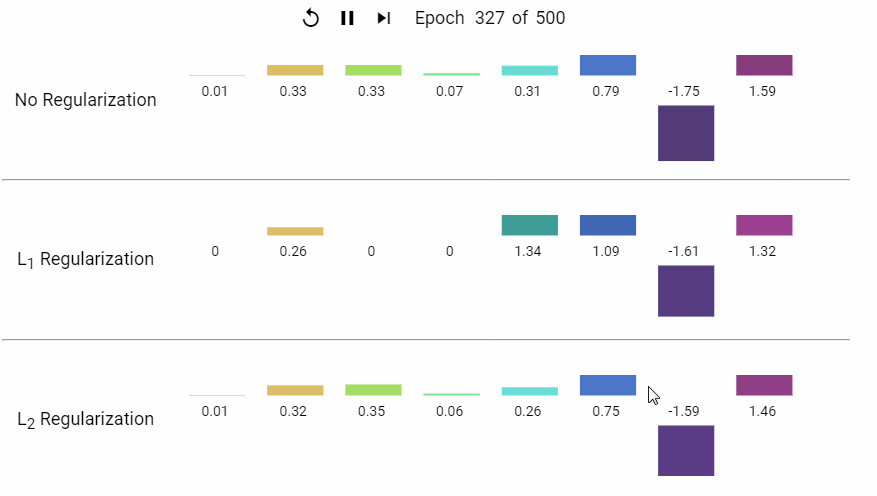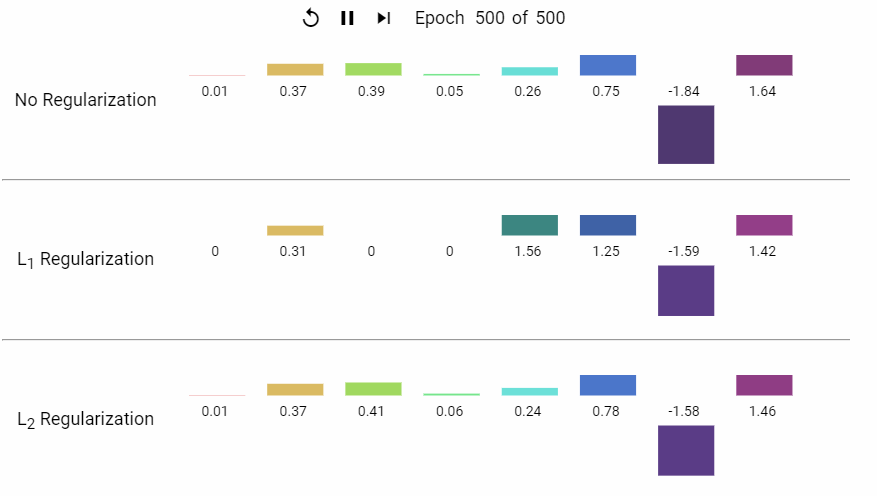
▍其它正则化类型？

 

L1和L2只是比较常用的范数，如果推广到一般的话，可以有非常多种的正则化。

 

 

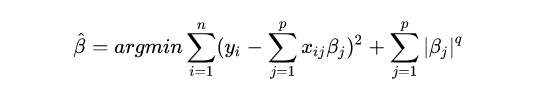
q可是是很多值

 

 

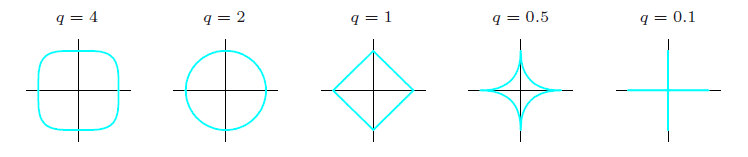
但是由于一些凸优化问题，L1和L2表现出来的效果是最好的，因此也被最常用到。

 

此外，还有一种介于L1和L2之间的一种正则化叫Elasticnet，像一种弹性网一样，现在被认为是处理多重共线性和变量筛选较好的收缩方法，而且损失的精度不会太多。

 

▍总结

 

本篇由浅入深地介绍了过拟合，正则化，以及LASSO回归和岭回归，希望通过本篇可以让你对正则化有一个清晰的认识，后续会介绍正则化相关编程方面的实战内容，以及如何选择参数，调节参数。

 

参考：

 

[1].http://f.dataguru.cn/thread-598486-1-1.html

 

[2].https://developers.google.com/machine-learning/

 

[3].https://towardsdatascience.com/

[4].https://blog.csdn.net/lyf52010/article/details/79822144