各种各样的激活函数(详细)
各种各样的激活函数(详细)
深入理解激活函数
各种各样的激活函数(表格对比)
https://blog.csdn.net/caip12999203000/article/details/127067360
二、常用激活函数解析
1、Sigmoid函数
1.1 公式

1.2 对应的图像

1.3 优点与不足之处
Sigmoid优点:
1、其值域为[0,1],非常适合作为模型的输出函数用于输出一个(0,1)范围内的概率值,可用于将预测概率作为输出的模型,比如用于表示二分类的类别或者用于表示置信度。
2、Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在0到1,因此它对每个神经元的输出进行了归一化。
3、该函数是连续可导的(即可微),可以提供非常平滑的梯度值,防止模型训练过程中出现突变的梯度(即避免「跳跃」的输出值)。
Sigmoid不足:
1、从其导数的函数图像上可以看到,其导数的最大值只有0.25,而且当x在[-5,5]的范围外时其导数值就已经几乎接近于0了。这种情况会导致训练过程中神经元处于一种饱和状态,反向传播时其权重几乎得不到更新,从而使得模型变得难以训练,这种现象被称为梯度消失问题。
2、其输出不是以0为中心而是都大于0的(这会降低权重更新的效率),这样下一层的神经元会得到上一层输出的全正信号作为输入,所以Sigmoid激活函数不适合放在神经网络的前面层而一般是放在最后的输出层中使用。
3、需要进行指数运算(计算机运行得较慢),计算量大及计算复杂度高,训练耗时;指数的越大其倒数就越小,容易产生梯度消失。
1.4 对应pytorch的代码
import torch
import torch.nn as nn
# Sigmoid函数
print('*'*25+"Sigmoid函数"+"*"*25)
m = nn.Sigmoid()
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

2、Tanh函数
2.1 公式

2.2 对应的图像

2.3 优点与不足之处
Tanh优点:
1、在分类任务中,双曲正切函数(Tanh)逐渐取代 Sigmoid 函数作为标准的激活函数,其具有很多神经网络所钟爱的特征。它是完全可微分的,反对称,对称中心在原点。
2、输出是S型曲线,具备打破网络层与网络层之间的线性关系,可以把网络层输出非线形地映射到 (−1,1) 区间里。负输入将被强映射为负,而零输入被映射为接近零;tanh 的输出间隔为1且值域是以0为中心的[-1,1](可以解决Sigmoid激活函数输出不以0为中心的问题。)
3、在一般的二元分类问题中,tanh 函数用于隐藏层,而 sigmoid 函数用于输出层,但这并不是固定的,需要根据特定问题进行调整。
Tanh不足:
1、当输入较大或较小时,输出几乎是平滑的并且梯度较小,这不利于权重更新。
2、Tanh函数也需要进行指数运算,所以其也会存在计算复杂度高且计算量大的问题。
3、当神经网络的层数增多的时候,由于在进行反向传播的时候,链式求导,多项相乘,函数进入饱和区(导数接近于零的地方)就会逐层传递,这种现象被称为梯度消失。
2.4 对应pytorch的代码
import torch
import torch.nn as nn
# Tanh函数
print('*'*25+"Tanh函数"+"*"*25)
m = nn.Tanh()
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

3、ReLU
ReLu, 全称是 Rectified Linear Unit, 中文名称是线性整流函数
3.1 公式

3.2 对应的图像

3.3 优点与不足之处
ReLU函数:
1、ReLU 函数在正输入时是线性的,收敛速度快,计算速度快,同时符合恒等性的特点。当输入为正时,由于导数是1,能够完整传递梯度,不存在梯度消失的问题(梯度饱和问题)。
2、计算速度快。ReLU 函数中只存在线性关系且无论是函数还是其导数都不包含复杂的数学运算,因此它的计算速度比 sigmoid 和 tanh 更快。
3、当输入大于0时,梯度为1,能够有效避免链式求导法则梯度相乘引起的梯度消失和梯度爆炸;计算成本低。
4、它保留了 step 函数的生物学启发(只有输入超出阈值时神经元才激活),不过当输入为正的时候,导数不为零,从而允许基于梯度的学习(尽管在 x=0 的时候,导数是未定义的)。当输入为负值的时候,ReLU 的学习速度可能会变得很慢,甚至使神经元直接无效,因为此时输入小于零而梯度为零,从而其权重无法得到更新,在剩下的训练过程中会一直保持静默。
ReLU不足:
1、ReLU的输入值为负的时候,输出始终为0,其一阶导数也始终为0,这样会导致神经元不能更新参数,也就是神经元不学习了,这种现象叫做“Dead Neuron”。为了解决ReLU函数这个缺点,在ReLU函数的负半区间引入一个泄露(Leaky)值,所以称为Leaky ReLU函数。
2、与Sigmoid一样,其输出不是以0为中心的(ReLU的输出为0或正数)。
3、ReLU在小于0的时候梯度为零,导致了某些神经元永远被抑制,最终造成特征的学习不充分;这是典型的 Dead ReLU 问题,所以需要改进随机初始化,避免将过多的负数特征送入ReLU。
3.4 对应pytorch的代码
import torch
import torch.nn as nn
# Relu函数
print('*'*25+"Relu函数"+"*"*25)
m = nn.ReLU()
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

4、Leaky ReLU函数
Leaky 渗漏的; 有漏洞的; 有漏隙的
4.1 公式

4.2 对应的图像

4.3 改进以及不足之处
Leaky ReLU函数(ReLU的改进):
1、与ReLU函数相比,把x的非常小的线性分量给予负输入(0.01x)来调整负值的零梯度问题;有助于扩大 ReLU 函数的范围,通常𝜆λ的值为 0.01 左右;函数范围是负无穷到正无穷。
2、LeakyRelu激活函数通过在负半轴添加一个小的正斜率(使得负轴的信息不会全部丢失)来解决ReLU激活函数的“死区”问题,该斜率参数𝜆λ是手动设置的超参数,一般设置为0.01。通过这种方式,LeakyRelu激活函数可以确保模型训练过程中神经元的权重在输入小于0的情况下依然会得到更新。
3、不会出现 Dead ReLu 问题,但是关于输入函数f(x) 的部分容易出现梯度爆炸的情况是一样的,所以必要时,也可以搭配 sigmoid 或 tanh 使用。
Leaky ReLU不足:
1、经典(以及广泛使用的)ReLU 激活函数的变体,带泄露修正线性单元(Leaky ReLU)的输出对负值输入有很小的坡度。由于导数总是不为零,这能减少静默神经元的出现,允许基于梯度的学习(虽然会很慢)。
2、从理论上讲,Leaky ReLU 具有 ReLU 的所有优点,而且 Dead ReLU 不会有任何问题,但在实际操作中,尚未完全证明 Leaky ReLU 总是比 ReLU 更好。
4.4 对应pytorch的代码
import torch
import torch.nn as nn
# Leaky Relu函数
print('*'*25+"Leaky Relu函数"+"*"*25)
m = nn.LeakyReLU(negative_slope=0.1) #negative_slope是个常数
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

5、PReLU函数
Parametric Rectified Linear Unit
’对应的论文链接:https://arxiv.org/abs/1502.01852v1
5.1 公式

5.2 对应的图像

5.3 改进以及不足之处
PReLU函数(ReLU的改进):
1、在负值域,PReLU的斜率较小,这也可以避免Dead ReLU问题。与ELU相比,PReLU在负值域是线性运算。尽管斜率很小,但不会趋于0。
2、公式与Leaky ReLu相似,但并不完全一样。𝛼可以是常数,或自适应调整的参数。也就是说,如果让a自适应,那么PReLu会在反向传播时更新参数a。
3、参数α通常为0到1之间的数字,并且通常相对较小。
(1)如果𝛼 = 0,则f(x)变为ReLU。
(2)如果𝛼 > 0,则f(x)变为leaky ReLU。
(3)如果𝛼是可学习的参数,则f(x)变为PReLU。
PReLU不足:
这留给你们探索了!
5.4 对应pytorch的代码
import torch
import torch.nn as nn
# PRelu函数
print('*'*25+"PRelu函数"+"*"*25)
m = nn.PReLU(num_parameters=1) #num_parameters是个可训练参数
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

6、RReLU函数
RReLU 随机带泄露的修正线性单元(Randomized Leaky Rectified Linear Unit,RReLU)
对应论文的链接:https://arxiv.org/pdf/1505.00853.pdf
6.1 公式

6.2 对应的图像

6.3 改进以及不足之处
RReLU函数(ReLU的改进):
1、RReLU和PReLU的表达式一样,但𝛼α参数不一样,这里的𝛂α是个随机震荡的数,范围(pytorch):1/8~1/3。(对应图的参数为lower =1/8,upper =1/3)
3、RReLU(随机校正线性单元)。在RReLU中,负部分的斜率在训练中被随机化到给定的范围内,然后再测试中被固定。在最近的Kaggle国家数据科学碗(NDSB)比赛中,由于RReLU的随机性,它可以降低过拟合。因此RReLU是有利的,而在大数据的情况下,未来还需要做更多的研究。
RReLU不足:
这留给你们探索!
6.4 对应pytorch的代码
import torch
import torch.nn as nn
# RRelu函数
print('*'*25+"RRelu函数"+"*"*25)
m = nn.RReLU(lower=0.1, upper=0.3) # 这里的参数属于(lower,upper)之间的震荡随机数
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

7、ELU函数
ELU (Exponential Linear Units)
对应论文的链接:https://arxiv.org/abs/1511.07289
7.1 公式

7.2 对应的图像

7.3 改进以及不足之处
ELU函数(ReLU的改进):(上图的α值为1.0)
1、ELU在负值时是一个指数函数(使激活的平均值接近零),具有软饱和特性,对噪声更鲁棒,抗干扰能力强;在较小的输入下会饱和至负值,从而减少前向传播的变异和信息。
2、均值向零加速学习。通过减少偏置偏移的影响,使正常梯度接近于单位自然梯度,可以使学习更快。
3、输出有负值,使得其输出的平均值为0;右侧的正值特性,可以像relu一样缓解梯度消失的问题。
ELU不足:
1、ELu 也是为了解决 Dead ReLu 而提出的改进型。计算上稍微比 Leaky ReLu 复杂一点,但从精度看似乎并未提高多少。
2、尽管理论上比 ReLU 要好,但目前在实践中没有充分的证据表明 ELU 总是比 ReLU 好。
7.4 对应pytorch的代码
import torch
import torch.nn as nn
# ELU函数
print('*'*25+"ELU函数"+"*"*25)
m = nn.ELU(alpha=1.0) # 这里的参数alpha默认为1
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

8、SELU函数
Selu函数又称为Self-Normalizing Neural Network(SNN)
对应论文的链接:https://arxiv.org/abs/1706.02515
8.1 公式

8.2 对应的图像

8.3 改进以及不足之处
SELU函数(ReLU的改进):(上图的𝛼=1.67 and 𝝀=1.05.)
1、当其中参数α=1.67 , λ=1.05时,在网络权重服从正态分布的条件下,各层输出的分布会向标准正态分布靠拢。这种[自我标准化]的特性可以避免梯度消失和爆炸。
2、SELU激活函数是在自归一化网络中定义的,通过调整均值和方差来实现内部的归一化,这种内部归一化比外部归一化更快,这使得网络收敛得更快。
3、SELU是给ELU乘上一个系数,该系数大于1。在这篇paper Self-Normalizing Neural Networks中,作者提到,SELU可以使得输入在经过一定层数之后变为固定的分布。以前的ReLU、P-ReLU、ELU等激活函数都是在负半轴坡度平缓,这样在激活的方差过大时可以让梯度减小,防止了梯度爆炸,但是在正半轴其梯度简答的设置为了1。而SELU的正半轴大于1,在方差过小的时候可以让它增大,但是同时防止了梯度消失。这样激活函数就有了一个不动点,网络深了之后每一层的输出都是均值为0,方差为1。
SELU不足:
留给你们探索!
8.4 对应pytorch的代码
import torch
import torch.nn as nn
# SELU函数
print('*'*25+"SELU函数"+"*"*25)
m = nn.SELU() # 这里的参数默认alpha=1.67,scale=1.05
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

9、CELU函数
Continuously Differentiable Exponential Linear Units。
对应论文的链接:https://arxiv.org/abs/1704.07483
9.1 公式

9.2 对应的图像

9.3 官方给的配置
由于没找到什么相关的资料,所以这里就给pytorch官方实现的参数。
CELU函数(ReLU的改进):(右图的𝛼=1.0.)
1、官方配置:
alpha – the α value for the CELU formulation. Default: 1.0
inplace – can optionally do the operation in-place. Default: False
CELU不足:
暂无
9.4 对应pytorch的代码
import torch
import torch.nn as nn
# CELU函数
print('*'*25+"CELU函数"+"*"*25)
m = nn.CELU(alpha=1.0) # 这里的参数默认alpha=1.0
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

10 、GELU函数
GELU是一种常见的激活函数,全称为“Gaussian Error Linear Unit”
对应论文的链接:https://arxiv.org/abs/1606.08415
10.1 公式

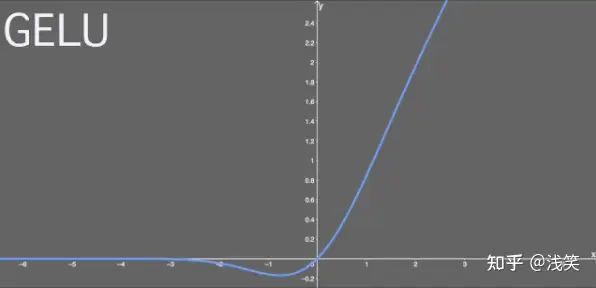
10.2 对应的图像

10.3 优点以及不足之处
GELU优点:
1、当方差为无穷大,均值为0的时候,GeLU就等价于ReLU了。GELU可以当作为RELU的一种平滑策略。GELU是非线性输出,具有一定的连续性。GELU有一个概率解释,因为它是一个随机正则化器的期望。
2、研究学者尝试使用一个依赖于输入本身的概率统计量为激活函数提供随机正则性,同时保持输入信息,得到了一个更好的激活函数,即高斯误差线性单元,形式如下:
GELU(x) = x ∗ P(X≤x) = x ∗ ϕ(x)
由于上面这个函数是无法直接计算的,研究者在研究过程中发现GELU函数可以被近似地表示为
GELU(x)=0.5∗x∗(1+tanh(√(2/π )∗(x+0.044715x^3) )
3、GELU的实用技巧。首先,建议在使用GELU训练时使用具有动量的优化器,这是深度神经网络的标准。其次,使用对高斯分布的累积分布函数的密切近似是很重要的。
GELU不足:
留给大家探索!
10.4 对应pytorch的代码
import torch
import torch.nn as nn
# GELU函数
print('*'*25+"GELU函数"+"*"*25)
m = nn.GELU()
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

11、ReLU6函数
ReLU6 就是普 通的 ReLU 但是限制最大输出为 6
ReLU6函数是一种修正线性单元(Rectified Linear Unit)
对应论文的链接:https://arxiv.org/abs/1704.04861v1
11.1 对应的公式

11.2 对应的图像

11.3 改进以及不足之处
ReLU6函数(ReLU的改进):(右图的𝛼α=1.0.)
1、为了在移动设备float16/int8的低精度的时候也能有很好的数值分辨率。如果对ReLU的激活范围不加限制,输入范围为0到正无穷,如果激活值非常大,分布在一个很大的范围内,则低精度的float16/int8无法很好地精确描述如此大范围的数值,带来精度损失。
ReLU6不足:
留给大家探索!
11.4 对应pytorch的代码
import torch
import torch.nn as nn
# ReLU6函数
print('*'*25+"ReLU6函数"+"*"*25)
m = nn.ReLU6()
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

12、Swish函数
谷歌大脑团队提出了新型激活函数 Swish,团队实验表明使用 Swish 直接替换 ReLU 激活函数总体上可令 DNN 的测试准确度提升。此外,该激活函数的形式十分简单,且提供了平滑、非单调等特性从而提升了整个神经网络的性能。
对应论文链接:https://arxiv.org/pdf/1710.05941v2.pdf
12.1 公式

12.2 对应的图像

12.3 优点以及不足之处
Swish优点:(右图的𝛽β=1.0.)
1、和Relu一样,没有上边界,因此不会出现梯度饱和的现象(避免过拟合)。
2、有下边界,可以产生更强的正则化效果(x左半轴慢慢趋近于0)
3、x<0非单调函数
4、平滑(处处可导,更容易训练)
Swish不足:
留给你们探索!
12.4 对应pytorch的代码
import torch
import torch.nn as nn
from torch.nn.modules.module import Module
from torch.nn import functional as F
from torch import Tensor
# Swish函数
# 由于旧版pytorch没找到Swich,自己整了一个
class Swish(Module):
__constants__ = ['beta']
beta: int
def __init__(self, beta: int = 1) -> None:
super(Swish, self).__init__()
self.beta = beta
def forward(self, input: Tensor) -> Tensor:
return input*torch.sigmoid(input*self.beta)
print('*'*25+"Swish函数"+"*"*25)
m = Swish()
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:

13、Hardswish函数
对应论文的链接:https://arxiv.org/abs/1905.02244
13.1 公式

13.2 对应的图像

13.3 优点以及不足之处
Hardswich优点:
1、激活函数h-swish是MobileNet V3相较于V2的一个创新,是在谷歌大脑2017年的论文Searching for Activation Functions中swish函数的基础上改进而来,用于替换V2中的部分ReLU6。
2、作者选择了ReLU6作为这个近似函数,有两个原因:在几乎所有的软件和硬件框架上都可以使用ReLU6的优化实现;ReLU6能在特定模式下消除由于近似sigmoid的不同实现而带来的潜在的数值精度损失。
3、作者认为,随着网络的深入,应用非线性激活函数的成本会降低,能够更好的减少参数。
Hardswich不足:
留给你们探索!
13.4 对应pytorch的代码
import torch
import torch.nn as nn
# Hardswish函数
print('*'*25+"Hardswish函数"+"*"*25)
m = nn.Hardswish()
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:
14、SiLU函数
对应论文的链接:https://arxiv.org/pdf/1702.03118v3.pdf
14.1 公式

14.2 对应的图像

14.3 函数特点
SiLU函数:
1、Swish激活函数具备无上界有下界、平滑、非单调的特性,Swish在深层模型上效果优于ReLU。
表达式:
swish(x)=x⋅sigmoid(βx)
β是个常数或者可训练的参数,当β=1时,我们也称作SiLU激活函数。
14.4 对应pytorch的代码
import torch
import torch.nn as nn
# SiLU函数
print('*'*25+"SiLU函数"+"*"*25)
m = nn.SiLU()
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:
15、Softplus函数
15.1 公式

15.2 对应的图像

15.3 函数特点
Softplus函数:
Softplus函数可以看作是ReLU函数的平滑,加了1是为了保证非负性。
2、它是一种和 ReLu 函数功能作用极象的函数,并且在很多新的模型里,作为 ReLu 的替代。相对于ReLu 或 LeakyReLu 来说,Softplus 有个非常「致命」的优点,就是它在0点处是可导的。不过相对于 ReLu 的粗暴简单,这个函数的运算耗费时间相对较多。
15.4 对应pytorch的代码
import torch
import torch.nn as nn
# Softplus函数
print('*'*25+"Softplus函数"+"*"*25)
m = nn.Softplus(beta=1.0)# 这里的参数默认beta=1.0
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:
16、Mish函数
对应论文的链接:https://arxiv.org/pdf/1908.08681v3.pdf
16.1 公式

16.2 对应的图像

16.3 函数特点
Mish优点:
1、Mish激活函数无边界(即正值可以达到任何高度)避免了由于封顶而导致的饱和。理论上对负值的轻微允许允许更好的梯度流,而不是像ReLU中那样的硬零边界。
最后,可能也是最重要的,目前的想法是,平滑的激活函数允许更好的信息深入神经网络,从而得到更好的准确性和泛化。
2、Mish函数具有以下几个特点:
1、无上界有下界(没有上限),这样可以保证没有饱和区域,因此在训练过程中不会有梯度消失的问题,这个和relu后面的激活函数一样。有下限的话能够保证具有一定的regularization effect,这对于神经网络训练来说是一个很好的特性。
2、非单调性函数,输入较小负数的时候往往梯度回传也会很小,这样会导致收敛较慢,但是如果输入较大负数的时候不缩小的话,又容易梯度爆炸。这种性质有助于小的负值,从而稳定网络梯度流。
3、无穷阶连续性和光滑性,Mish函数是光滑函数,具有较好的泛化能力和结果的有效优化能力,可以提高结果的质量。
16.4 对应pytorch的代码
import torch
import torch.nn as nn
from torch.nn.modules.module import Module
from torch.nn import functional as F
from torch import Tensor
# Mish函数
class Mish(Module):# 由于我使用是pytorch老版本没有Mish函数,自己整了一个
__constants__ = ['beta', 'threshold']
beta: int
threshold: int
def __init__(self, beta: int = 1, threshold: int = 20) -> None:
super(Mish, self).__init__()
self.beta = beta
self.threshold = threshold
def forward(self, input: Tensor) -> Tensor:
return input*torch.tanh(F.softplus(input, self.beta, self.threshold))
def extra_repr(self) -> str:
return 'beta={}, threshold={}'.format(self.beta, self.threshold)
print('*'*25+"Mish函数"+"*"*25)
m = Mish()
# input = torch.randn(2)
input = torch.range(0,2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:
17、 Softmax函数
17.1 公式

17.2 对应的图像

这里使用梯度无法求导,所以导函数图像是一个y=0的直线。
17.3 优点以及不足之处
Softmax函数:
Softmax激活函数的特点:
1、在零点不可微,负输入的梯度为零,这意味着对于该区域的激活,权重不会在反向传播期间更新,因此会产生永不激活的死亡神经元。
2、将预测结果转化为非负数、预测结果概率之和等于1。
3、经过使用指数形式的Softmax函数能够将差距大的数值距离拉的更大。在深度学习中通常使用反向传播求解梯度进而使用梯度下降进行参数更新的过程,而指数函数在求导的时候比较方便.
Softmax不足:
使用指数函数,当输出值非常大的话,计算得到的数值也会变的非常大,数值可能会溢出。
17.4 对应pytorch的代码
import torch
import torch.nn as nn
# Softmax函数
print('*'*25+"Softmax函数"+"*"*25)
m = nn.Softmax(dim=0) # 维度为0
input = torch.randn(2)
print("原:",input)
print("结果:",m(input))
print('*'*50)
对应的结果:
三、 绘图代码(部分图像)
# https://blog.csdn.net/huadushao/article/details/107094804?ops_request_misc=&request_id=&biz_id=102&utm_term=pytorch%20%E6%B1%82%E5%AF%BC%E5%87%BD%E6%95%B0%E5%9B%BE%E5%83%8F&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-0-107094804.142^v50^control,201^v3^add_ask&spm=1018.2226.3001.4187
import torch
import numpy as np
import matplotlib.pylab as plt
import sys
from matplotlib import pyplot as plt
from IPython import display
from matplotlib import style
from torch.nn.modules.module import Module
from torch.nn import functional as F
from torch import Tensor
def xyplot(x_vals, y_vals, name):
plt.rcParams['figure.figsize'] = (5, 3.5)
plt.grid(c='black',linewidth=0.08)
plt.plot(x_vals.detach().numpy(), y_vals.detach().numpy(), label = name, linewidth=1.5)
font = {'family': 'SimHei'}; # 中文字体
plt.legend(loc='upper left',prop=font)
#dark_background, seaborn, ggplot
# plt.style.use("seaborn")
ax = plt.gca()
ax.spines['right'].set_color("none")
ax.spines['top'].set_color("none")
ax.spines['bottom'].set_position(("data",0))
ax.spines['left'].set_position(("data",0))
ax.spines['bottom'].set_linewidth(0.5)
ax.spines['left'].set_linewidth(0.5)
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
# 激活函数以及导函数
def func_(y_func,func_n,save_=None,x_low=-6.0,x_top=6.0):
x = torch.arange(-6.0, 6.0, 0.1, requires_grad=True)
y = y_func(x)
xyplot(x, y, '原函数')
#导数
y.sum().backward()
xyplot(x, x.grad, "导函数")
plt.title(f"{func_n}(x)")
if save_ is not None:
plt.draw()
plt.savefig(f"./{func_n}.jpg")
plt.close()
plt.show()
# 由于我使用的pytorch版本没有Mish函数,所以整了一个
class Mish(Module):
__constants__ = ['beta', 'threshold']
beta: int
threshold: int
def __init__(self, beta: int = 1, threshold: int = 20) -> None:
super(Mish, self).__init__()
self.beta = beta
self.threshold = threshold
def forward(self, input: Tensor) -> Tensor:
return input*torch.tanh(F.softplus(input, self.beta, self.threshold))
def extra_repr(self) -> str:
return 'beta={}, threshold={}'.format(self.beta, self.threshold)
# 没找到Swich,so再整了一个
class Swish(Module):
__constants__ = ['beta']
beta: int
def __init__(self, beta: int = 1) -> None:
super(Swish, self).__init__()
self.beta = beta
def forward(self, input: Tensor) -> Tensor:
return input*torch.sigmoid(input*self.beta)
# RReLU
func_(torch.nn.RReLU(),"RReLU",True)
# ELU
func_(torch.nn.ELU(),"ELU",True)
# SELU
func_(torch.nn.SELU(),"SELU",True)
# CELU
func_(torch.nn.CELU(),"CELU",True)
# GELU
func_(torch.nn.GELU(),"GELU",True)
# ReLU6
func_(torch.nn.ReLU6(),"ReLU6",True)
# Swish
func_(Swish(),"Swish",True)
# Hardswish
func_(torch.nn.Hardswish(),"Hardswish",True)
# SiLU
func_(torch.nn.SiLU(),"SiLU",True)
# Softplus
func_(torch.nn.Softplus(),"Softplus",True)
# Mish
func_(Mish(),"Mish",True)
# Softmax
func_(torch.nn.Softmax(),"Softmax",True)
————————————————
版权声明:本文为CSDN博主「小wu学cv」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/caip12999203000/article/details/127067360
4. 常用的激活函数:sigmoid,Tanh,ReLU,Leaky ReLU,PReLU,ELU,Maxout,selu
(1) sigmoid函数
sigmoid函数又称 Logistic函数,用于隐层神经元输出,取值范围为(0,1),可以用来做二分类。
sigmoid函数表达式:
sigmoid函数的几何形状是一条S型曲线,图像如下:
Sigmoid激活函数

优点:
Sigmoid函数的输出在(0,1)之间,输出范围有限,优化稳定,可以用作输出层。
连续函数,便于求导。
缺点:
sigmoid函数在变量取绝对值非常大的正值或负值时会出现饱和现象,意味着函数会变得很平,并且对输入的微小改变会变得不敏感。在反向传播时,当梯度接近于0,权重基本不会更新,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。
sigmoid函数的输出不是0均值的,会导致后层的神经元的输入是非0均值的信号,这会对梯度产生影响。
计算复杂度高,因为sigmoid函数是指数形式。
(2) Tanh函数
Tanh函数也称为双曲正切函数,取值范围为[-1,1]。
Tanh函数定义如下:

函数图像如下:
tanh激活函数

实际上,Tanh函数是 sigmoid 的变形:
Tanh函数是 0 均值的,因此实际应用中 Tanh 会比 sigmoid 更好。但是仍然存在梯度饱和与exp计算的问题。
(3) ReLU函数
整流线性单元(Rectified linear unit,ReLU)是现代神经网络中最常用的激活函数,大多数前馈神经网络默认使用的激活函数。
ReLU函数定义如下:

函数图像如下:
RELU函数

优点:
使用ReLU的SGD算法的收敛速度比 sigmoid 和 tanh 快。
在x>0区域上,不会出现梯度饱和、梯度消失的问题。
计算复杂度低,不需要进行指数运算,只要一个阈值就可以得到激活值。
缺点:
ReLU的输出不是0均值的。
Dead ReLU Problem(神经元坏死现象):ReLU在负数区域被kill的现象叫做dead
relu。ReLU在训练的时很“脆弱”。在x<0时,梯度为0。这个神经元及之后的神经元梯度永远为0,不再对任何数据有所响应,导致相应参数永远不会被更新。
产生这种现象的两个原因:参数初始化问题;learning rate太高导致在训练过程中参数更新太大。
解决方法:采用Xavier初始化方法,以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
(4) Leaky ReLU函数
渗漏整流线性单元(Leaky ReLU),为了解决dead ReLU现象。用一个类似0.01的小值来初始化神经元,从而使得ReLU在负数区域更偏向于激活而不是死掉。这里的斜率都是确定的。
leakyrelu激活函数是relu的衍变版本,主要就是为了解决relu输出为0的问题。如图所示,在输入小于0时,虽然输出值很小但是值不为0。
leakyrelu激活函数一个缺点就是它有些近似线性,导致在复杂分类中效果不好。
leaky relu函数

(5) PReLU
参数整流线性单元(Parametric Rectified linear unit,PReLU),用来解决ReLU带来的神经元坏死的问题。
公式:
f ( x ) = m a x ( α x , x ) f(x)=max(\alpha x,x) f(x)=max(αx,x)
其中不是固定的,是通过反向传播学习出来的。
(6) ELU
指数线性单元(ELU):具有relu的优势,没有Dead ReLU问题,输出均值接近0,实际上PReLU和Leaky ReLU都有这一优点。有负数饱和区域,从而对噪声有一些鲁棒性。可以看做是介于ReLU和Leaky ReLU之间的一个函数。当然,这个函数也需要计算exp,从而计算量上更大一些。
ELU函数

(7) Maxout
maxout是一个函数逼近器,对于一个标准的MLP网络来说,如果隐藏层的神经元足够多,那么理论上我们是可以逼近任意的函数的。类似的,对于maxout 网络也是一个函数逼近器。
Maxout隐藏层每个神经元的计算公式如下:
h i ( x ) = max j ∈ [ 1 , k ] z i j h_i(x)=\max_{j\in [1,k]} z_ij hi(x)=j∈[1,k]maxzij
上面的公式就是maxout隐藏层神经元i的计算公式。其中,k就是maxout层所需要的参数了,由我们人为设定大小。就像dropout一样,也有自己的参数p(每个神经元dropout概率),maxout的参数是k。公式中Z的计算公式为:
z i j = x T W . . i j + b i j z_ij=x^T W_..ij + b_ij zij=xTW..ij+bij
权重w是一个大小为(d,m,k)三维矩阵,b是一个大小为(m,k)的二维矩阵,这两个就是我们需要学习的参数。如果我们设定参数k=1,那么这个时候,网络就类似于以前我们所学普通的MLP网络。
Maxout是通过分段线性函数来拟合所有可能的凸函数来作为激活函数的,但是由于线性函数是可学习,所以实际上是可以学出来的激活函数。具体操作是对所有线性取最大,也就是把若干直线的交点作为分段的边界,然后每一段取最大。
优点:
Maxout的拟合能力非常强,可以拟合任意的凸函数。
Maxout具有ReLU的所有优点,线性、不饱和性。
不会出现神经元坏死的现象。
缺点:
增加了参数量。
关于maxout的讲解可以参看这篇文章Maxout网络学习。
(8) SELU
扩展型指数线性单元激活函数比较新,介绍它的论文包含长达 90 页的附录(包括定理和证明等)。当实际应用这个激活函数时,必须使用 lecun_normal 进行权重初始化。如果希望应用 dropout,则应当使用 AlphaDropout。
论文作者已经计算出了公式的两个值:α 和 λ,SELU示例图:
SELU函数

可以看到,它们的小数点后还有很多位,这是为了绝对精度。而且它们是预先确定的,也就是说我们不必担心如何为这个激活函数选取合适的 α 值。
说实话,这个公式看起来和其它公式或多或少有些类似。所有新的激活函数看起来就像是其它已有的激活函数的组合。
也就是说,如果输入值
x 大于 0,则输出值为 x 乘以 λ;如果输入值 x 小于 0,则会得到一个奇异函数——它随 x 增大而增大并趋近于 x 为 0 时的值
0.0848。本质上看,当 x 小于 0 时,先用 α 乘以 x 值的指数,再减去 α,然后乘以 λ 值。
SELU 激活能够对神经网络进行自归一化(self-normalizing)。这是什么意思?
首先,我们先看看什么是归一化(normalization)。简单来说,归一化首先是减去均值,然后除以标准差。因此,经过归一化之后,网络的组件(权重、偏置和激活)的均值为 0,标准差为 1。而这正是 SELU 激活函数的输出值。
均值为
0 且标准差为 1 又如何呢?在初始化函数为 lecun_normal 的假设下,网络参数会被初始化一个正态分布(或高斯分布),然后在
SELU
的情况下,网络会在论文中描述的范围内完全地归一化。本质上看,当乘或加这样的网络分量时,网络仍被视为符合高斯分布。我们就称之为归一化。反过来,这又意味着整个网络及其最后一层的输出也是归一化的。
下面引述一段论文的解释,说明了他们得到这个激活函数的方式,我认为这很重要:
SELU 允许构建一个映射 g,其性质能够实现 SNN(自归一化神经网络)。SNN 不能通过(扩展型)修正线性单元(ReLU)、sigmoid
单元、tanh 单元和 Leaky ReLU
实现。这个激活函数需要有:(1)负值和正值,以便控制均值;(2)饱和区域(导数趋近于零),以便抑制更低层中较大的方差;(3)大于 1
的斜率,以便在更低层中的方差过小时增大方差;(4)连续曲线。后者能确保一个固定点,其中方差抑制可通过方差增大来获得均衡。我们能通过乘上指数线性单元(ELU)来满足激活函数的这些性质,而且
λ>1 能够确保正值净输入的斜率大于 1。
优点:
内部归一化的速度比外部归一化快,这意味着网络能更快收敛;
不可能出现梯度消失或爆炸问题,见 SELU 论文附录的定理 2 和 3。
缺点:
这个激活函数相对较新——需要更多论文比较性地探索其在 CNN 和 RNN 等架构中应用。
原文链接:https://blog.csdn.net/u013705056/article/details/111373841
==========================================
42个激活函数的全面总结
2015 年 11 月,wikipedia的用户 Laughinthestocks 首次引入了“激活函数表”。从那时开始到现在,维基百科页面已经发生了 391 次更改。在本文中,我通过自己写的一个程序来挖掘截至 2022 年 4 月 22 日时维基百科页面历史中的每个唯一激活函数。本文还提供了针对激活函数的适当研究论文的附加链接,如果没有或者在无法找到特定研究论文的情况下,提供了相关的相关论文。
例如:通常人们会将 tanh 用于 FNN,将 ReLU 用于 CNN。
如果我们包括 Identity Activation 函数,这个列表将包含 42 个激活函数,这里面肯定有没有见过的。
Binary step

公式
导数

Logistic, sigmoid, or soft step
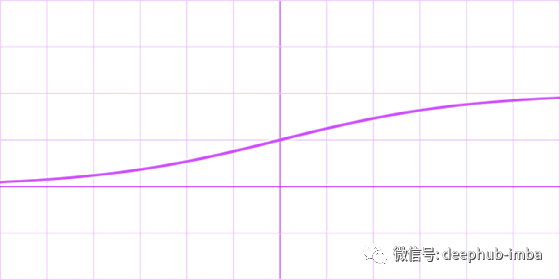
公式:

导数

还有双极 sigmoid(1.f-expf(-x)) / (1.f + expf(-x))
ElliotSig 或 Softsign
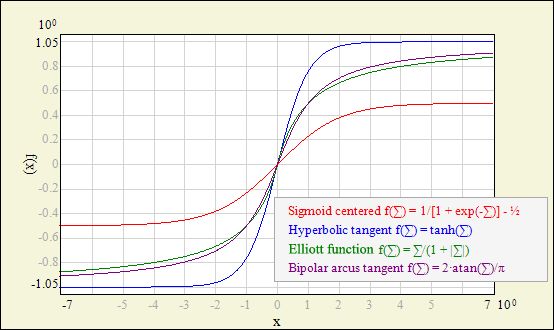
公式:
导数
双曲正切 (tanh)
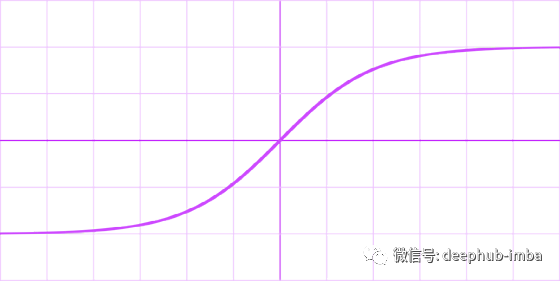
公式

导数
Arctangent / Arctan / atan
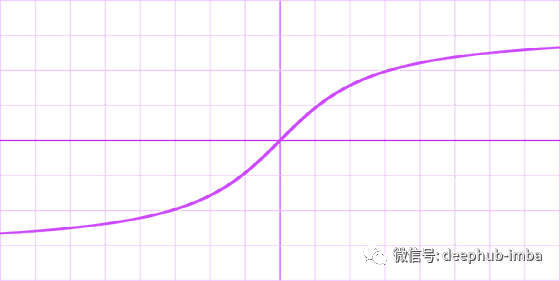
公式
导数
Softplus
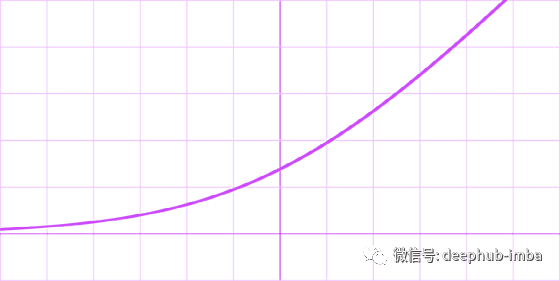
公式
导数
Rectified linear unit (ReLU) (ReLU6)

公式

导数

Exponential linear unit (ELU)
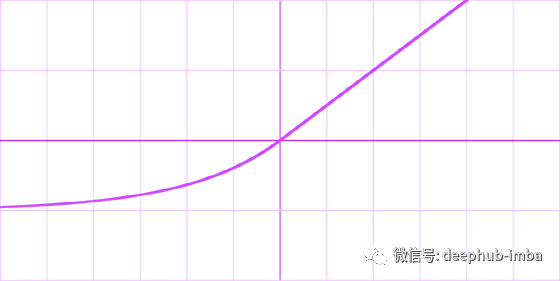
公式
导数
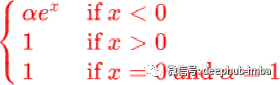
Gaussian Error Linear Unit (GELU)
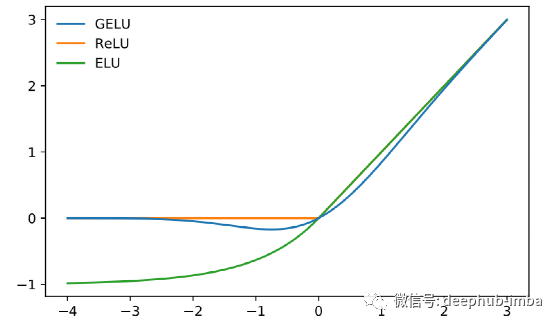
公式

导数

Scaled exponential linear unit (SELU)
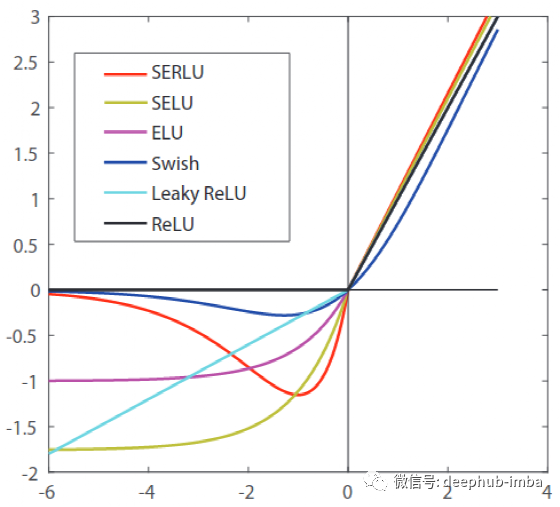
公式

导数

Mish
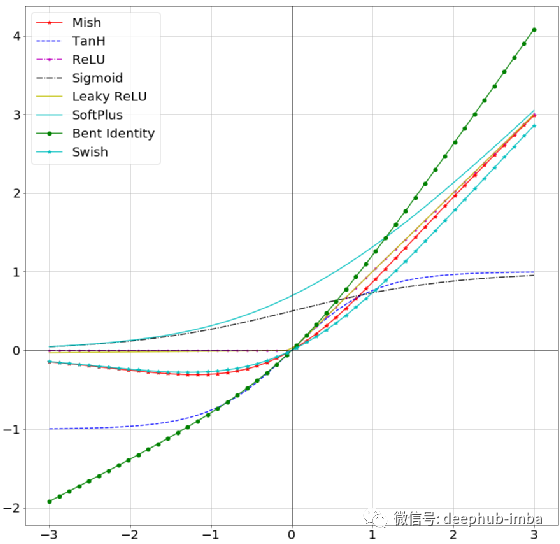
公式
导数
Leaky rectified linear unit (Leaky ReLU)
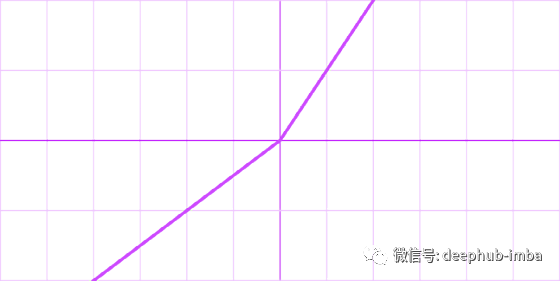
公式
导数

Parametric rectified linear unit (PReLU)
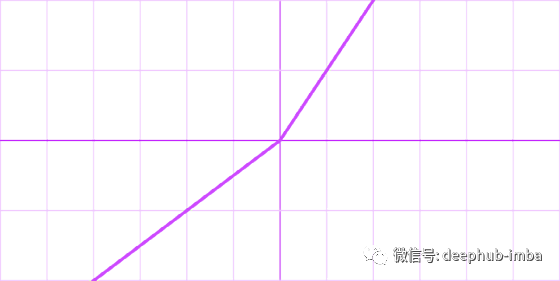
公式
导数

Parametric Exponential Linear Unit (PELU)
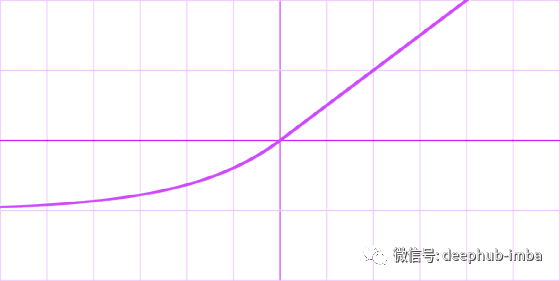
公式
导数
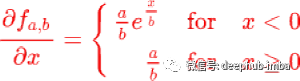
S-shaped rectified linear activation unit (SReLU)
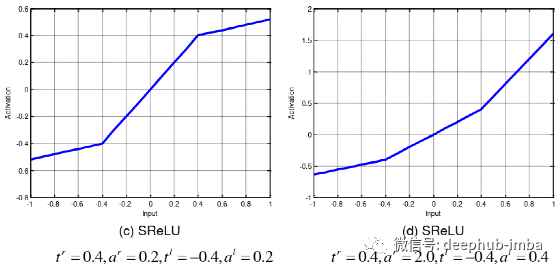
公式

导数
Bipolar rectified linear unit (BReLU)
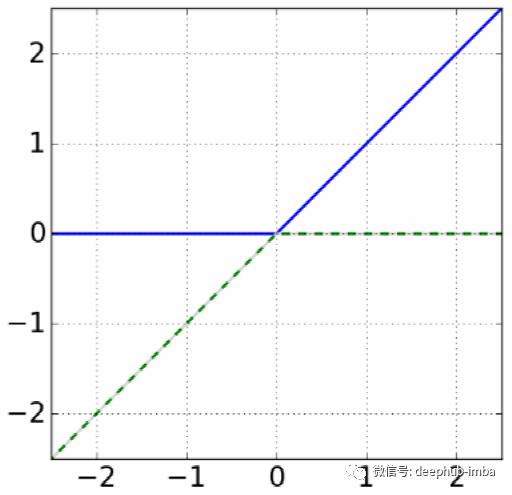
公式

导数
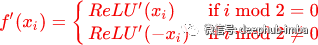
Randomized leaky rectified linear unit (RReLU)
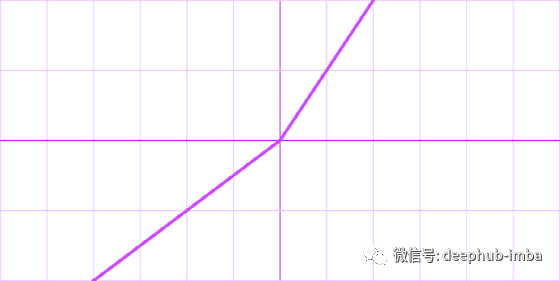
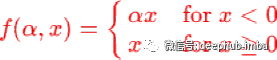

Sigmoid linear unit (SiLU) or Swish
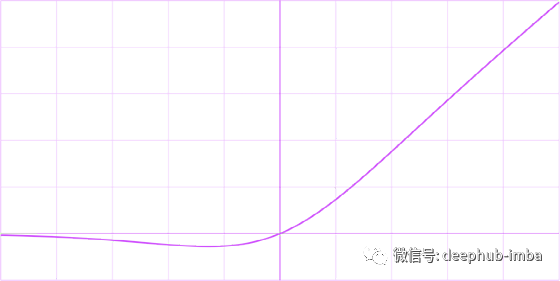

Gaussian
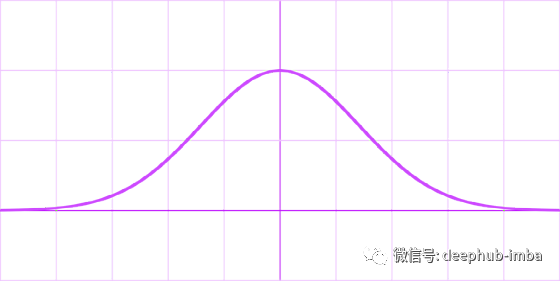
Growing Cosine Unit (GCU)
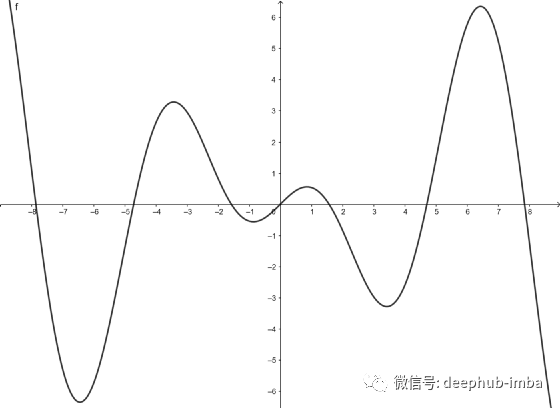
Shifted Quadratic Unit (SQU)
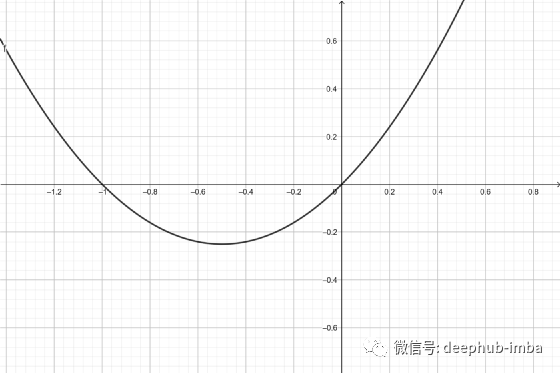


Non-Monotonic Cubic Unit (NCU)
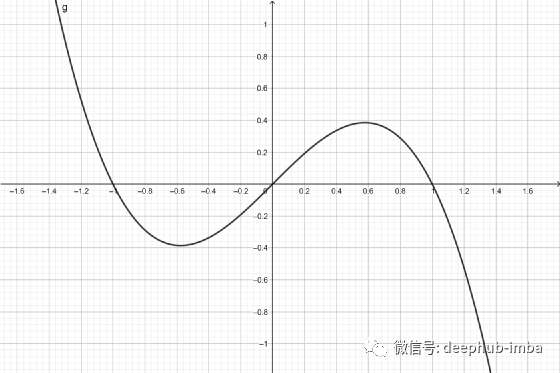

Shifted Sinc Unit (SSU)
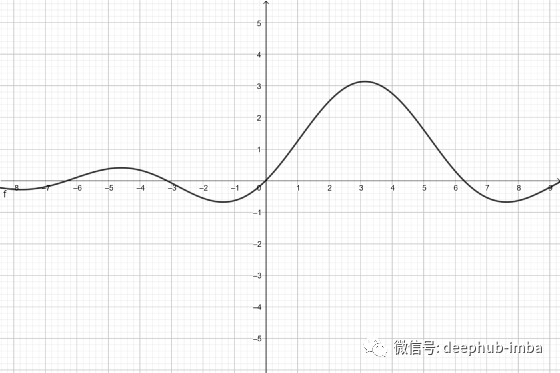
没有提供导数公式,参考论文:https://arxiv.org/pdf/2111.04020.pdf。
Decaying Sine Unit (DSU)
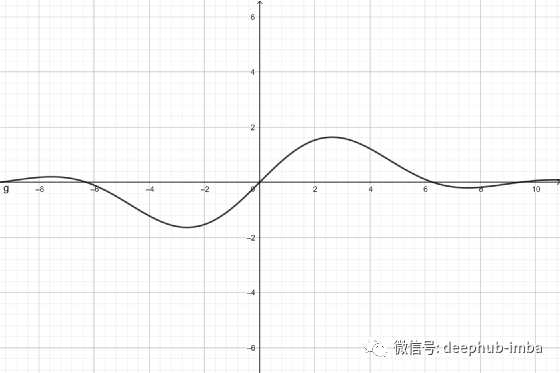

没有提供导数公式,请参考论文:https://arxiv.org/pdf/2111.04020.pdf
Phish
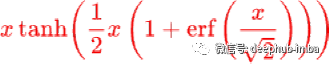
没有提供导数公式,请参考论文:https://www.techrxiv.org/ndownloader/files/33227273/2
SQ-RBF
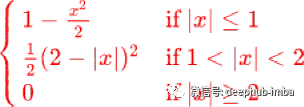
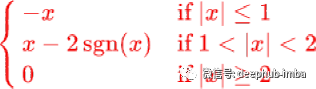
Inverse square root unit (ISRU)
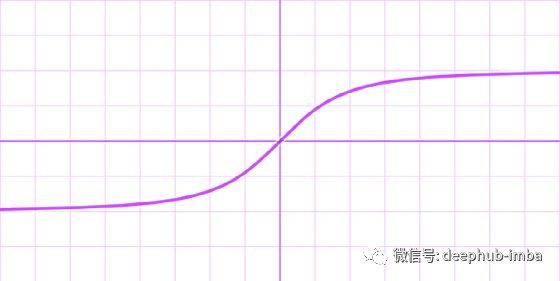


Square nonlinearity (SQNL)
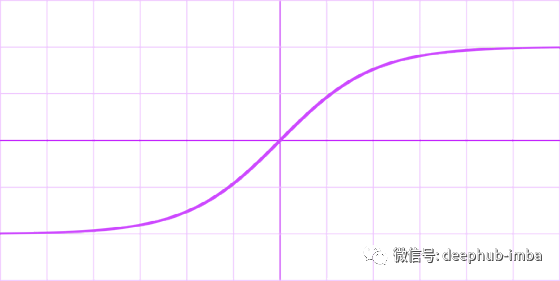
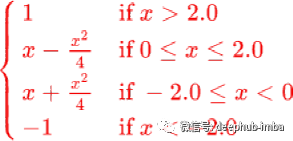
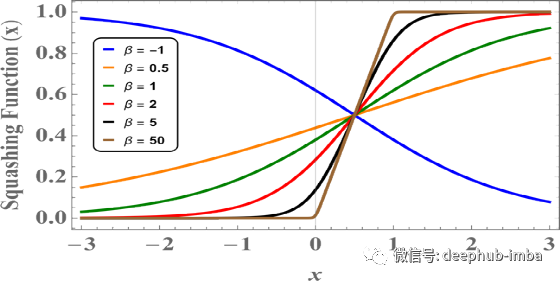
Sigmoid shrinkage
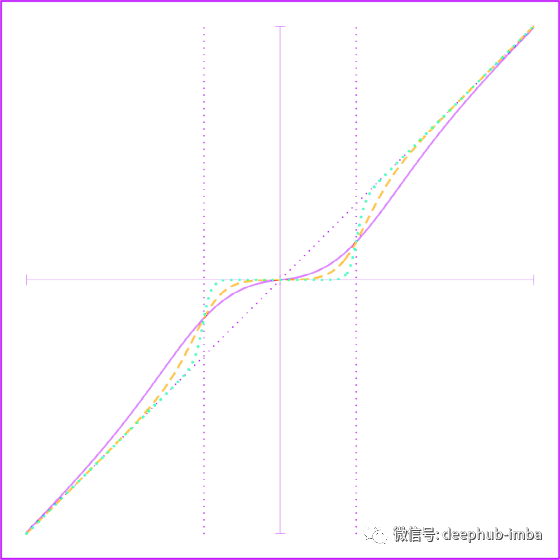
“Squashing functions”
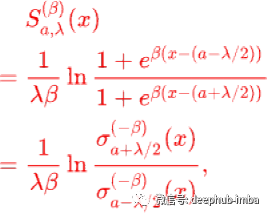

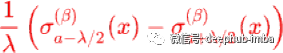
Maxout
该函数导数为正负 无限
Bent Identity
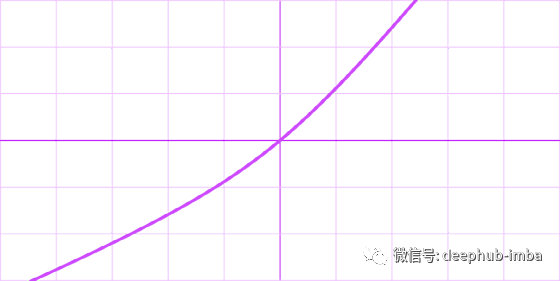


Sinusoid
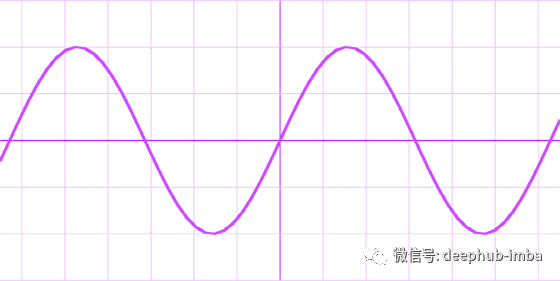
Sinc (taming the waves)
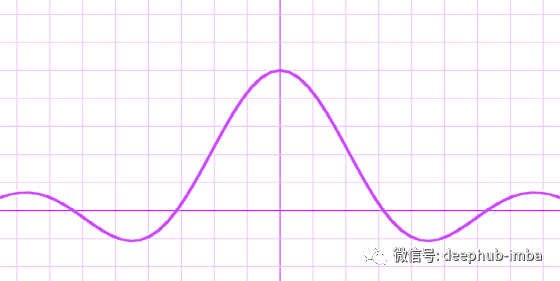


ArSinH
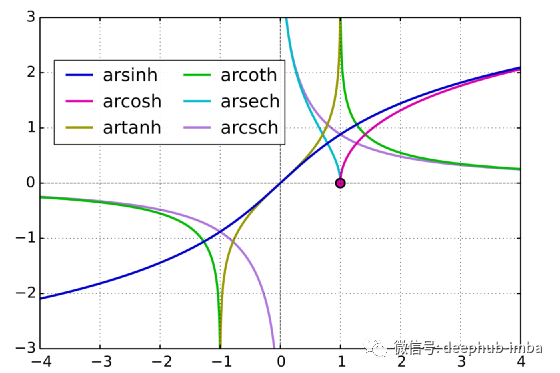

Soft Clipping (goldilocks)


Piecewise Linear Unit (PLU)
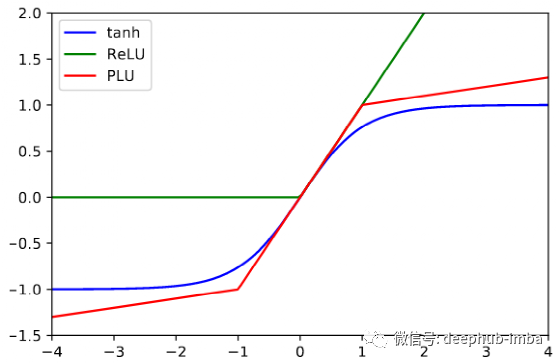
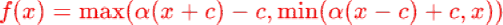

Adaptive piecewise linear (APL)
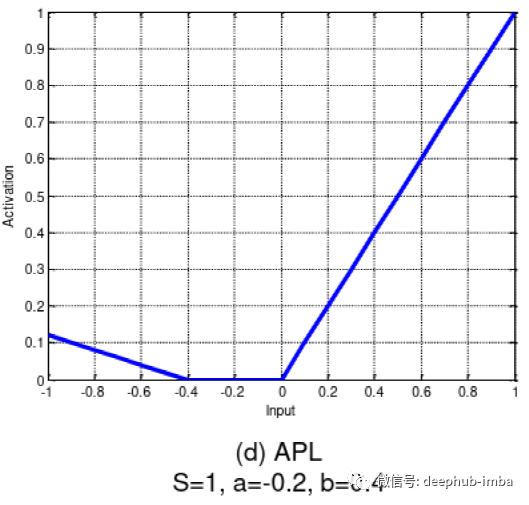
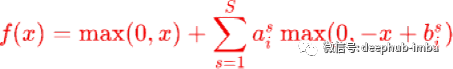

Inverse Cubic


Soft Exponential
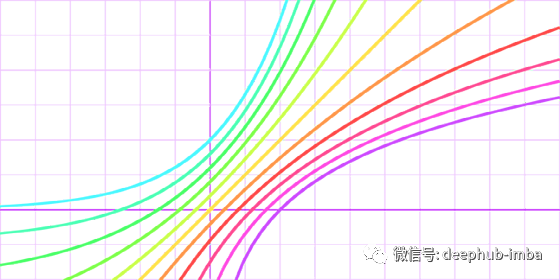
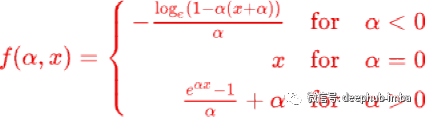
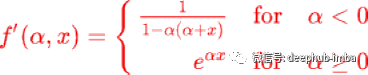
LeCun hyperbolic tangent (42?)
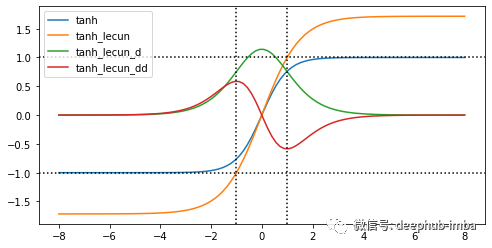
https://avoid.overfit.cn/post/18eb8aef0eb740c2a6c49bc43b833d1f
https://blog.csdn.net/deephub/article/details/124423141
===========================================
https://zhuanlan.zhihu.com/p/516728106
1.激活函数使用频率
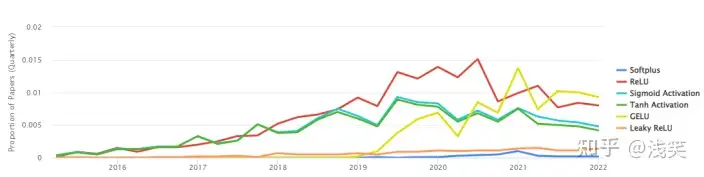
2. 激活函数类型
(1) RELU类激活函数对比
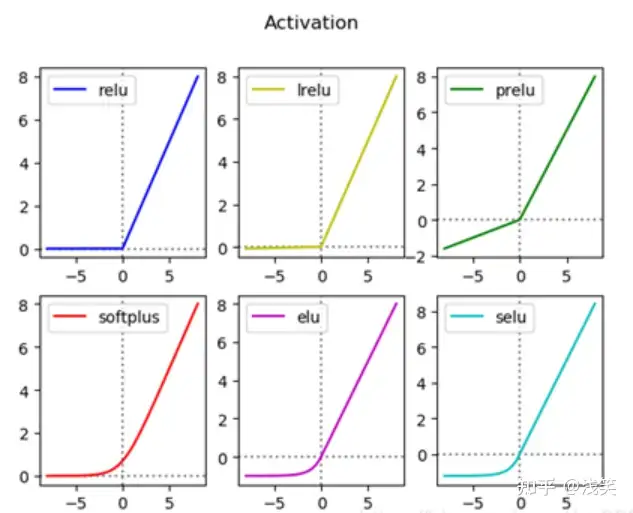
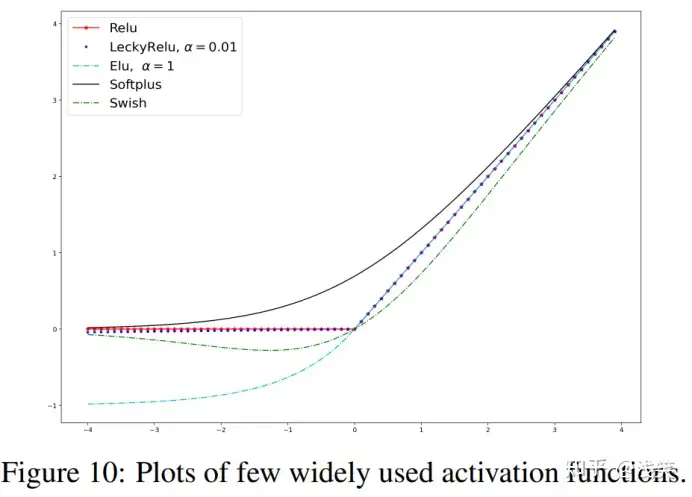
(2) S形激活函数对比
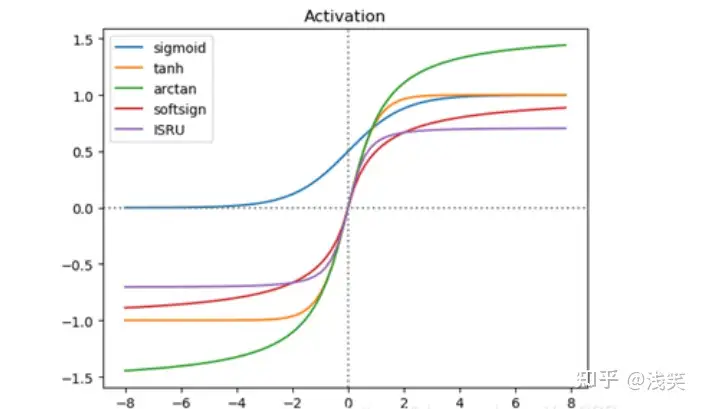
3. 激活函数公式与曲线
(后期会不定期进行更新)
(1) 恒等函数
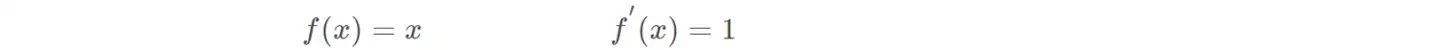
(2)单位阶跃函数

(3)sigmoid函数/逻辑函数
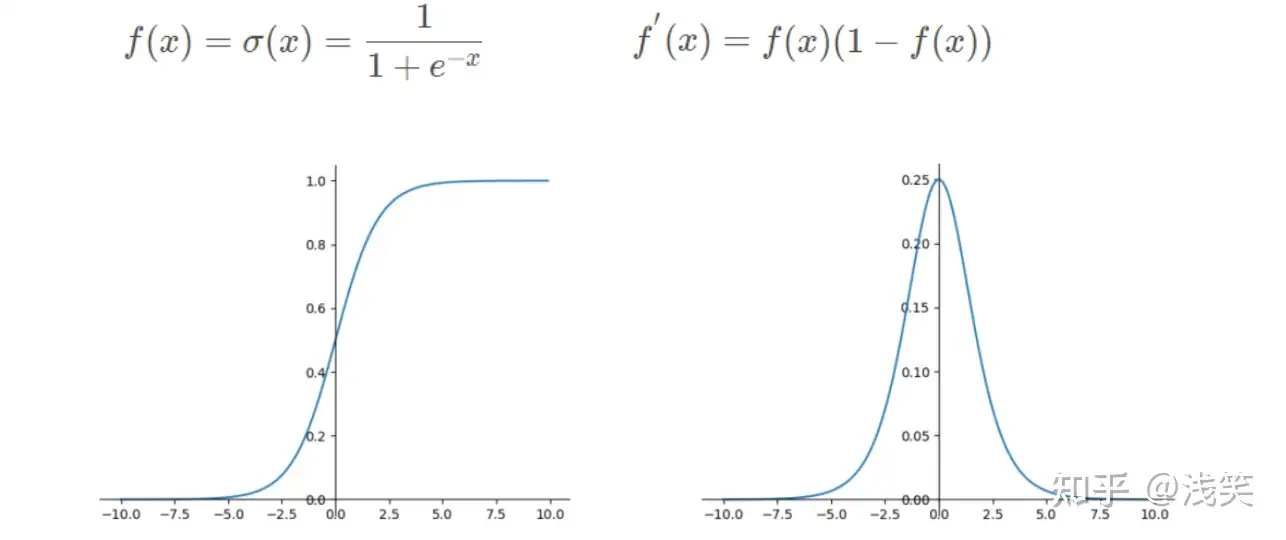
(4)hard_sigmoid
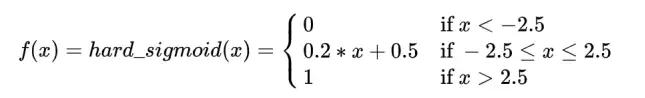
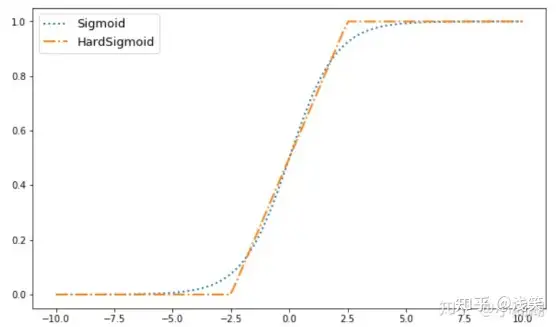
(5)tanh函数/双曲正切函数
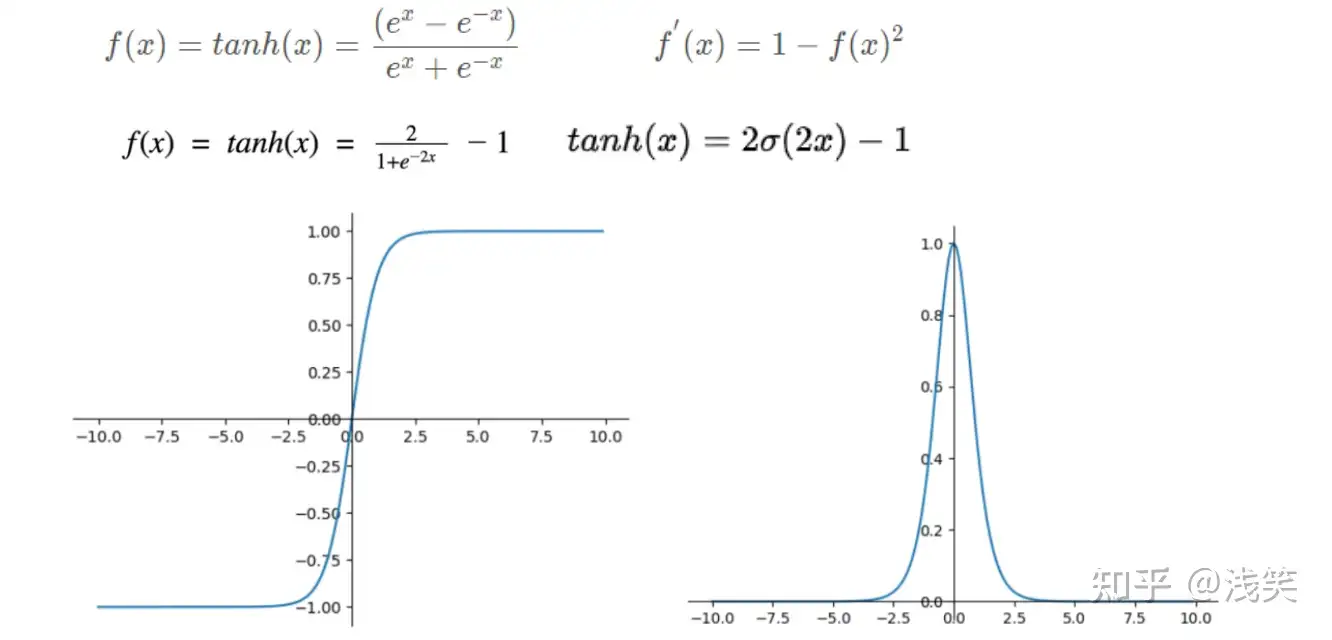
(6)反正切函数
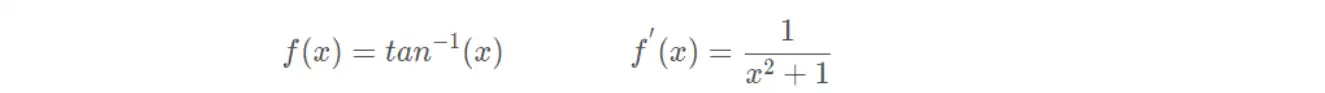
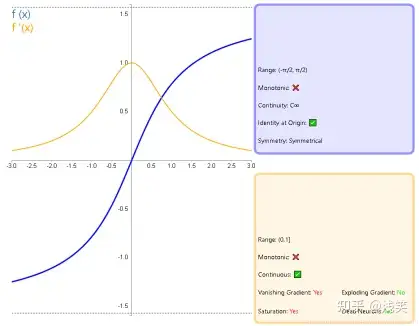
(7)Softsign函数
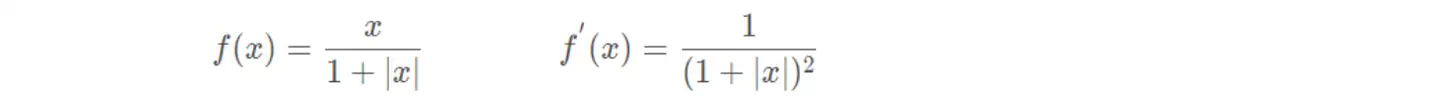
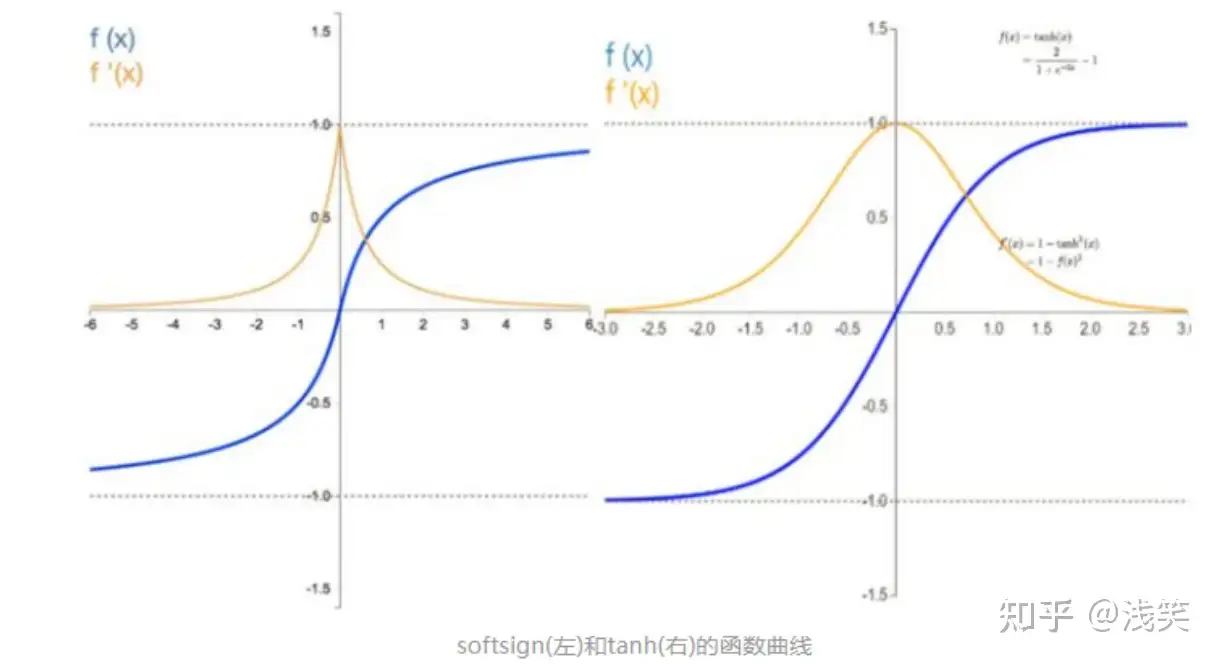
(8)反平方根函数(ISRU)
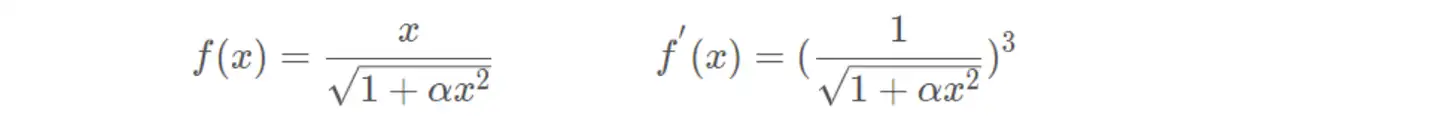
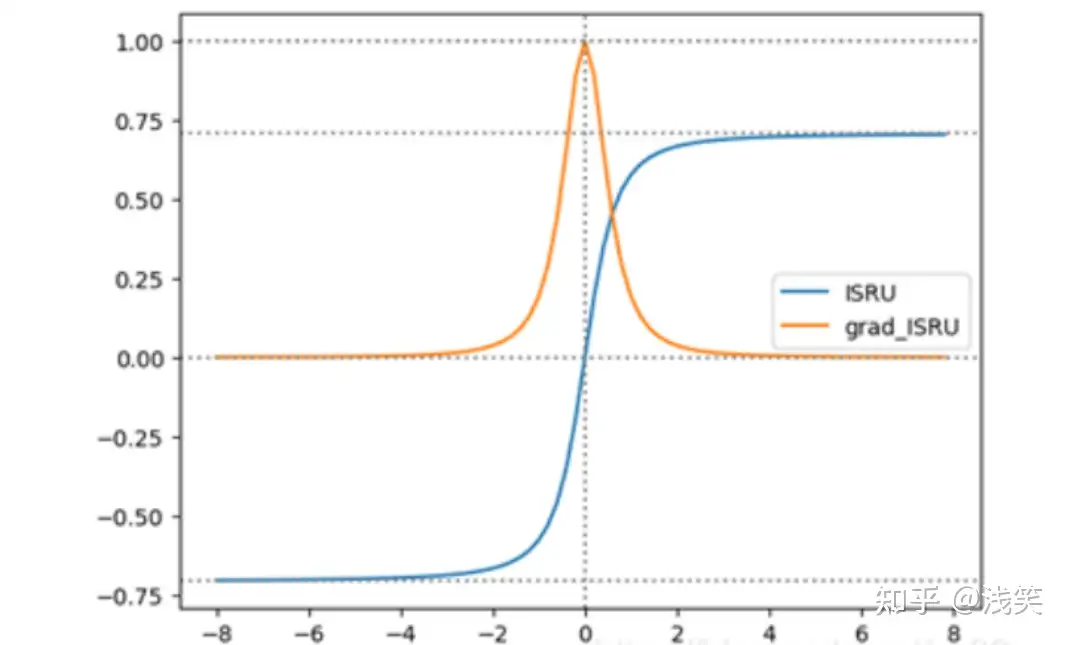
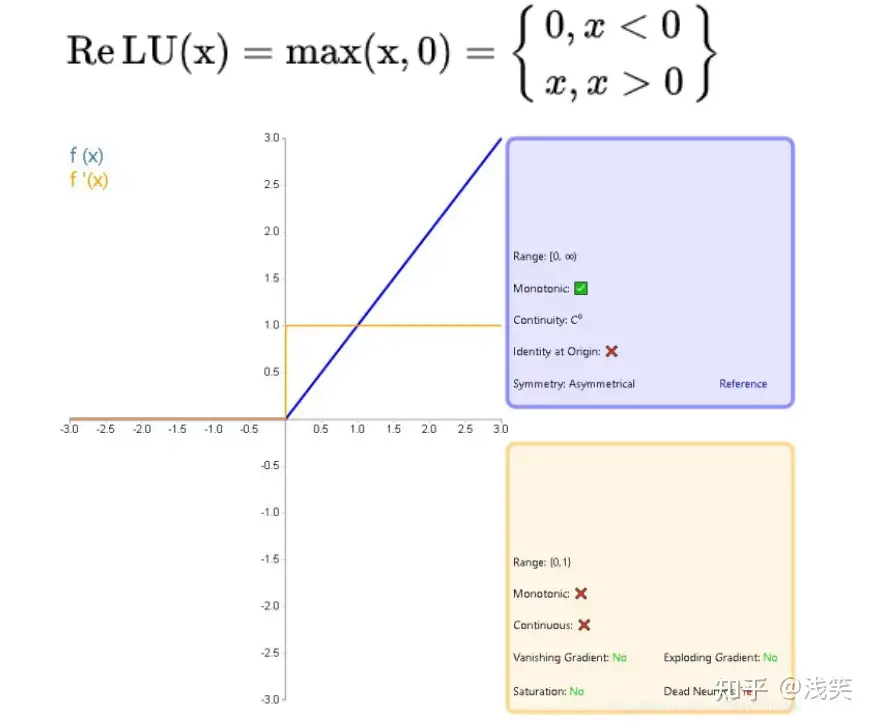
(9)线性整流函数(ReLU)
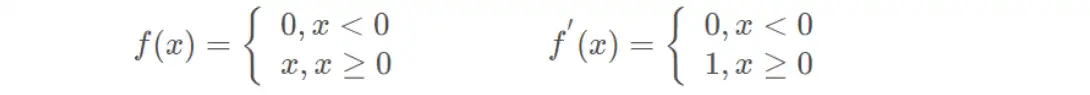
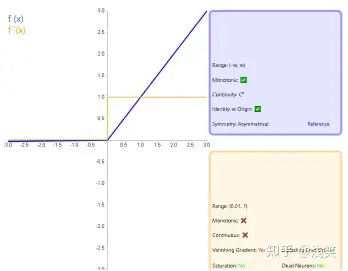
(10) 带泄露线性整流函数(Leaky ReLU)
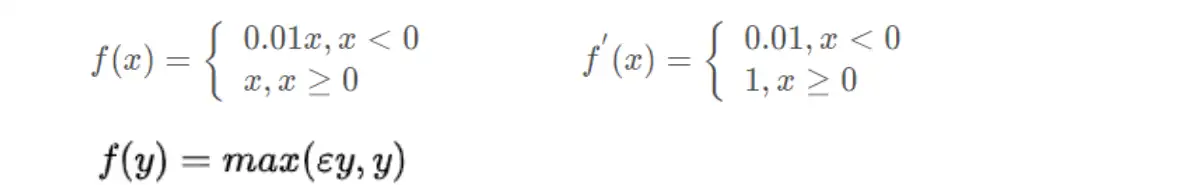
(11)参数化线性整流函数(PReLU)
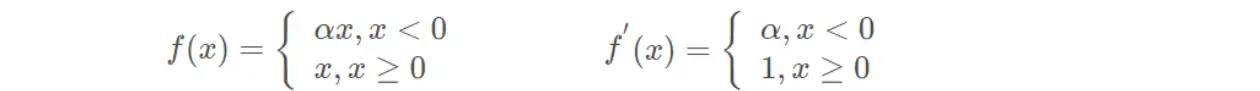
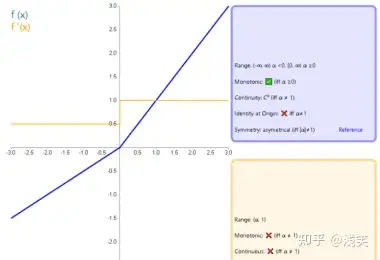
(12)带泄露随机线性整流函数(RReLU)
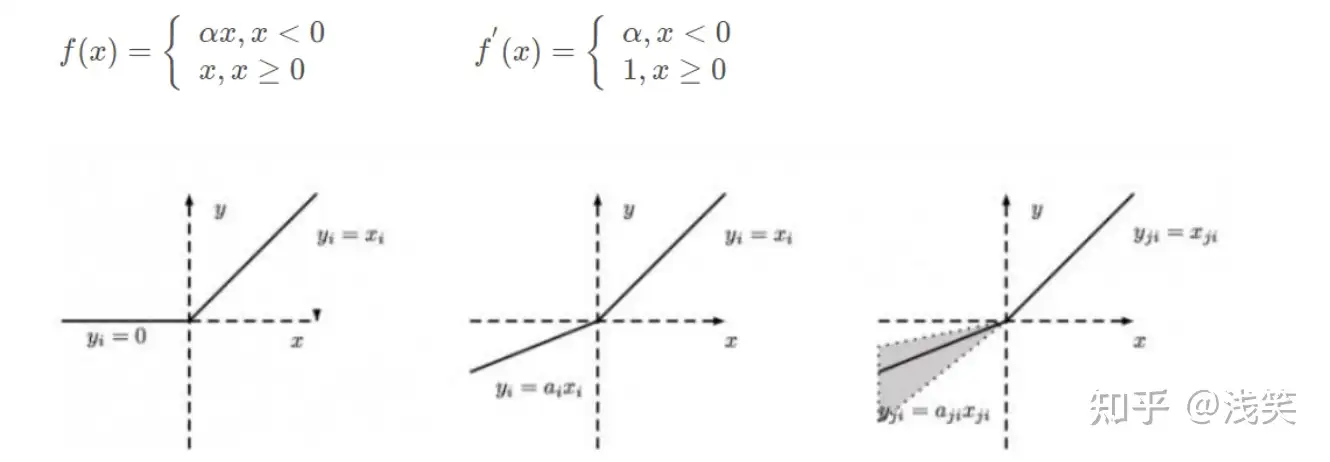
(13)指数线性函数(ELU)
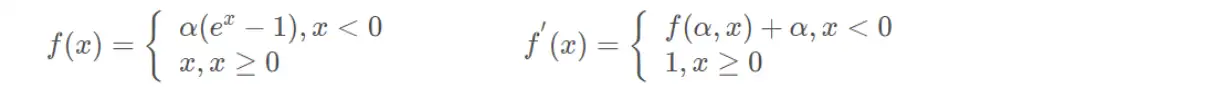
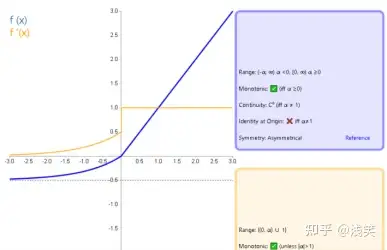
(14)扩展指数线性函数(SELU)
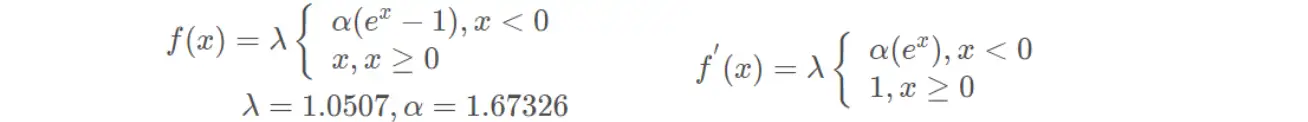
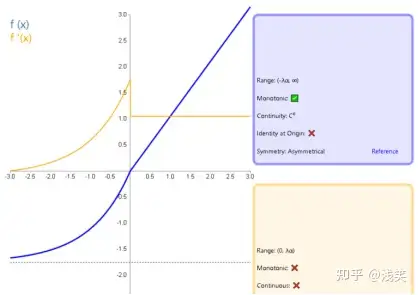
(15)S型线性整流激活函数(SReLU)
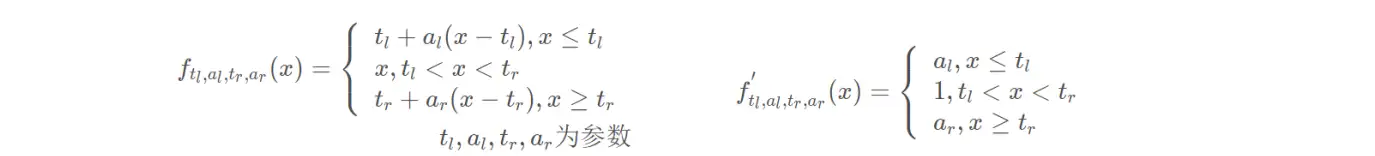
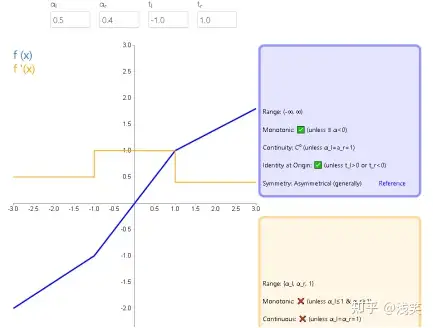
(16)反平方根线性函数(ISRLU)
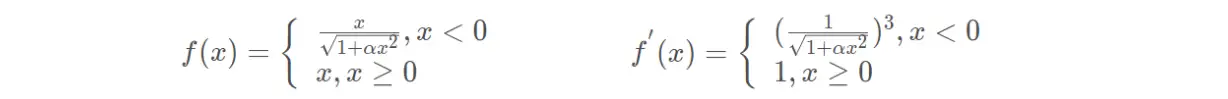
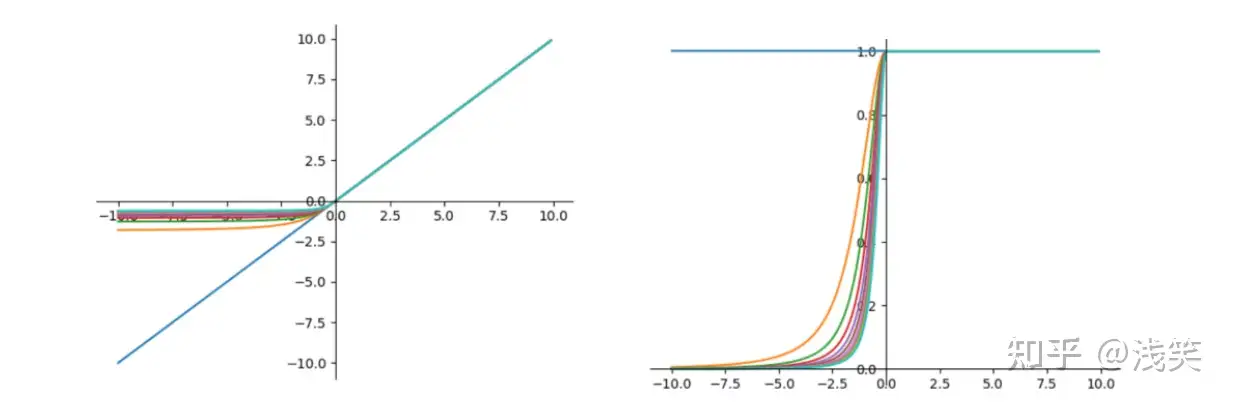
(17)自适应分段线性函数(APL)
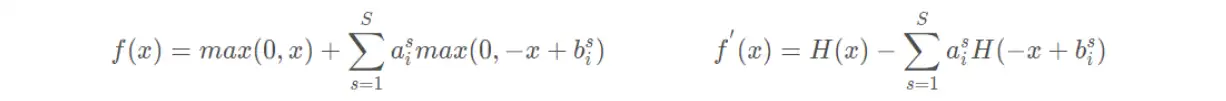
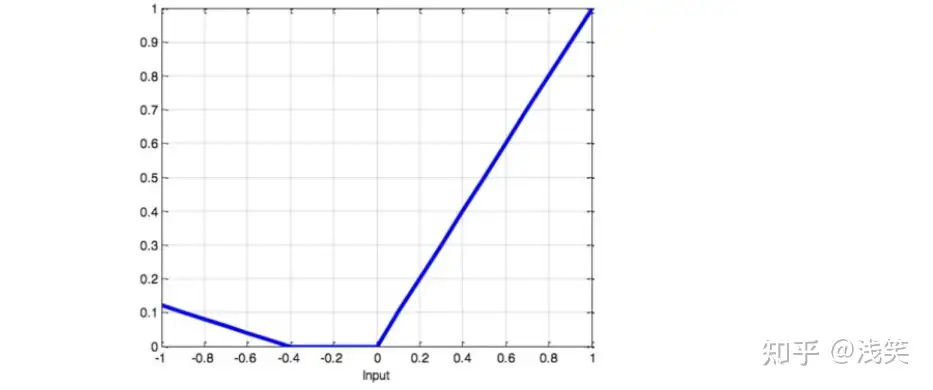
(18)SoftPlus函数

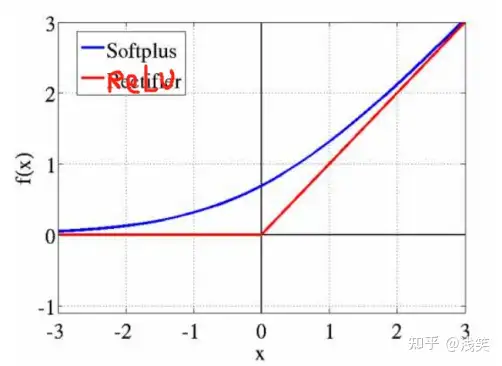
(19)弯曲恒等函数
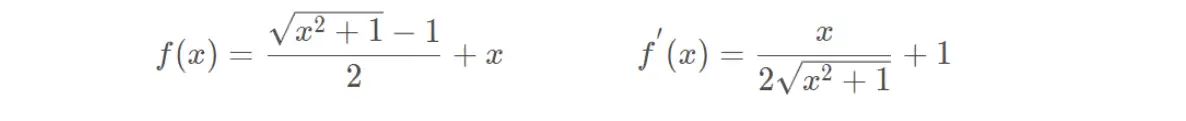
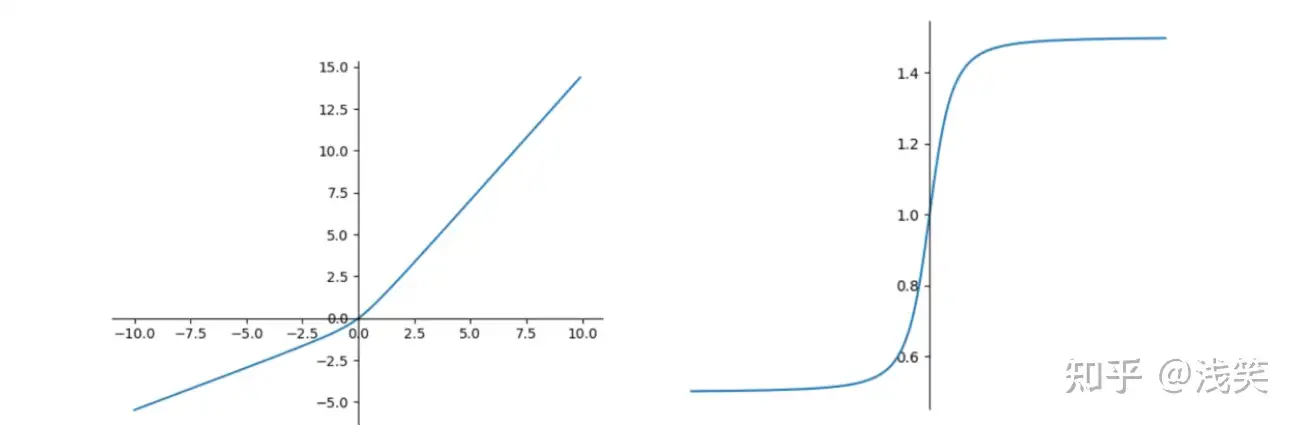
(20)SigmoidWeightedLinerUnit(SiLU)
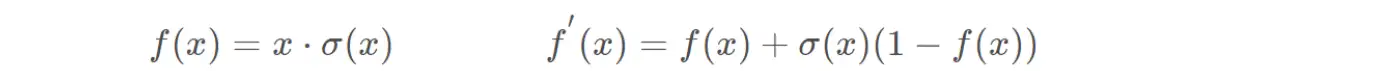
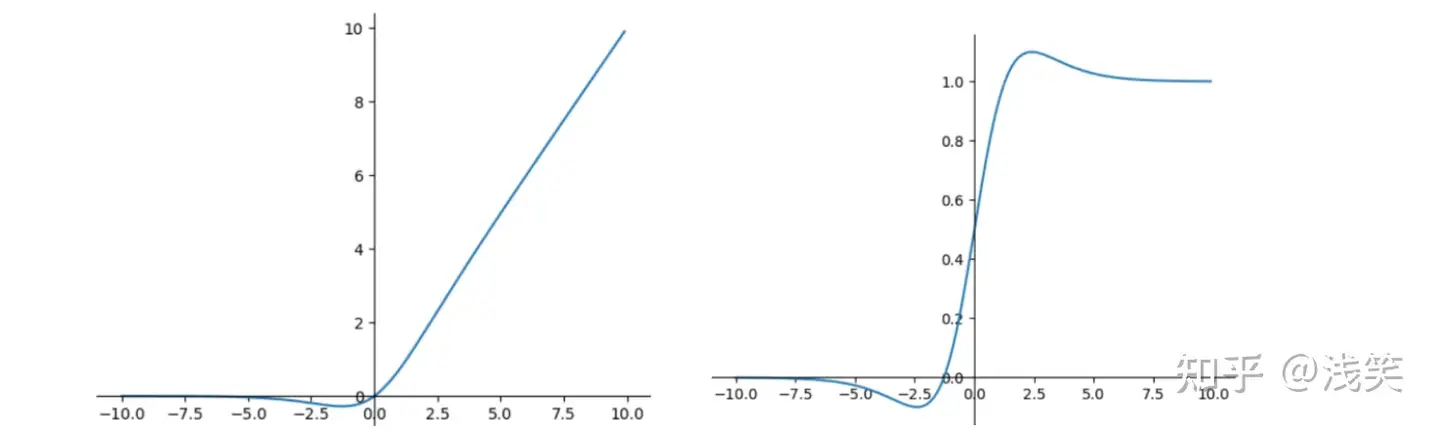
(21)SoftExponential
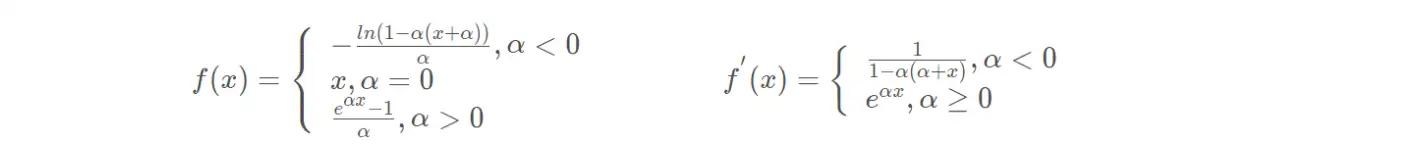
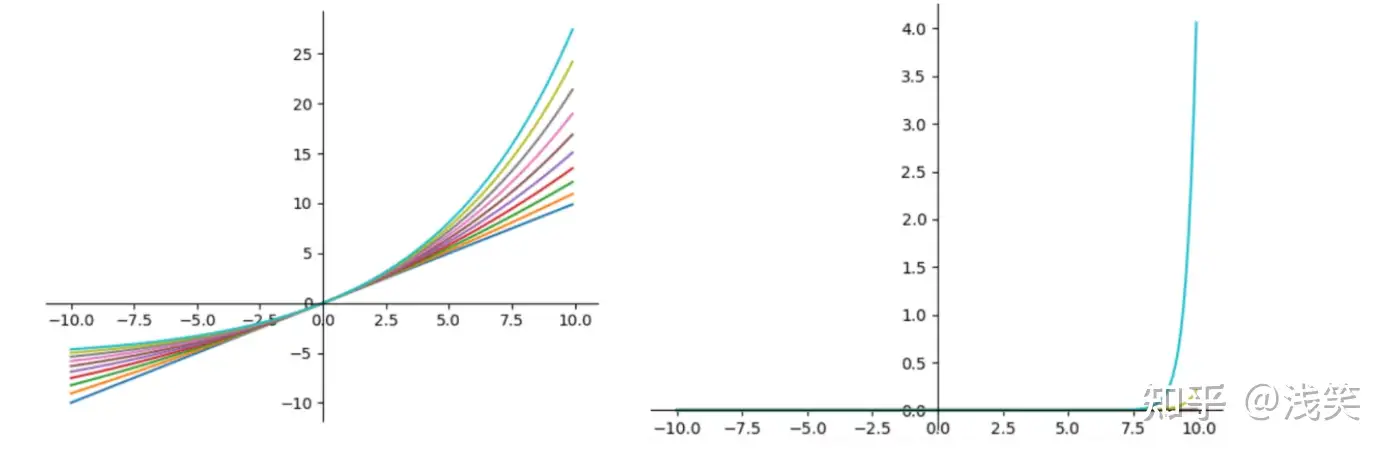
(22)正弦函数
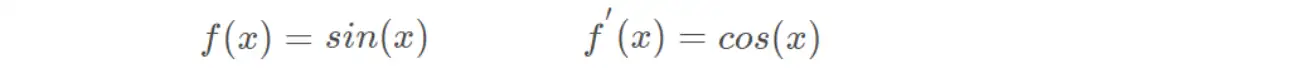
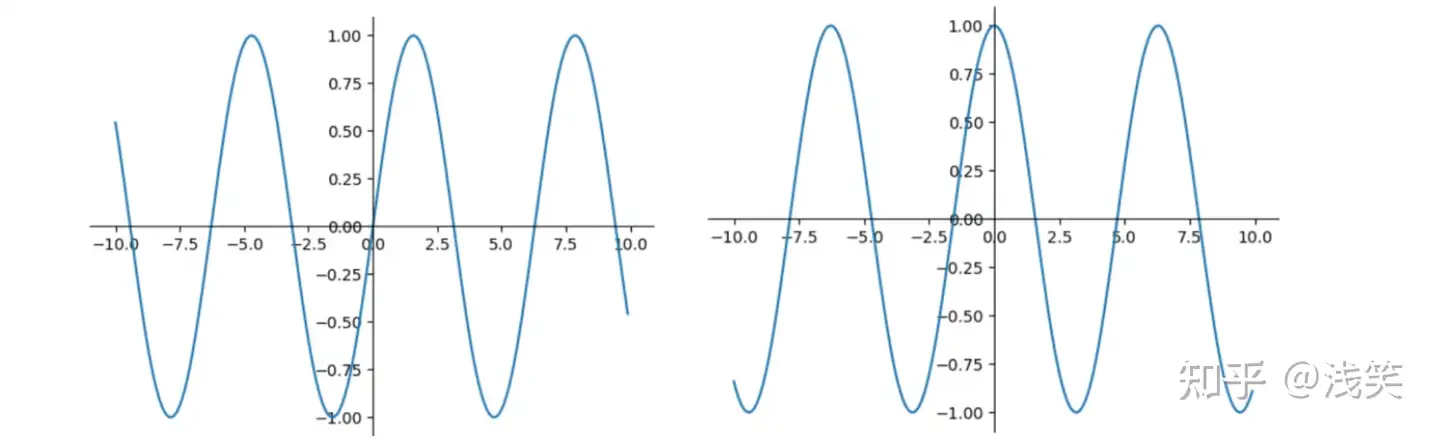
(23)Sinc函数
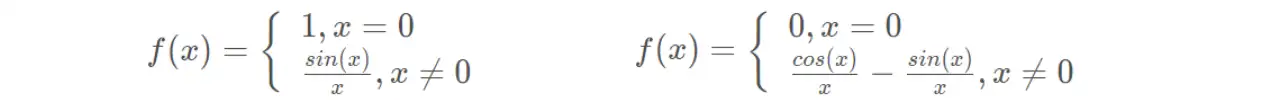
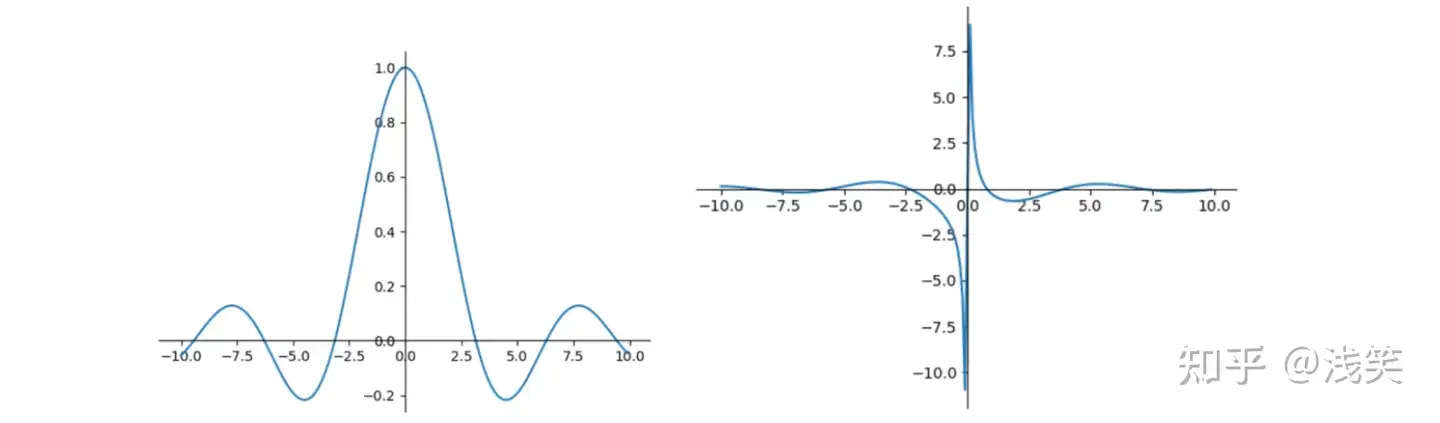
(24)高斯函数
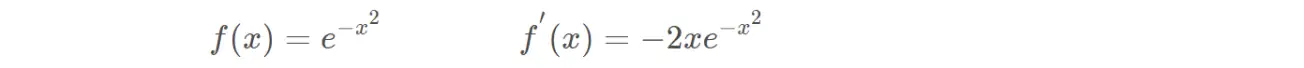
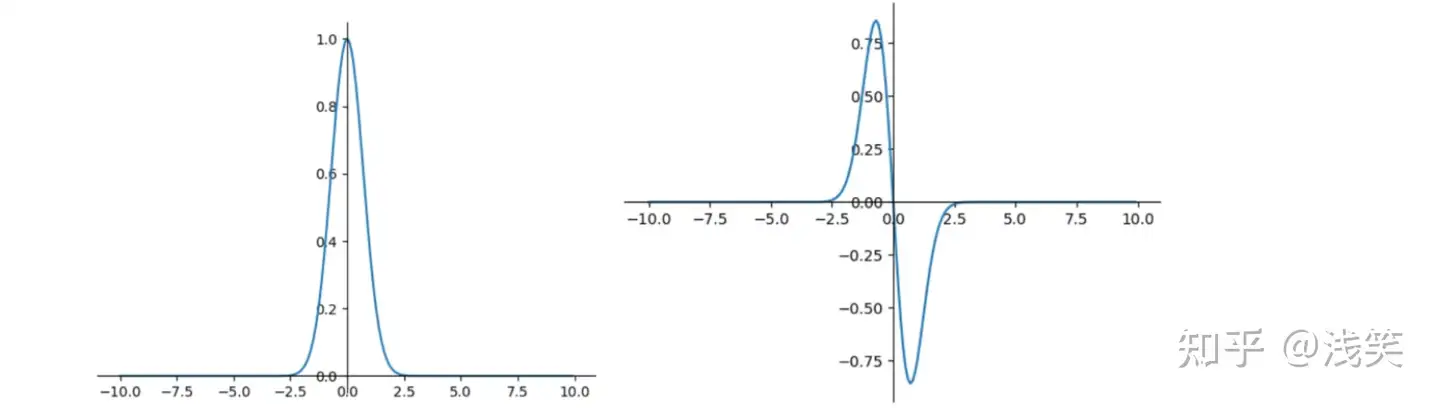
(25)自门控激活函数(swish)
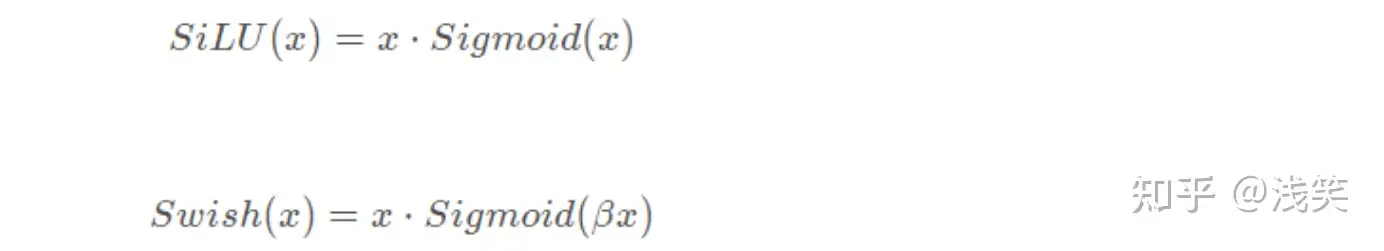
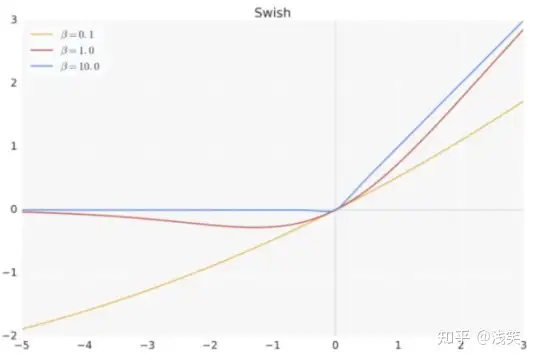
(26)hard-Swish
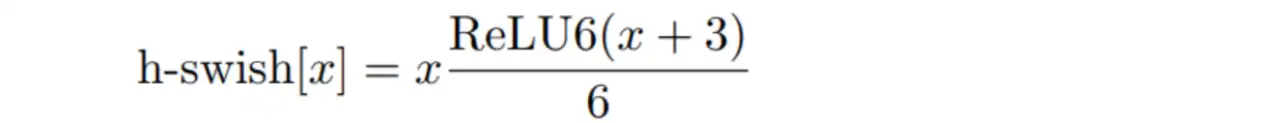
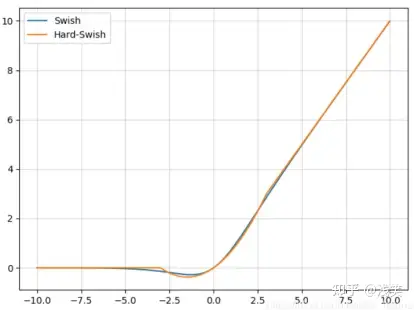
(27)Mish
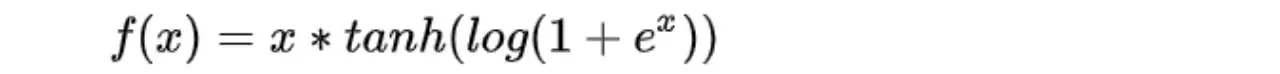
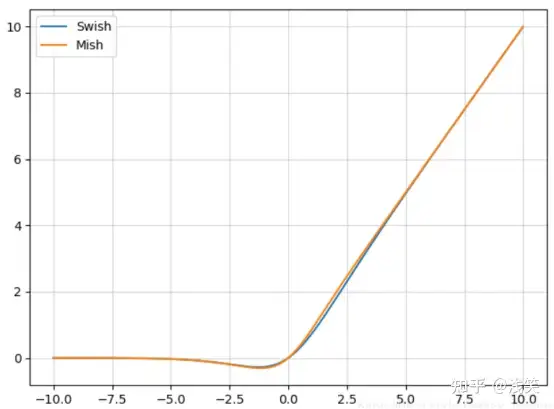
(28)ReLU6
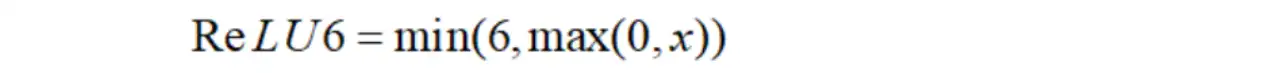
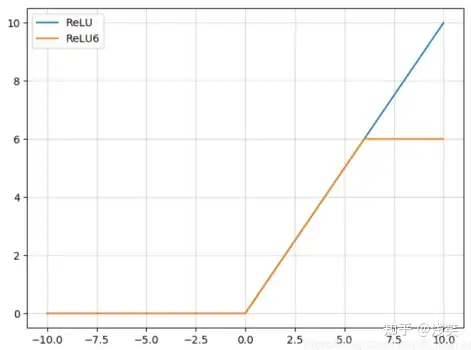
(29)Maxout
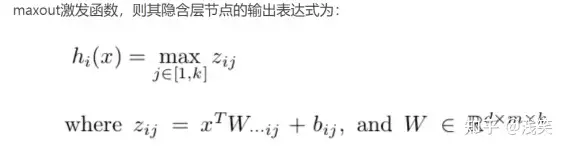
(30)FReLU
(31)ACONC
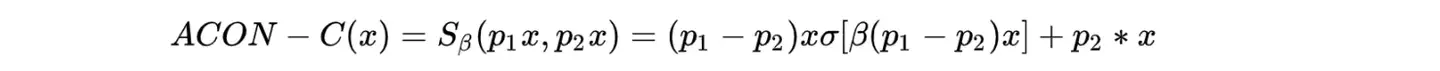
(32)GELU
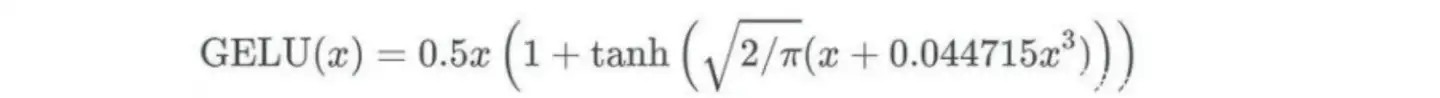
===========================================
https://blog.csdn.net/GrayOnDream/article/details/102955297
===========================================


 浙公网安备 33010602011771号
浙公网安备 33010602011771号