深入理解激活函数
深入理解激活函数
激活函数对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。如图,在神经元中,输入(inputs )通过加权,求和后,还被作用在一个函数上,这个函数就是激活函数。
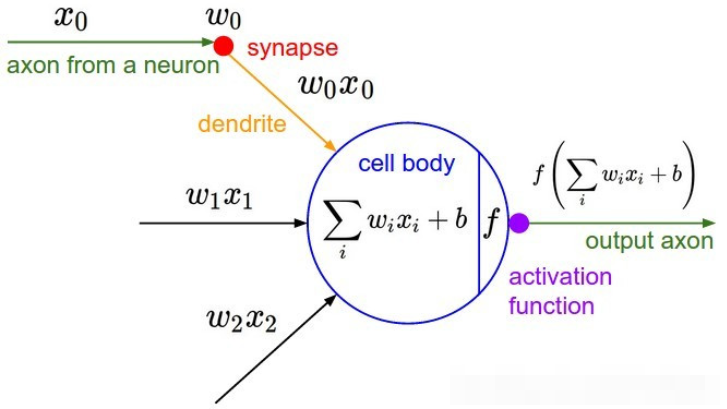
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。
如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
原文链接:https://blog.csdn.net/u013705056/article/details/111373841
如果使用线性激活函数,那么输入跟输出之间的关系为线性的,无论神经网络有多少层都是线性组合。
使用非线性激活函数是为了增加神经网络模型的非线性因素,以便使网络更加强大,增加它的能力,使它可以学习复杂的事物,复杂的表单数据,以及表示输入输出之间非线性的复杂的任意函数映射。
输出层可能会使用线性激活函数,但在隐含层都使用非线性激活函数。
关于神经网络中的激活函数的作用,通常都是这样解释:不使用激活函数的话,神经网络的每层都只是做线性变换,多层输入叠加后也还是线性变换。因为线性模型的表达能力通常不够,所以这时候就体现了激活函数的作用了,激活函数可以引入非线性因素。
https://blog.csdn.net/weixin_44646390/article/details/127926813
1.激活函数定义?
在神经网络中,输入经过权值加权计算并求和之后,需要经过一个函数的作用,这个函数就是激活函数(Activation Function)。
2.激活函数的目的?
首先我们需要知道,如果在神经网络中不引入激活函数,那么在该网络中,每一层的输出都是上一层输入的线性函数,无论最终的神经网络有多少层,输出都是输入的线性组合;其一般也只能应用于线性分类问题中,例如非常典型的多层感知机。若想在非线性的问题中继续发挥神经网络的优势,则此时就需要通过添加激活函数来对每一层的输出做处理,引入非线性因素,使得神经网络可以逼近任意的非线性函数,进而使得添加了激活函数的神经网络可以在非线性领域继续发挥重要作用!
更进一步的,激活函数在神经网络中的应用,除了引入非线性表达能力,其在提高模型鲁棒性、缓解梯度消失问题、将特征输入映射到新的特征空间以及加速模型收敛等方面都有不同程度的改善作用!
正如绝大多数神经网络借助某种形式的梯度下降进行优化,激活函数需要是可微分(或者至少是几乎完全可微分的)。此外,复杂的激活函数也许产生一些梯度消失或爆炸的问题。
https://blog.csdn.net/caip12999203000/article/details/127067360

https://blog.csdn.net/weixin_39910711/article/details/114849349
==========================================
激活函数类型
wiki中给出了激活函数的类型,这里略做归纳
. ldentity function(恒等函数)
. Step function(阶跃函数)
Sigmoidal function (S形函数)
. Ramp function (斜坡函数)
Binary 和 Bipolar的区别应该是 Binary(单位)对应值为0或1,Bipolar(两极)对应值为-1或1
激活函数的一些特性
非线性(Nonlinear) 当激活函数是非线性的,那么一个两层神经网络也证明是一个通用近似函数通用近似理论。而恒等激活函数则无法满足这一特性,当多层网络的每一层都是恒等激活函数时,该网络实质等同于一个单层网络。
输出值域(Range) 若激活函数的值域是有限的,因为对权重的更新影响有限,所以基于梯度的训练方法更稳定。若值域是无限的,因为大多数情况下权重更新更明显,所以训练通常更有效,通常需要设定较小的学习率。
连续可微(Continuously differentiable) 通常情况下,当激活函数连续可微,则可以用基于梯度的优化方法。(也有例外,如ReLU函数虽不是连续可微,使用梯度优化也存在一些问题,如ReLU存在由于梯度过大或学习率过大而导致某个神经元输出小于O,从而使得该神经元输出始终是O,并且无法对与其相连的神经元参数进行更新,相当于该神经元进入了“休眠”状态,参考深度学习中,使用relu存在梯度过大导致神经元“死
亡”,怎么理解?·知乎,但RelLU还是可以使用梯度优化的。)二值阶跃函数在0处不可微,并且在其他地方的导数是零,所以梯度优化方法不适用于该激活函数。
单调(Monotonic) 当激活函数为单调函数时,单层模型的误差曲面一定是凸面。即对应的误差函数是凸函数,求得的最小值一定是全局最小值。
一阶导单调(Smooth functions with a monotonic derivative) 通常情况下,这些函数表现更好。
原点近似恒等函数(Approximates identity near the origin) 若激活函数有这一特性,神经网络在随机初始化较小的权重时学习更高效。若激活函数不具备这一特性,初始化权重时必须特别小心。参考machine learning - Why activation functions that approximate the identitnear origin are preferable? - Cross Validated
https://wenku.baidu.com/view/c38c487dbd23482fb4daa58da0116c175f0e1e2a.html?_wkts_=1690274677596&bdQuery=softExponential
==========================================
==========================================
==========================================
==========================================


 浙公网安备 33010602011771号
浙公网安备 33010602011771号