Informer模型与基础学习
https://blog.csdn.net/weixin_44790306/article/details/124064177
摘要
本周一是对Informer论文的阅读,其关注的问题依然是长时间序列预测问题。也是从self-attention 机制的缺陷出发,做了一些优化于改进工作,像ProbSparse self-attention,self-attention蒸馏机制,生成式 Decoder,其中还有比较关键的就是在LSTF问题中统一了输入表示。
二是关于pytorch基础部分学习,如何去做一个完整网络模型的训练套路,基本步骤是:准备数据,加载数据(DataLoader的使用),准备创建好的模型,设置损失函数,设置优化器,开始训练过程,测试训练模型。
文献阅读
一. Informer: 一个基于Transformer改进的高效的长时间序列预测模型
作者:周浩义、张尚航、彭洁琪、张帅
单位:北京航空航天大学
论文链接地址: Informer长时间预测模型
代码地址:源码地址
1.1 论文摘要
对于长序列时间预测一直是研究的热点,随着预测序列长度增加,预测难度越来越高,LSTF需要模型提高预测能力,本文设计了一个高效的基于 Transformer 的 LSTF 模型,名为 Informer。informer模型成功地提高LSTF问题的预测能力,验证了类Transformer模型的潜在价值;Informer针对Transformer上的三大问题:二次时间复杂度,高内存消耗,Decoder逐步推理,制定提出解决方案:ProbSparse Self-Attention Mechanism ,自注意力蒸馏(self-attention distilling),生成式解码器(the generative style decoder)。
1.2 研究内容
Self-Attention Mechanism的计算、内存和架构效率成为Transformer应用解决LSTF问题的瓶颈。Transformer模型主要存在下面三个问题:
self-attention机制的二次计算复杂度问题:self-attention机制的点积操作使每层的时间复杂度和内存使用量为 O(L^2) 。
高内存使用量问题:对长序列输入进行堆叠时,J个encoder-decoder层的堆栈使总内存使用量为 O(J *L^2) ,这限制了模型在接收长序列输入时的可伸缩性。
预测长输出时速度骤降:原始 Transformer 的动态解码操作导致 step by step inference(逐步推理)的速度如同基于 RNN 的模型一样慢。
因此,本论文研究Transformer是否可以提高计算、内存和架构效率,以及保持更高的预测能力?之前也有许多改进的Transformer类模型,但都只是局限于解决上述第一个问题,而本文可以解决上述的三个问题。
Informer在Transformer基础上提出了三点改进:
提出了ProbSparse self-attention机制,时间复杂度为 O(LlogL) 【降低了常规 Self-Attention 计算复杂度和空间复杂度】;
提出了self-attention蒸馏机制来缩短每一层的输入序列长度,序列长度短了,计算量和存储量自然就下来了【使用自注意蒸馏技术缩短每一层的输入序列长度,降低了 J 个堆叠层的内存使用量】;
提出了生成式的decoder机制,在预测序列(也包括inference阶段)时一步得到结果,而不是step-by-step,直接将预测时间复杂度由 O(N) 降到了 O(1) 【改变解码方式直接一步输出结果】。
1.3 Informer模型架构
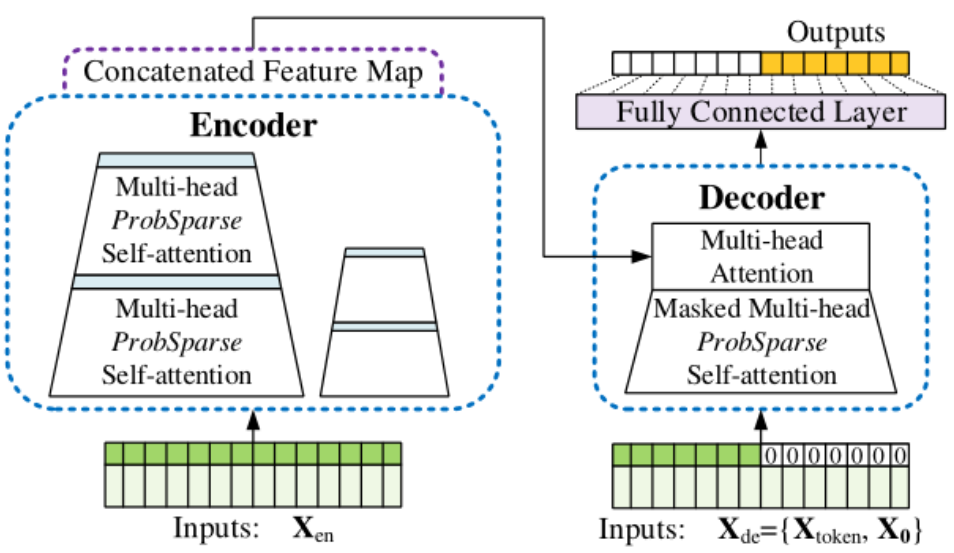
左侧是Encoder部分,它接收超长的输入数据(绿色部分)。然后将传统的Self-Attention层替换为本文提出的ProbSpare Self-Attention层。蓝色的部分是Self-Attention distilling操作来进行特征压缩。Encoder模块通过堆叠上述的两个操作来提高算法的鲁棒性。右侧是Decoder部分,它接收一系列的长序列输入,并将预测目标位置填充为0,再通过经过Mask的Attention层,最后一步生成预测输出(橙色部分)。
1.3.1 预备知识
1.3.1 .1 LSTF问题定义
在具有固定窗口大小的滚动预测设置下,我们有:
在时间点t的输入,
在这里插入图片描述
Lx表示当前输入序列的长度,这里面的每个点,都是一个dx维度的向量。
输出是预测对应的序列 :
在这里插入图片描述
Ly表示当前输出序列的长度,这里的每个点,都是一个dy维度的向量。
相比以前的工作, L S T F LSTF LSTF 问题鼓励更长的输出长度 Ly (并且特征维度不限于单变量情况 (即, d y > = 1 d_y>=1 dy>=1)。
1.3.1.2 Encoder-Decoder 体系结构
现有流行的模型设计为将输入表示 X t X^t Xt 编码成隐藏状态表示 H t H^t Ht ,并将输出表示 Y t Y^t Yt 从隐藏状态 H t = h 1 t , … … , h L k t H^t = {h_1^t,……,h_Lk^t} Ht=h1t,……,hLkt解码出来。这种预测设计一种名为“动态解码”的逐步过程,其中解码器根据前一状态 h k t h_k^t hkt和其他来自第 K K K 步的必要输出来计算新的隐藏状态 h k + 1 t h_{k+1}^t hk+1t,然后预测第 k + 1 k+1 k+1 个序列 y k + 1 t y_{k+1}^t yk+1t。
注意这里传统的“自回归解码”是背景知识,并不是Informer所采用的。
1.3.1.3 统一输入表示
基于 RNN 的模型不依赖于时间戳,通过循环结构本身就可以捕获时间序列模式;原始 Transformer 使用点乘自注意机制并采用时间戳作为位置信息编码。然而,在 LSTF 问题中,时序建模不仅需要用到局部时序信息,还需要层次时间戳(week, month, year)和不可知的时间戳(holidays, events)。常规的自注意机制很难直接适配,编码器和解码器之间的 query-key 不匹配会降低预测性能。因此,Informer 给出一个统一的输入表示如下图所示:
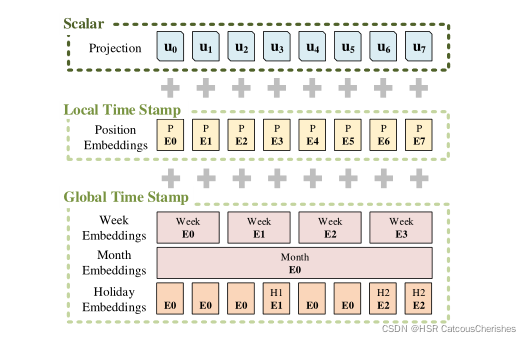
假设有 t t t个序列,输入 X t X^t Xt和 P P P 种类型的全局时间戳,输入表示后的特征维度是 d m o d e l d_{model} dmodel 。
如上图所示,输入的嵌入由三个独立的部分组成——标量投影、局部时间戳(Position)和全局时间戳(Minutes, Hours, Week, Month, Holiday 等):
局部时间戳:通过固定位置嵌入保存上下文信息,即原始 Transformer 的位置编码:
在这里插入图片描述
全局时间戳:使用可学习戳嵌入 S E ( p o s ) SE(pos) SE(pos)表示全局时间戳,其 vocab size 大小有限制(最多60个,即以每分钟为最细粒度)。即,自注意的相似性计算可以访问全局上下文,且计算消耗在长输入上也是可承受的。
对齐维度; 使用一维卷积滤波器(kernel width=3,stride=1)将标量上下文[ X i t X_i^t Xit]映射到 d m o d e l d_{model} dmodel 维的向量[ u i t u_i^t uit] 。
经过上述三步,可得到馈入模型的输入表示向量:
在这里插入图片描述
对于模型具体到底如何输入序列仍需要去进一步学习(待补充)
1.3.2 ProbSparse self-attention
ProbSparse Self-Attention用于解决self-attention点积计算的时间复杂度从 O ( L 2 ) O(L^2) O(L2)——优化至 O ( l ∗ l o g L ) O(l*logL) O(l∗logL)
通过采样 l o g L logL logL个点进行点积计算而不是选取整个 L L L进行点积:
ProbSparse Self-Attention 工作流程:
(1)为每个 query 都随机采样部分的 key,默认值为 5 ∗ l n L 5*lnL 5∗lnL ;
(2)计算每个 query 的稀疏性得分 M ( q i , k ) M(q_i,k) M(qi,k) ;
(3)选择稀疏性得分最高的 N 个 query ,N 默认值为 5 ∗ l n L 5*lnL 5∗lnL;
(4)只计算 N 个 query 和 key 的点积结果,进而得到 attention 结果;
(5)其余的 L-N 个 query 就不计算了,直接将 Self-Attention 层的输入取均值(mean(V))作为输出,这样可保证每个 ProbSparse Self-Attention 层的输入和输出序列长度都是 L L L。
所以整体的时间复杂度为 O ( L l n L ) O(Lln L) O(LlnL)。
这个机制只用在了self-attention中。在论文中,作者把提出的方法称为probsparse self-attention,在源代码中,也只用在了self-attention中,并没有用于cross-attention。
这个机制在有三角矩阵masking的情况下也不能用,因为在有masking的情况下,query和key的乘法数量本来就减少了。
因此,probsparse只能用于encoder的self-attention中,虽然论文中提出probsparse可以减少复杂度,但由于增加了排序的过程,不一定能减少计算时间,在一些数据长度本来就较少的情况下,可能会增加计算时间。
ProbSparse self-attention的核心思想:是找到某些重要的/稀疏的query,从而只计算这些query的attention值,来优化计算效率。
1.3.3 self-attention蒸馏机制
Encoder如下图所示:允许在内存使用限制下处理更长的序列输入。
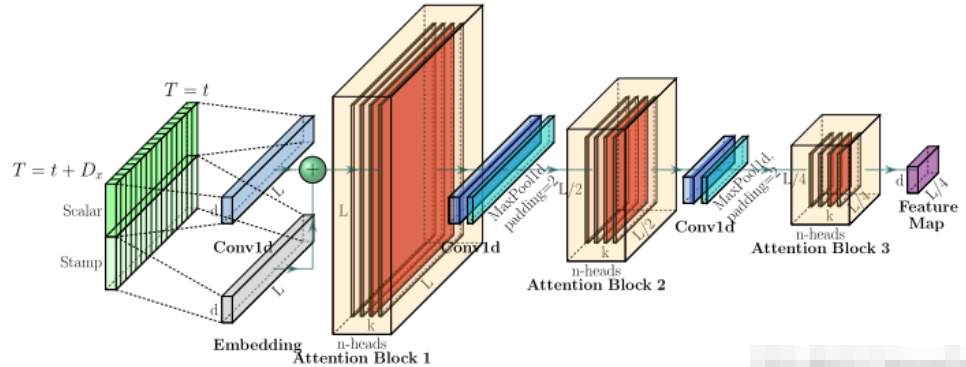
图为:Informer 编码器中的单个堆栈
其中Self-attention Distilling机制的作用表现在每个attention block后加入Cov1d + Maxpooling操作来减少特征维度;Informer在encoder模块用到Self-attention Distilling抽取最重要的Attention信息并减少算法所需的内存和时间。
Informer设计了多个stack副本。(图中只画了一个encoder,实际还上有多个stack),我们先看主序列,其输入是token和时间戳的输入表示(绿色浅的是时间戳,绿色深色的是token),然后输入表示会经过一个卷积层Conv1d(在序列上进行卷积),然后得到大小为L*d的表示(蓝色块以及灰色块)再将两者相加为Attention Block(橙色块)的输入。随后这个表示会经过多个Attention Block,在每一个Attention Block中都有多头ProbSparse Self-Attention(这个多头机制与transformer的机制中的多头机制是一样的)。
每个Block的输出都会依次经过一个Conv1d卷积层,ELU激活层,Maxpooling层。通过Maxpooling层就可以把特征维度减小,这就是Distilling操作,经过多次操作后可以得到最终缩小后的表示Feature Map(紫色块)。这样就可以提高算法的鲁棒性。Infomer还堆叠了多个stack。对于下一个stack,在最开始进行embedding时(蓝色和灰色),通过Conv1d卷积层直接将输入长度减少一半。同时为了保证输出维度相同,第二个stack减少了一个Attention Block。最后,将多个stack得到的Feature Map拼接,得到了Encoder最终的输出。
堆栈这一块具体还不是很懂,待补充~
具体后续可参考:最佳论文-informer[1] 主要思想和代码
1.3.4 一步生成式 Decoder
Informer使用的Decoder和传统的Decoder不同,生成式decoder一次性生成所有的预测输出,而传统的Transformer是将上一步的输出放入decoder在得到下一步的输出,这样每步只能输出一个time step的数据。
这种形式的decoder的start token 是从input中sample一个较短的序列(需要预测的序列的之前一个片断),decoder输入是encoder输入的后面部分的截取+与预测目标形状相同的0矩阵。Decoder需要输入:
在这里插入图片描述
其中, X t o k e n t X_{token}^t Xtokent 为start token序列, X 0 t X_0^t X0t 为需要预测序列,用0填充。
在这里插入图片描述
Decoder构成是由两个DecoderLayer构成,而每个DecoderLayer的内部,还包括:一个mak self-attention;一个multi cross-attention,负责target sequence和source sequence的交互用的;两个conv1,是512 -> 2048 -> 512用的,类似FFN;三个layer norm,一个dropout。(具体如何还需读源代码)
将Masked multi-head attention应用于ProbSparse self-attention,将mask的点积设置为 − ∞ -\infty −∞。它可以防止每个位置都关注未来的位置,从而避免了自回归。
经过Decoder后,每个placeholder(待预测位置)都有一个向量,然后输入到一个全连接层得到预测结果。
1.4 创新点
ProbSparse self-attention
统一输入表示
self-attention蒸馏机制
一步生成式 Decoder
这些独特之处,解决了之前的类Transformer模型的主要三大问题,二次计算复杂度,高耗内存,预测长输出受限。
1.5 小结
Informer与Autoformer的关注点不同,Informer在长时间序列预测中仍然是逐点,都是从self-attention机制的缺陷出发;而Autoformer的模型将从序列分解出发,提出Auto-Correlation机制替代self-attention,其考虑sub-series(子序列)间的相似度能更好的捕捉到趋势性,更多的关注序列。Autoformer模型的预测效果好坏好像取决于特征工程,或者说autoformer抗噪能力还不够,有一些可解释的项代价就是效果不如叠attention,所以一般都认为在实际应用效果往往不如Informer模型预测。(这些其实都需要去自己去应用一遍,比较一下才是最好的),对于Autoformer的代码复现现在还有点困难,将做为后续的一部分工作之一,再来对比这篇Informer模型。
Informer模型仍然待补充~
后续参考补充:
1. 细读informer思考+代码系列解读
二. pytorch 基础
2.1 损失函数与反向传播
先是简单的自定义tensor张量去计算loss:
import torch
from torch.nn import L1Loss
from torch import nn
inputs = torch.tensor([1, 2, 3], dtype=torch.float32) # 自定义的tensor张量, 变成浮点数
targets = torch.tensor([1, 2, 5], dtype=torch.float32)
inputs = torch.reshape(inputs, (1, 1, 1, 3))# input(N,*) 改变input与targets的形状:1个样本,通道为1,宽高为1*3(一行三列)
targets = torch.reshape(targets,(1, 1, 1, 3))
loss = L1Loss() # L1Loss()可以选择计算的方式
result = loss(inputs, targets)
loss_mse = nn.MSELoss( )
result_mse = loss_mse(inputs,targets)
print(result)
print(result_mse)
# 代码的计算过程为 :
# 1-1 = 0, 2-2 = 0,3-5 = -2 , 绝对值相加除以3 = 0.6667
# 若 loss = L1Loss(reduction="sum") 则结果只相加 = 2
x= torch.tensor([0.1,0.2,0.3])
y= torch.tensor([1])
x = torch.reshape(x,(1,3))
loss_cross = nn.CrossEntropyLoss()
result_cross = loss_cross(x,y)
print(result_cross)
我们再将之前简单的神经网络模型直接应用CIFAR10图片数据集的十分类问题中,其中需要注意的是我们应该通过对比outputs与targets之间的关系去选择合适的loss function;比如下面分类图片例子中,根据输出与标签可得应选择CrossEntropyLoss(),并且该交叉熵有两个作用:
计算实际输出与目标之间的差距;
为更新输出提供一点的依据(方向传播),grad
每一个需要更新的参数都需要求出一个对应的梯度,在优化过程中,可根据梯度进行参数优化,达到降低loss的目的。(梯度下降法)
import torch
import torchvision
from torch import nn
from torch.nn import Conv2d,MaxPool2d,Flatten,Linear,Sequential
from torch.utils.data import DataLoader
dataset = torchvision.datasets.CIFAR10("./dataset", train=False, transform=torchvision.transforms.ToTensor(),
download=True)
dataloader = DataLoader(dataset, batch_size=1)
class test(nn.Module):
def __init__(self):
super(test, self).__init__()
#Sequential可以简化代码
self.model1 = nn.Sequential(
nn.Conv2d(3, 32, 5, padding=2, stride=1),
nn.MaxPool2d(2),
nn.Conv2d(32, 32, 5, stride=1, padding=2),
nn.MaxPool2d(2),
nn.Conv2d(32, 64, 5, stride=1, padding=2),
nn.MaxPool2d(2),
nn.Flatten(),
nn.Linear(1024, 64),
nn.Linear(64, 10)
)
def forward(self, x):
x = self.model1(x)
return x
test1=test()
loss=nn.CrossEntropyLoss()
for data in dataloader:
imgs, targets = data
print(imgs.shape)
outputs = test1(imgs)
print(outputs) # outputs为经过VGG模型分类的输出
print(targets) # targets为标签
result_loss = loss(outputs,targets)
print(result_loss)
result_loss.backward()
print("ok")
2.2 优化器
我们之前的做的反向传播具有极大的作用对于训练模型参数,有了模型中各节点的参数梯度,该如何选择合适的优化器来进行参数优化,以达到最低的loss。
import torch
import torchvision
from torch import nn
from torch.nn import Conv2d, MaxPool2d, Flatten, Linear, Sequential
from torch.utils.data import DataLoader
dataset = torchvision.datasets.CIFAR10("./dataset", train=False, transform=torchvision.transforms.ToTensor(),
download=True)
dataloader = DataLoader(dataset, batch_size=1)
class test(nn.Module):
def __init__(self):
super(test, self).__init__()
# Sequential可以简化代码
self.model1 = nn.Sequential(
nn.Conv2d(3, 32, 5, padding=2, stride=1),
nn.MaxPool2d(2),
nn.Conv2d(32, 32, 5, stride=1, padding=2),
nn.MaxPool2d(2),
nn.Conv2d(32, 64, 5, stride=1, padding=2),
nn.MaxPool2d(2),
nn.Flatten(),
nn.Linear(1024, 64),
nn.Linear(64, 10)
)
def forward(self, x):
x = self.model1(x)
return x
test1 = test()
loss = nn.CrossEntropyLoss()
# 设置优化器
optim = torch.optim.SGD(test1.parameters(), lr=0.01)
for epoch in range(20):
running_loss = 0.0
for data in dataloader:
imgs, targets = data
#print(imgs.shape)
outputs = test1(imgs)
#print(outputs) # outputs为经过VGG模型分类的输出
#print(targets) # targets为标签
result_loss = loss(outputs, targets)
optim.zero_grad()
result_loss.backward() # backward 会计算每一个参数节点的梯度
optim.step()
running_loss = running_loss + result_loss
# epoch循环结束之后
print(running_loss)
# Files already downloaded and verified
# tensor(18638.4355, grad_fn=<AddBackward0>)
# tensor(16128.6719, grad_fn=<AddBackward0>)
# 进程已结束,退出代码0
在优化过程中可利用debug操作,观测grad的变化:如下图
在这里插入图片描述
2.3 VGG16模型的使用与修改
利用现有的VGG16模型去添加模型结构,适合去做一个前置的网络结构,可以提取一些特殊的特征,这其实也十分重要!
import torchvision
from torch import nn
# train_data = torchvision.datasets.ImageNet("../dataset",split = 'train',download = True,
# transform=torchvision.transforms.ToTensor())
vgg16_false=torchvision.models.vgg16(pretrained=False)
vgg16_true=torchvision.models.vgg16(pretrained=True) # 模型参数都有训练好的VGG模型
print(vgg16_true)
train_data = torchvision.datasets.CIFAR10("../dataset", train=True, transform=torchvision.transforms.ToTensor(),
download=True)
# 添加
vgg16_true.add_module('add_linear', nn.linear(1000,10))
print(vgg16_true)
# 修改
print(vgg16_false)
vgg16_false.classifier[6] = nn.Linear(4096, 10)
print(vgg16_false)
# 发现有修改
原始的VGG16 模型的网络结构如下图所示:是直接从model里面下载的结构:
在这里插入图片描述
在这里插入图片描述
会发现模型的网络结构发生添加或者修改了。
2.4 完整网络模型的训练套路简单汇总
2.4.1 网络模型的保存与读取
保存方式1: 模型结构+参数(占内存大,不推荐)
保存方式2:模型参数
import torch
import torchvision
from torch import nn
vgg16 = torchvision.models.vgg16(pretrained=False)
# 保存方式1 “保存路径.pth”什么后缀都行推荐为.pth 保存 模型结构+参数
torch.save(vgg16, "vgg16_method1.pth")
# 保存方式2 , 模型参数(官方推荐)
torch.save(vgg16.state_dict(), "vgg16_method2.pth")
#依然是保存方式1:(自定义的模型需要全部引入,才能读取到)
class Test(nn.Module):
def __init__(self):
super(Test, self).__init__()
self.conv1 = nn.Conv2d(3, 64, kernel_size=3) ## 随意的一个操作
def forward(self, x):
x = self.conv1(x)
return x
test = Test()
torch.save(test,"test_method1.pth")
读取方式与保存方式对应:
import torch
from model_save import *
import torchvision
# 保存与读取方式需要对应(方式一),加载方式1:
model = torch.load("vgg16_method1.pth")
# print(model)
# 方式二对应读取方式(官方比较推荐的读取方式)
vgg16 = torchvision.models.vgg16(pretrained=False)
vgg16.load_state_dict(torch.load("vgg16_method2.pth"))
model = torch.load('test_method1.pth')
print(model)
2.4.2 完整模型套路
搭建神经网络,CIFAR10有10个类别,所以要搭建一个10分类的网络:
创建网络模型(model.py要确保与train.py在同一文件夹就行)
import torch
from torch import nn
class Test(nn.Module):
def __init__(self):
super(Test, self).__init__()
# 为了避免上下两个def都写一整串,将整个网络放到序列当中
self.model = nn.Sequential(
# Conv2d(in_channels=3, out_channels=6, kernel_size=3, stride=1, padding=0),按ctrl+p会提示需填写的参数
nn.Conv2d(3, 32, 5, 1, 2), # 卷积
nn.MaxPool2d(2), # 最大池化
nn.Conv2d(32, 32, 5, 1, 2), # 卷积
nn.MaxPool2d(2),
nn.Conv2d(32, 64, 5, 1, 2),
nn.MaxPool2d(2),
nn.Flatten(),
nn.Linear(64*4*4, 64), # 最后两步的展平
nn.Linear(64, 10)
)
def forward(self, x):
x = self.model(x)
return x
# 简单的验证模型是否正确
if __name__ == '__main__':
test = Test()
input = torch.ones((64, 3, 32, 32)) # 创建一个输出的尺寸 64个图片,3个通道,32*32的
output = test(input)
print(output.shape)
训练模型的完整步骤:
import torch
import torchvision
from torch.utils.tensorboard import SummaryWriter
from model import *
from torch import nn
from torch.utils.data import DataLoader
# 训练数据集的下载,root为下载位置
train_data = torchvision.datasets.CIFAR10(root="./dataset", train=True, transform=torchvision.transforms.ToTensor(),
download=True)
# 测试数据集的下载
test_data = torchvision.datasets.CIFAR10(root="./dataset", train=False, transform=torchvision.transforms.ToTensor(),
download=True)
train_data_size = len(test_data)
test_data_size = len(test_data)
# 如果训练数据集的长度train_data_size=10,则会输出 训练数据集的长度为:10
print("训练数据集的长度为:{}".format(train_data_size))
print("测试数据集的长度为:{}".format(test_data_size))
# 利用DataLoader来加载数据集
train_dataloader = DataLoader(train_data, batch_size=64)
test_dataloader = DataLoader(test_data,batch_size=64)
# 创建网络模型(model要确保在同一文件夹就行)
test =Test()
# 创建定义好损失函数
loss_fn = nn.CrossEntropyLoss()
# 定义优化器
learning_rate = 1e-2 # SGD为随机梯度下降优化器,学习速率为learning_rate = 0.01
optimizer = torch.optim.SGD(test.parameters(), lr=learning_rate)
# 设置训练网络的一些参数
# 记录训练的次数
total_train_step = 0
# 记录测试的次数
total_test_step = 0
# 训练的轮数
epoch = 10
# 添加tensorboard的使用
writer = SummaryWriter("logs_train")
for i in range(epoch):
print("------第 {} 轮训练开始------".format(i+1)) # 为了符合阅读习惯,写成i+1 (i从0取到9)
# 训练步骤开始
for data in train_dataloader:
imgs, targets = data
outputs = test(imgs)
loss = loss_fn(outputs, targets) # 输出和目标之间的损失值
# 优化器调优 优化模型
optimizer.zero_grad() # 优化前梯度清零
loss.backward() # 调用损失的反向传播,得到每个参数检验的梯度
optimizer.step()# 调用优化器,进行了一次训练,完成一次优化
# 一次训练完成,训练次数+1
total_train_step = total_train_step + 1
#只显示100能够整除的信息
if total_train_step %100 == 0:
# 因为有两个{}需要替换,所以format有两个量去替换大括号中的值
print("训练次数: {},Loss: {}".format(total_train_step, loss.item()))
writer.add_scalar("train_loss",loss.item(),total_train_step) # 添加tensorboard
# 测试步骤开始
total_test_loss = 0
with torch.no_grad():
for data in test_dataloader:
imgs,targets =data
outputs = test(imgs)
loss = loss_fn(outputs,targets)
total_test_loss = total_test_loss + loss.item()
print("整体测试集上的Loss:{}",format(total_test_loss))
writer.add_scalar("test_loss",total_test_loss,total_test_step) # 添加tensorboard
total_test_step = total_test_step + 1
# 保存训练模型的每一轮
torch.save(test,"test_{}.pth".format(i))
print("模型已保存!")
writer.close()
并在tensorboard上面展示模型训练LOSS下降的过程:
在终端中输入:tensorboard --logdir=logs_train
在这里插入图片描述
在这里插入图片描述
对分类问题特有的衡量指标-正确率的理解与应用
import torch
# 假设的二分类问题
outputs = torch.tensor([[0.1, 0.2],
[0.3, 0.4]])
test_len=10 # 测试集长度
print(outputs.argmax(1)) # 按横向取出最大的值
preds = outputs.argmax(1) # preds取最大值的位置
targets = torch.tensor([0, 1])
print(preds ==targets)
print((preds ==targets).sum()) # 计算为true的个数
print(((preds ==targets).sum())/test_len)
#tensor([1, 1])
#tensor([False, True])
#tensor(1)
#tensor(0.1000)
将正确率应用到上面的模型中:
# 测试步骤开始
total_test_loss = 0
total_accuary =0
with torch.no_grad():
for data in test_dataloader:
imgs,targets =data
outputs = test(imgs)
loss = loss_fn(outputs,targets)
total_test_loss = total_test_loss + loss.item()
accuary = (outputs.argmax(1) ==targets).sum()
total_accuary =total_accuary +accuary
print("整体测试集上的Loss:{}",format(total_test_loss))
print("整体测试集上的正确率:{}".format(total_accuary/test_data_size))
writer.add_scalar("test_loss",total_test_loss,total_test_step) # 添加tensorboard
writer.add_scalar("test_accuacy",total_accuary/test_data_size,total_test_step)
total_test_step = total_test_step + 1
在这里插入图片描述
————————————————
版权声明:本文为CSDN博主「HSR CatcousCherishes」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_44790306/article/details/124064177


 浙公网安备 33010602011771号
浙公网安备 33010602011771号