嵌入与表示学习 embedding & representation learning, embedding & Encoding
视频:
https://www.bilibili.com/video/BV1Cf4y1e7Ht/?spm_id_from=333.788&vd_source=6292df769fba3b00eb2ff1859b99d79e
==========================================
Embedding
Embedding 是一个将离散变量转为连续向量表示的一个方式。在神经网络中,embedding 是非常有用的,因为它不光可以减少离散变量的空间维数,同时还可以有意义的表示该变量。
我们可以总结一下,embedding 有以下 3 个主要目的:
- 在 embedding 空间中查找最近邻,这可以很好的用于根据用户的兴趣来进行推荐。
- 作为监督性学习任务的输入。
- 用于可视化不同离散变量之间的关系。
以下(以上)内容来自(参考): https://zhuanlan.zhihu.com/p/46016518
==========================================
Embedding
简单来说,Embedding 就是用一个低维的向量表示一个物体,可以是一个词,或是一个商品,或是一个电影等等。这个embedding向量的性质是能使距离相近的向量对应的物体有相近的含义,比如 Embedding(复仇者联盟)和Embedding(钢铁侠)之间的距离就会很接近,但 Embedding(复仇者联盟)和Embedding(乱世佳人)的距离就会远一些。
除此之外Embedding甚至还具有数学运算的关系,比如Embedding(马德里)-Embedding(西班牙)+Embedding(法国)≈Embedding(巴黎)
以下(以上)内容来自(参考): https://zhuanlan.zhihu.com/p/53194407
==========================================
什么是表示?
为了提高机器学习系统的准确率,我们需要将输入信息转换为有效的特征,这就是:表示。一般而言,一个好的表示具有以下几个优点:
- 一个好的表示应该具有很强的表示能力,即同样大小的向量可以表示更多信息。
- 一个好的表示应该使后续的学习任务变得简单,即需要包含更高层的语义信息。
- 一个好的表示应该具有一般性,是任务或领域独立的。虽然目前的大部分 表示学习方法还是基于某个任务来学习,但我们期望其学到的表示可以比较容易地迁移到其他任务上。
局部表示和分布式表示?
以颜色表示为例 ,如果要在计算机中表示颜色,局部表示的方法是以不同名字来命名不同的颜色,也称为离散表示或符号表示。局部表示通常可以表示为one-hot向量形式。one-hot向量为有且只有一个元素为 1,其余元素都为0的向量。另一种表示颜色的方法是用 RGB 值来表示颜色,不同颜色对应到 R、G、B 三 维空间中一个点,这种表示方式叫做分布式表示。分布式表示叫做分散式表示可能更容易理解,即一种颜色的语义分散到语义空间中的不同基向量上。分布式表示通常可以表示为低维的稠密向量。
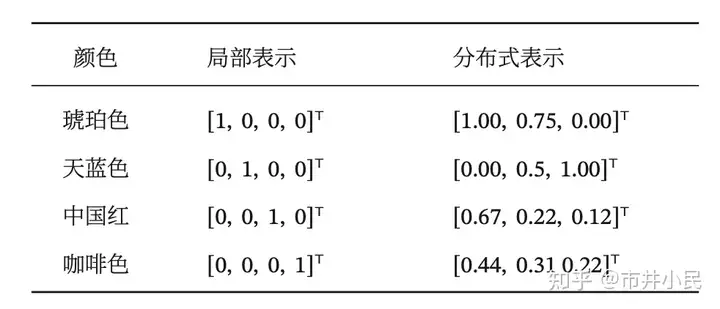
颜色的表示
局部表示优点:
- 这种离散的表示方式具有很好的解释性,有利于人工归纳和总结特征,并通过特征组合进行高效的特征工程。
- 通过多种特征组合得到的表示向量通常是稀疏的二值向量,当用于线性模型时计算效率非常 高。
局部表示不足:
- one-hot 向量的维数很高且不能扩展。如果有一种新的颜色,我们就需要增加一维来表示。
- 不同颜色之间的相似度都为0(所以基向量都是正交的),即我们无法知道“红色”和“中国红”的相似度要高于“红色”和“黑色”的相似度。
分布式表示改进:
- 分布式表示的向量维度一般都比较低。我们只需要用一个三维的稠密向量就可以表示所有颜色。
- 分布式表示也很容易表示新的颜色名。
- 不同颜色之间的相似度也很容易计算。

以下(以上)内容来自(参考): https://zhuanlan.zhihu.com/p/379709761
==========================================
"token", "embedding","encoding"各自的区别
token:模型输入基本单元。比如中文BERT中,token可以是一个字,也可以是<CLS>等标识符。
embedding:一个用来表示token的稠密的向量。token本身不可计算,需要将其映射到一个连续向量空间,才可以进行后续运算,这个映射的结果就是该token对应的embedding。
encoding:表示编码的过程。将一个句子,浓缩成为一个稠密向量(也称为表征, representation),这个向量可以用于后续计算,用来表示该句子在连续向量空间中的一个点。理想的encoding能使语义相似的句子被映射到相近的空间。
以下(以上)内容来自(参考):https://www.zhihu.com/question/500600126/answer/2237165857
==========================================
Embedding & Encoding 区别:
position embedding和position encoding是什么?有什么区别?
通常,embedding是指学习出来的encoding,是将位置信息“嵌入”到某个空间的意思。例如,bert的位置编码是学出来的,所以称为position embedding。
而transformer的位置编码是用三角函数直接算出来的(当然,论文中说也可以学出来,效果差不多,所以最后还是采用了直接编码),不涉及嵌入的思想,所以叫position encoding。
虽然position embedding和position encoding从翻译的角度意思类似,但是在位置表征中含义是不一样的。
为什么要做position embedding或是encoding?因为用Attention或CNN代替RNN机制之后,单词失去了位置信息,以至于“我爱你“和“你爱我“在Attention机制的视野里完全一样。所以需要某种方法将位置信息编码进语义表征中。
position embedding 在 Convolutional Sequence to Sequence Learning 定义。大意就是(x0, x1, x2, ...)token序列经过embedding矩阵变成(w0, w1, w2, ...)的词向量序列,同时(0,1,2,...)的绝对位置序列也经过另一个embedding矩阵变为(p0,p1,p2,...)。最终的embedding序列就是 e = (x0+p0, x1+p1, x2+p2, ...)。位置embeding矩阵靠训练学习获得。
position encoding 是 Attention is all you need 中使用。
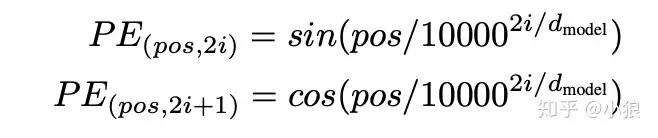
使用上图这样纯数学的方式处理word embdding,大概的思路就是:“相近的词影响更大“。
以下(以上)内容来自(参考):https://www.zhihu.com/question/402387099/answer/1313986225
Embedding & Encoding 区别:
区别:Position Embedding是学习式,Position Encoding是固定式
Transformer的结构是基于Self-Attention的,与RNN/CNN不同,不包含序列信息,但是序列信息又极其重要,为了融合序列信息,就需要位置编码了
Transformer的论文提出了两种编码方式:学习式和固定式
学习式
定义:当做可训练参数随机初始化,比如最长512,编码维度768,则随机初始化一个512x768矩阵,让其随训练进行更新,目前的BERT、GPT等预训练模型都是通过这种方式获得位置编码
缺点:不可扩展,即如果预训练最大长度为512,则最多能处理512长度的句子
固定式
通过公式直接计算,例如Transformer通过三角函数直接计算得到
使用周期函数表示位置编码有两个理由,一个是参考二进制,二是可以轻松学到相对位置(任意位置的编码都可以通过前面某个位置编码的线性表示得到,可以通过cos加法和sin加法规则证明,这也是PE同时使用cos和sin的原因)
三角函数中使用10000的原因,确保循环周期足够大,以便于编码足够长的文本(其实就是这样做实验效果更好)
以下(以上)内容来自(参考): https://www.cnblogs.com/WMT-Azura/p/16666660.html
==========================================
Embedding & Encoding 区别:
经常会遇到embedding的概念,要搞清楚embeding先要弄明白他和one hot encoding的区别,以及他解决了什么one hot encoding不能解决的问题。
独热编码(One-hot encoding)向量是高维且稀疏的。假如说我们在做自然语言处理(NLP)的工作,并且有一个包含 2000 个单词的字典。这意味着当我们使用独热编码时,每个单词由一个含有 2000 个整数的向量来表示,并且其中的 1999 个整数都是 0。在大数据集下这种方法的计算效率是很低的。
但是one-hot编码的优势在于,计算方便快捷、表达能力强。
有没有一种办法将独热编码转换一下,化稀疏为密集,提高其效率?这个转换过程就是embedding,嵌套!最开始主要是应用在nlp自然语言处理中的。正如Keras 文档里是这么写embedding的:“把正整数(索引)转换为固定大小的稠密向量”。
转换方法可类比下面(实际上就是个转换函数,可以有很多其他方式):
直观上就可以发现,编码矩阵已经减小了一半了!
达到了“降维”的效果。而其中转换的矩阵,可以理解为转换表,过渡矩阵。
以下(以上)内容来自(参考):
http://blog.leanote.com/post/lee-romantic/6c8866416d54
==========================================


 浙公网安备 33010602011771号
浙公网安备 33010602011771号