Keras compile loss metrics

The purpose of loss functions is to compute the quantity that a model should seek to minimize during training.

 

https://tensorflow.google.cn/api_docs/python/tf/keras/metrics

A metric is a function that is used to judge the performance of your model.
Metric functions are similar to loss functions, except that the results from evaluating a metric are not used when training the model. Note that you may use any loss function as a metric.

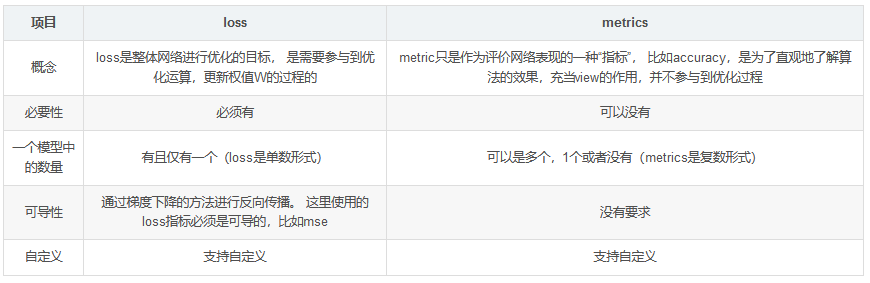
loss与metrics对比理解 

 

 

loss常用方法

参考自：https://keras.io/zh/losses/
更多细节参考：https://keras.io/api/losses/

连续型：
mean_squared_error 或 mse
mean_absolute_error 或 mae
mean_absolute_percentage_error 或 mape
mean_squared_logarithmic_error 或 msle
squared_hinge
hinge
categorical_hinge
logcosh 预测误差的双曲余弦的对数。

类别型：
categorical_crossentropy： 亦称作多类的对数损失，注意使用该目标函数时，需要将标签转化为形如(nb_samples, nb_classes)的二值序列
sparse_categorical_crossentropy
binary_crossentropy （亦称作对数损失，logloss）
kullback_leibler_divergence
poisson
cosine_proximity 即预测值与真实标签的余弦距离平均值的相反数

keras.Sequential.compile(loss='目标函数 ', optimizer=‘adam’, metrics=[‘accuracy’])

 

metrics常用方法

中文：https://keras.io/zh/metrics/
英文：https://keras.io/api/metrics/

binary_accuracy
categorical_accuracy
sparse_categorical_accuracy
top_k_categorical_accuracy
sparse_top_k_categorical_accuracy
自定义评价函数

 

使用方法

compile方法中的使用

# 方法1
model.compile(loss='mean_squared_error',
              optimizer='sgd',
              metrics=['mae', 'acc'])

# 方法2
from keras import metrics
model.compile(loss='mean_squared_error',
              optimizer='sgd',
              metrics=[metrics.mae, metrics.categorical_accuracy])

 

5、参考资料

官网资料
英文：https://keras.io/api/losses/
英文：https://keras.io/api/metrics/

中文：https://keras.io/zh/losses/
中文：https://keras.io/zh/metrics/
————————————————
链接：https://blog.csdn.net/chenhepg/article/details/115721826

 

===================================================================

https://blog.csdn.net/zhenyu_qiu/article/details/118069458

https://tensorflow.google.cn/api_docs/python/tf/keras/metrics/CategoricalCrossentropy

===================================================================

 

===================================================================