批标准化 (Batch Normalization)

 

2015年深度学习领域非常棒的一篇文献：《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》，这个算法目前已经被大量的应用，最新的文献算法很多都会引用这个算法，进行网络训练。BN的优点是：

• 可以选择比较大的初始学习率，加快网络的收敛。实验结果表明，就算你使用小的学习率，收敛速度也会很快。
• 减少正则化参数的Dropout、L2正则项参数的选择问题，BN具有提高网络泛化能力的特性。
• 不需要使用局部响应归一化层（局部响应归一化是Alexnet网络用到的方法），因为BN本身就是一个归一化网络层。
• 可以把训练数据彻底打乱，防止每批训练的时候，某一个样本经常被挑选到，在ImageNet上提高1%的精度。

BN的核心思想不是为了防止梯度消失或者防止过拟合，其核心是通过对系统参数搜索空间进行约束来增加系统鲁棒性，这种约束压缩了搜索空间，约束也改善了系统的结构合理性，这会带来一系列的性能改善，比如加速收敛，保证梯度，缓解过拟合等。

 

 

 

 

 

 

 

归一化（normalization）
将一批不太标准的数据统一到指定的格式.
我们在数据处理时常用的是将一组范围差距较大或者单位不同的数据依据一定规则变化到指定的范围之内。

Batch_normalization

BN来源：
有之前的工作说明对图像的像素值分布变换为以0为均值，单位方差的正态分布数值时(这种操作被称为whiten)，可以加速网络收敛。现在换作深度神经网络每一隐藏层的输入也可以做whiten吧？这样BN出现了。
 
BN原因：
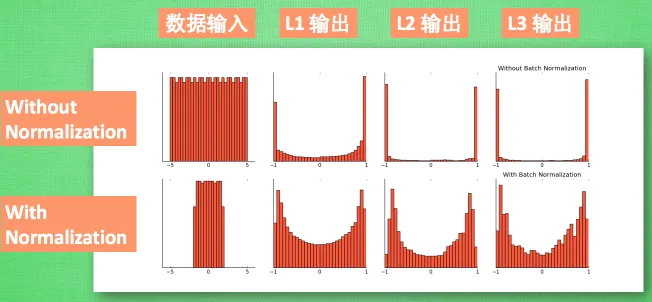
随着网络的深度增加，每层特征值分布会逐渐的向激活函数的输出区间的上下两端（激活函数饱和区间）靠近，这样继续下去就会导致梯度消失。BN就是通过方法将该层特征值分布重新拉回标准正态分布，特征值将落在激活函数对于输入较为敏感的区间，输入的小变化可导致损失函数较大的变化，使得梯度变大，避免梯度消失，同时也可加快收敛。

具体形象理解可以查看：https://www.cnblogs.com/guoyaohua/p/8724433.html

 
BN做法：
https://images2018.cnblogs.com/blog/1192699/201804/1192699-20180405213955224-1791925244.png
上图来自https://www.cnblogs.com/guoyaohua/p/8724433.html

位于Y = weight*X+Bias之后，激活函数（非线性函数）变换之前，即作用在Y上，作为激活函数输入。
过程：input={x1,x2,x3…xn}
1 计算 x1-xn的均值u
2 计算x1-xn的方差v
3 每个x_i = (x_i – u) / (sqrt(v^2)+ e)  e是一个小小偏置，防止分母趋向于0.
4 在对结果进行scale于shift操作 x_i = scale*x_i + shift
第四步存在的原因是batch_normal后，数据趋向标准正态，会导致网络表达能力变差，这里加入后标准正态分布有些偏移，变得不那么标准了。这两个参数时学习而来。

 
BN优缺点：
减少梯度消失，加快了收敛过程。
起到类似dropout一样的正则化能力，一定程度上防止过拟合。
放宽了一定的调参要求。
可以替代LRN。

但是需要计算均值与方差，不适合动态网络或者RNN。计算均值方差依赖每批次，因此数据最好足够打乱。

LRN
为什么要有LRN 局部响应归一化？
https://blog.csdn.net/hduxiejun/article/details/70570086
在神经生物学有一概念叫 “侧抑制”，指的是被激活的神经元会抑制相邻的神经元。
局部响应归一化借鉴了“侧抑制”的思想来实现局部抑制，对局部神经元的活动创建竞争机制，使得相应比较大的值相对大，小的更小。
 
优点：
可提高模型泛化能力，当使用Relu时这种“侧抑制”的方法很管用。
 
LRN公式 ：
https://img-blog.csdn.net/20170424101327406?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvaGR1eGllanVu/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast

a 是第i个核（特征通道）在特征图（x,y）处的输出，在这里作为公式输入。

b 是第i个核（特征通道）在特征图（x,y）处经过LRN后的输出，在这里作为公式输出。

N是通道数（特征图最后一维）。

n是你想要局部抑制的特征通道维数。

K,α，β是超参数。

举个例子：

I =6, (x,y) =(2,2) ,N=10, n=4，a = [w,h,N], k = 2, α=1*e-4, β=0.75

则 n/2 = 2  i+n/2 =8,  i-n/2=4

那么公式就完成在a[2,2,6]处的值除以（“上述公式括号里的值”），而括号里的是

关于【在i通道处，同样位于（x,y）处的第 4，5，6，7，8通道值的平方和】的变换式子，

这里称为式子，因为其中的超参数即是变换式子的变换方法。

 

使用：Tensorflow 提供了函数 tf.nn.lrn()来完成这个操作。

 
Ref:
DeepLearning-500-questions 深度学习基础3.6节

https://github.com/scutan90/DeepLearning-500-questions/blob/master/ch03_%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E5%9F%BA%E7%A1%80/%E7%AC%AC%E4%B8%89%E7%AB%A0_%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E5%9F%BA%E7%A1%80.md

 

【深度学习】深入理解Batch Normalization批标准化

https://www.cnblogs.com/guoyaohua/p/8724433.html
 

深度学习的局部响应归一化LRN(Local Response Normalization)理解

https://blog.csdn.net/yangdashi888/article/details/77918311

 

tensorflow下的局部响应归一化函数tf.nn.lrn

https://blog.csdn.net/sinat_21585785/article/details/75087768
————————————————

 

链接：https://blog.csdn.net/hffhjh111/article/details/86994445

 

 

https://zhuanlan.zhihu.com/p/24810318

https://zhuanlan.zhihu.com/p/435507061

https://blog.csdn.net/hffhjh111/article/details/86994445

https://github.com/d2l-ai/berkeley-stat-157/tree/master/slides-zh