信息熵 交叉熵 交叉熵误差 条件熵 联合熵 互信息

信息熵

熵定义为信息的期望，某个待分类事物可以划分为多个类别，其中类别的信息为(为的概率)：

熵为所有类别的信息期望值：

 

交叉熵

交叉熵误差：

为实际的分类结果， 为预测的结果，（ 并且   ）

 

 

交叉熵误差

它有三个很好的性质：

1. 它可以真实的反应出真实分类结果和预测结果的误差

预测结果和真实分类结果越接近，误差越接近， 即误差越小

 

2. 交叉熵误差函数和softmax（神经网络用到的输出函数）和sigmoid函数（logistic回归用到的函数）的复合函数是凸函数，即存在全局最优解

凸函数的充要条件是：如果二阶导数存在，二阶到大于

 

3. 在用梯度下降发求解最优解时，需要用到一阶导数，从上面可以看到一阶导数：

 

很简洁，可以简化整个求解过程。

 

互信息：

https://www.cnblogs.com/emanlee/p/12492561.html

https://blog.csdn.net/weixin_42258608/article/details/88059252

 

=============================

1、信息熵H(X)
定义：一个离散随机变量X的熵H(X)定义为

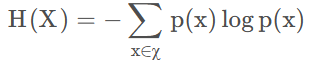
 2、联合熵H(X,Y)
定义：对于服从联合分布为p(x,y)的一对离散随机变量(X,Y)，其联合熵H(X,Y) (joint entropy)定义为：

 
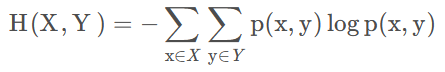
3、互信息I(X,Y)
定义：考虑两个随机变量X和Y，他们的联合概率密度函数为p(x,y)，其边际概率密度函数分别为p(x)和p(y)。互信息I(X;Y)为联合分布p(x,y)和p(x)p(y)之间的相对熵，即：

 
4、条件熵H(X|Y)
定义：若（X，Y)~p(x,y)，条件熵(Conditional entropy) H(Y|X)定义为：

 
————————————————
链接：https://blog.csdn.net/tangxianyu/article/details/105759989