协方差矩阵

 

概念

协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。
其实简单来讲，协方差就是衡量两个变量相关性的变量。当协方差为正时，两个变量呈正相关关系（同增同减）；当协方差为负时，两个变量呈负相关关系（一增一减）。
而协方差矩阵，只是将所有变量的协方差关系用矩阵的形式表现出来而已。通过矩阵这一工具，可以更方便地进行数学运算。

概率统计里面关于方差的数学定义：

 

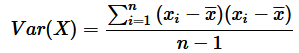
 协方差的数学定义：

 

 这里的X,Y表示两个变量空间。用机器学习的话讲，就是样本有X，Y两种特征，而X 就是包含所有样本的x 特征的集合，Y就是包含所有样本的y特征的集合。

 两个变量的协方差矩阵

假设我们有 4 个样本，每个样本都有两个变量，也就是两个特征，它们表示如下：

 

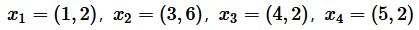
 用一个矩阵表示为：

 

 现在，我们用两个变量空间X，Y 来表示这两个特征：

 

 由于协方差反应的是两个变量之间的相关性，因此，协方差矩阵表示的是所有变量之间两两相关的关系，具体来讲，一个包含两个特征的矩阵，其协方差矩阵应该有2*2大小：

 

 

 

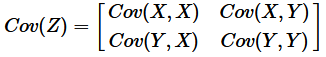
求特征协方差矩阵，如果数据是3维，那么协方差矩阵是

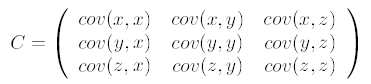
 这里只有x和y，求解得

 对角线上分别是x和y的方差，非对角线上是协方差。协方差大于0表示x和y若有一个增，另一个也增；小于0表示一个增，一个减；协方差为0时，两者独立。协方差绝对值越大，两者对彼此的影响越大，反之越小。

 

协方差矩阵的作用

作为一种数学工具，协方差矩阵经常被用来计算特征之间的某种联系。在机器学习的论文中，协方差矩阵的出现概率还是很高的，用于降维的主成分分析法（PCA）就用到了协方差矩阵。

 

===================================

 协方差矩阵在统计学和机器学习中随处可见，一般而言，可视作方差和协方差两部分组成，即方差构成了对角线上的元素，协方差构成了非对角线上的元素。

 在统计学中，方差是用来度量单个随机变量的离散程度，而协方差则一般用来刻画两个随机变量的相似程度

 其中，方差的计算公式为

 

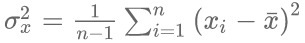
 其中， n表示样本量，符号x-bar表示观测样本的均值。

在此基础上，协方差的计算公式被定义为

 

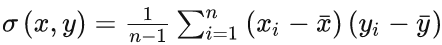
 在公式中，符号x-bar, y-bar分别表示两个随机变量所对应的观测样本均值，据此，我们发现：方差 可视作随机变量 关于其自身的协方差 .

 

===================================

 协方差矩阵定义了数据的离散程度(方差)和空间分布走向(协方差)。

 

 也就是说，协方差矩阵特征分解后的特征向量，总是指向数据最大方差的方向，并规定了其走向。而且由于旋转矩阵的正交性，次最大特征值对应的特征向量，总是与最大特征值的特征向量正交。

 

数据的协方差矩阵，直接与数据的线性变换有关，该线性变换完全由特征向量和特征值定义，特征向量表示了矩阵的旋转，特征值对应各个维度上的缩放因子的平方。

===================================

http://www.ab126.com/shuxue/2788.html    协方差的在线计算器

 

===================================

REF

https://www.cnblogs.com/jermmyhsu/p/8195588.html

https://zhuanlan.zhihu.com/p/37609917

https://zhuanlan.zhihu.com/p/338335181?ivk_sa=1024320u