逆变换采样

逆变换采样（英语：inverse transform sampling），又称为逆采样（inversion sampling）、逆概率积分变换（inverse probability integral transform）、逆变换法（inverse transformation method）、斯米尔诺夫变换（Smirnov transform）、黄金法则（golden rule）等，是伪随机数采样的一种基本方法。在已知任意概率分布的累积分布函数时，可用于从该分布中生成随机样本。

 

 

 

 

 

 

 

 

 

 

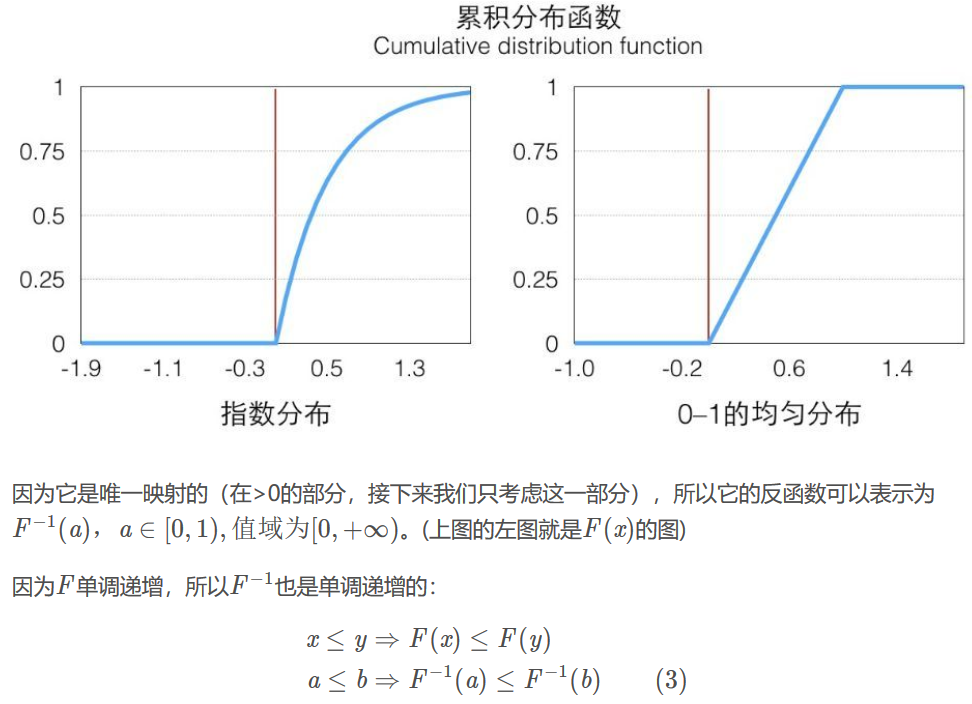
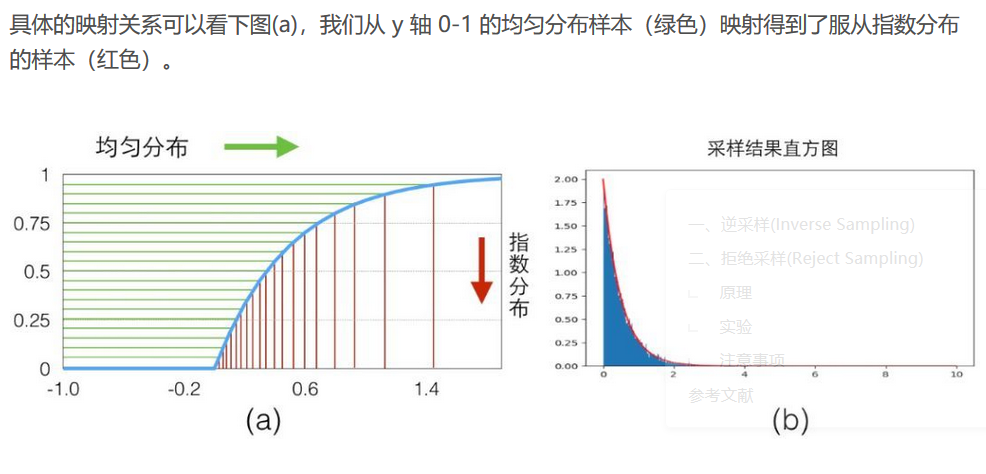
import numpy as np
import matplotlib.pyplot as plt

def sampleExp(Lambda = 2,maxCnt = 50000):
    ys = []
    standardXaxis = []
    standardExp = []
    for i in range(maxCnt):
        u = np.random.random()
        y = -1/Lambda*np.log(1-u) #F-1(X)
        ys.append(y)
    for i in range(1000):
        t = Lambda * np.exp(-Lambda*i/100)
        standardXaxis.append(i/100)
        standardExp.append(t)
    plt.plot(standardXaxis,standardExp,'r')
    #plt.hist(ys,1000,normed=True) # python 2
    plt.hist(ys,1000,density=True) # python 3
    plt.show()

sampleExp()

————————————————

 

 

 

 

 

 

 

 

 

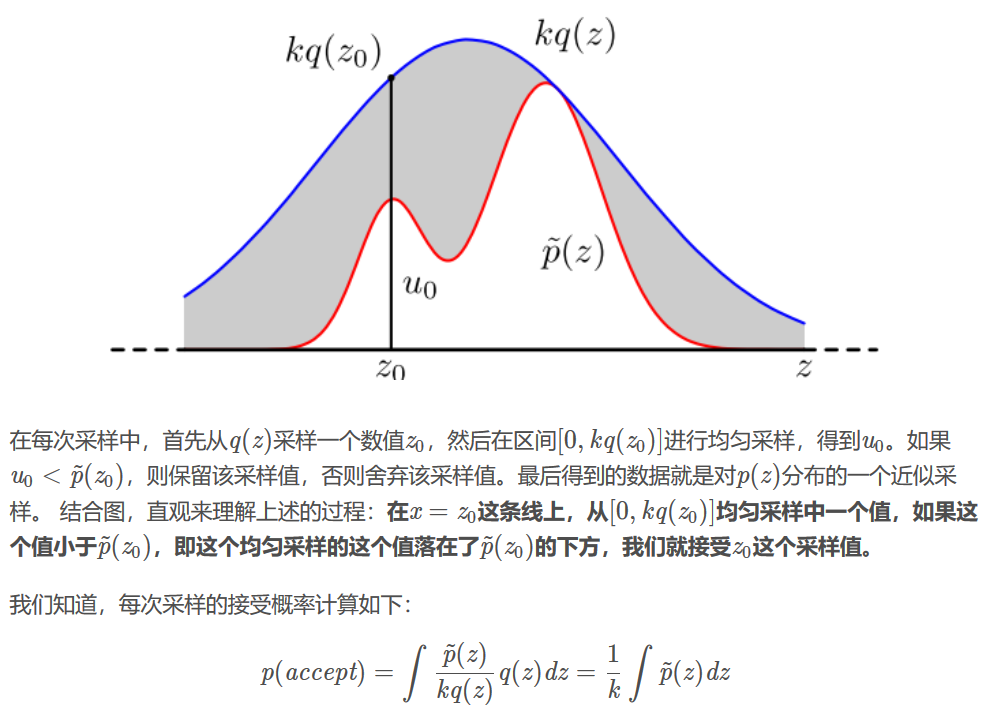
import numpy as np
import matplotlib.pyplot as plt

def f1(x):
    return (0.3*np.exp(-(x-0.3)**2) + 0.7* np.exp(-(x-2.)**2/0.3))/1.2113
x = np.arange(-4.,6.,0.01)
plt.plot(x,f1(x),color = "red")

size = int(1e+07)
sigma = 1.2
z = np.random.normal(loc = 1.4,scale = sigma, size = size)
qz = 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-0.5*(z-1.4)**2/sigma**2)
k = 2.5
#z = np.random.uniform(low = -4, high = 6, size = size)
#qz = 0.1
#k = 10
u = np.random.uniform(low = 0, high = k*qz, size = size)

pz =  0.3*np.exp(-(z-0.3)**2) + 0.7* np.exp(-(z-2.)**2/0.3)
sample = z[pz >= u]
#plt.hist(sample,bins=150, normed=True, edgecolor='black') # python 2
plt.hist(sample,bins=150, density=True, edgecolor='black') # python 3
plt.show()

 

————————————————

 

 

 

 

 

 

 

 

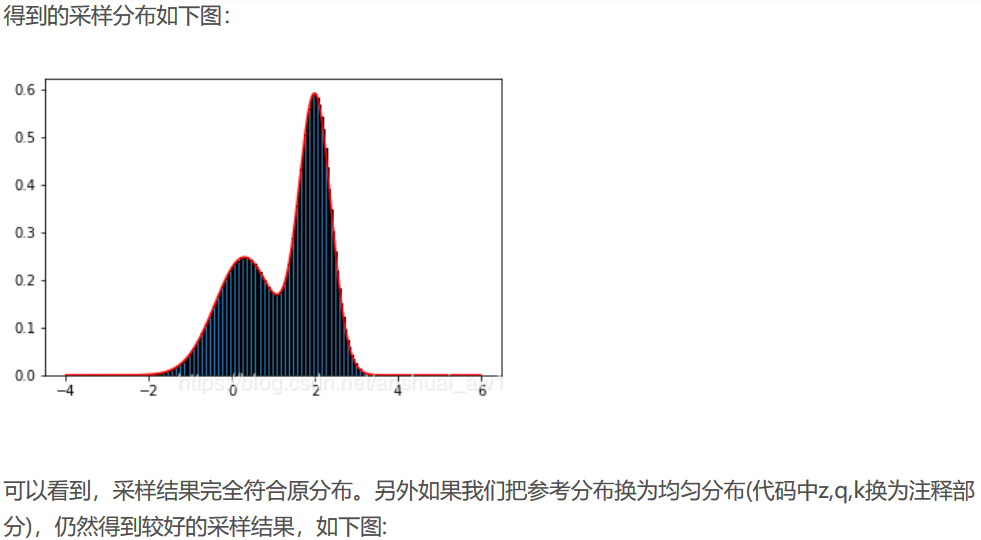
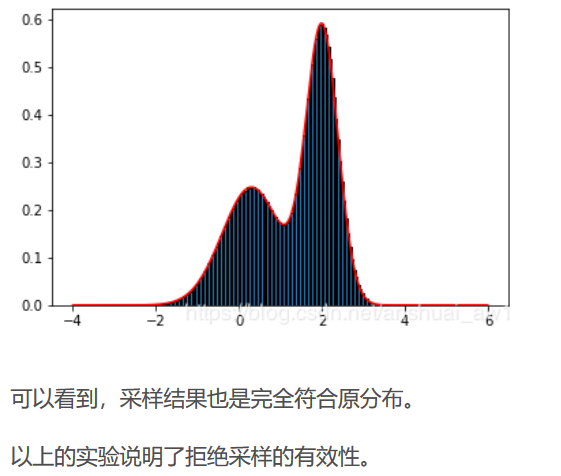
Inverse transform sampling反变换采样法

https://blog.csdn.net/eric2016_lv/article/details/81191430

 

（Good）逆采样(Inverse Sampling)和拒绝采样(Reject Sampling)原理详解

https://blog.csdn.net/anshuai_aw1/article/details/84840446

 

逆变换采样

https://baike.baidu.com/item/%E9%80%86%E5%8F%98%E6%8D%A2%E9%87%87%E6%A0%B7/22934385?fr=aladdin

参考文献

【1】拒绝采样(reject sampling)原理详解

【2】采样方法（一）

【3】蒙特卡洛采样之拒绝采样（Reject Sampling）

【4】一文了解采样方法